文章目录
- 引言:
- 第一题:根据二叉树创建字符串
- 第二题:二叉树的层序遍历
- 第三题:自底向上实现层序遍历
- 第四题:二叉树的最近公共祖先
- 第五题:将搜索二叉树转换成双向链表
- 第六题:从前序和中序遍历序列构造二叉树
- 第七题:二叉树的前序遍历(非递归)
- 第八题:二叉树的中序遍历(非递归)
- 第九题:二叉树的后序遍历(非递归)
- 总结:二叉树有关的OJ题So,So啦!
引言:
北京时间:2023/5/7/8:13,还是那句话,周末不摆烂,从我做起,昨日突下大雨,狂风呼啸,大雨倾盆,雷声隆隆,但依然没有打扰到我的美梦,睡的要多香就有多香,虽然现在依然很困,哈哈哈!也许是我自认为自己睡得很香,哈哈哈,今天有羽毛球打算,但是具体还得看情况,所以该篇博客大致是更不了啦!曾经我好像看到过一句话,就是说大学最重要的就是学习和锻炼,所以羽毛球其实是合理且实用的,哈哈哈,对了,在此博客记录一件事情,昨天五一补课,舍友让我8点去帮其签到(日语课),然后A我20元,对于有一丝丝自律的我来说,小意思啦!肯定不是因为钱,相信我,哈哈哈,然后一切都在计划之中,毕竟我可是非常靠谱的嘛,然而最终,天命不饶人,那个日语老师平常并不提问人,但独独就是这节课,她通过随机选人的方式,一发入魂,剩下懂的都懂,具体为什么我会知道,原因就是我在签到软件上看到随机选人的时候,可能是出于做事要有售后服务,所以我就很好奇的点进去看了一下,想看一下我们这次的计划是否能够天衣无缝,毕竟只有这样,我的20元才能拿的心安理得,不曾想,天命如此,哈哈哈!ok,记录完该事,进入正题,今天就让我们来学习一下和二叉树有关的OJ题,干就完了,小小二叉树,小小递归,就不信我们递不明白,So,here we go!

北京时间:5/14/17:24,可以看出该篇博客的引言我们早都写好了,之所以之前没写,而是留到今天写,原因很简单,因为我把时间都用去搞AVL树和红黑树等相关知识了,到今天AVL树和红黑树相关知识我们算是搞定的差不多了,没写博客之前应该搞定90%,写了博客之后少说95%,但是我知道随着时间的流逝,慢慢的会淡忘掉部分内容,但是不怕,咱有博客作为坚强的后盾,给我们复习,所以AVL树和红黑树的知识就这样吧!今天我们一定要把有关二叉树题目的博客写完,明天学习map和set的封装实现,所以接下来就让我们一起来看看二叉树的几个经典题目吧!
第一题:根据二叉树创建字符串
详细题目:给你二叉树的根结点root,请你采用前序遍历的方式,将二叉树转化为一个由括号和整数组成的字符串,返回构造出的字符串(递归一次就需要加上一个括号),且空结点使用一对空括号"()"表示,转化后需要省略所有不影响字符串与原始二叉树之间的一对一映射关系的空括号对
示例一:

但是注意:如果左为空,右不为空,此时递归左孩子时,空括号不允许省略,因为如果省略了,就无法区分结点到底是左边还是右边了,具体如下图所示:
示例二:
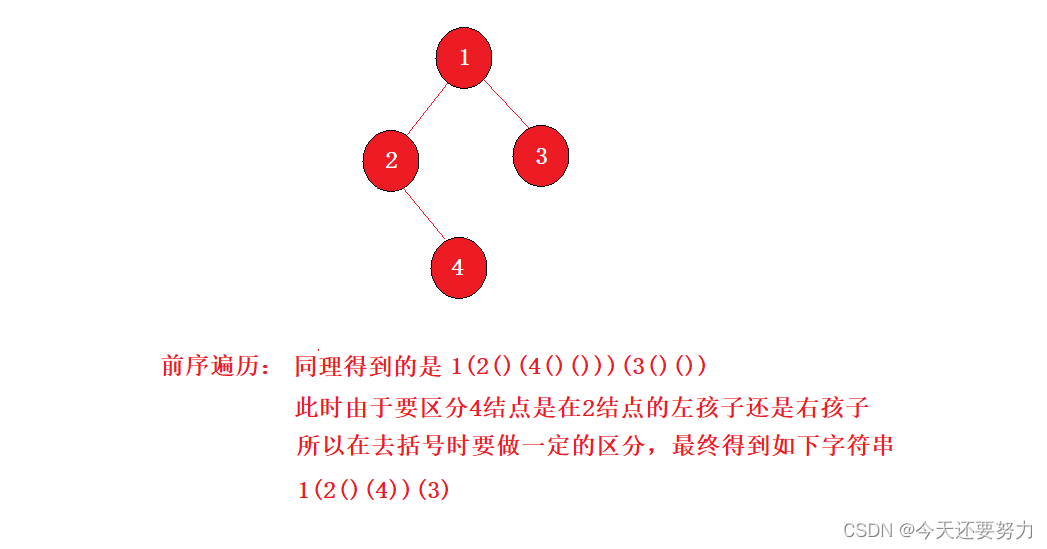
所以此时通过我们对示例的分析,此时我们得出结论:
1.当右结点不为空,左结点为空,此时递归时,空括号不能省略
2.当右结点为空,左结点不为空,此时递归时,空括号需要省略
3.左结点为空,右结点也为空,此时递归时,空括号需要省略
总:也就是说明,当左结点为空,空括号需不需要省略,完全由右结点决定,右结点如果为空,那么省略,右结点如果不为空,那么不省略
具体代码如下:
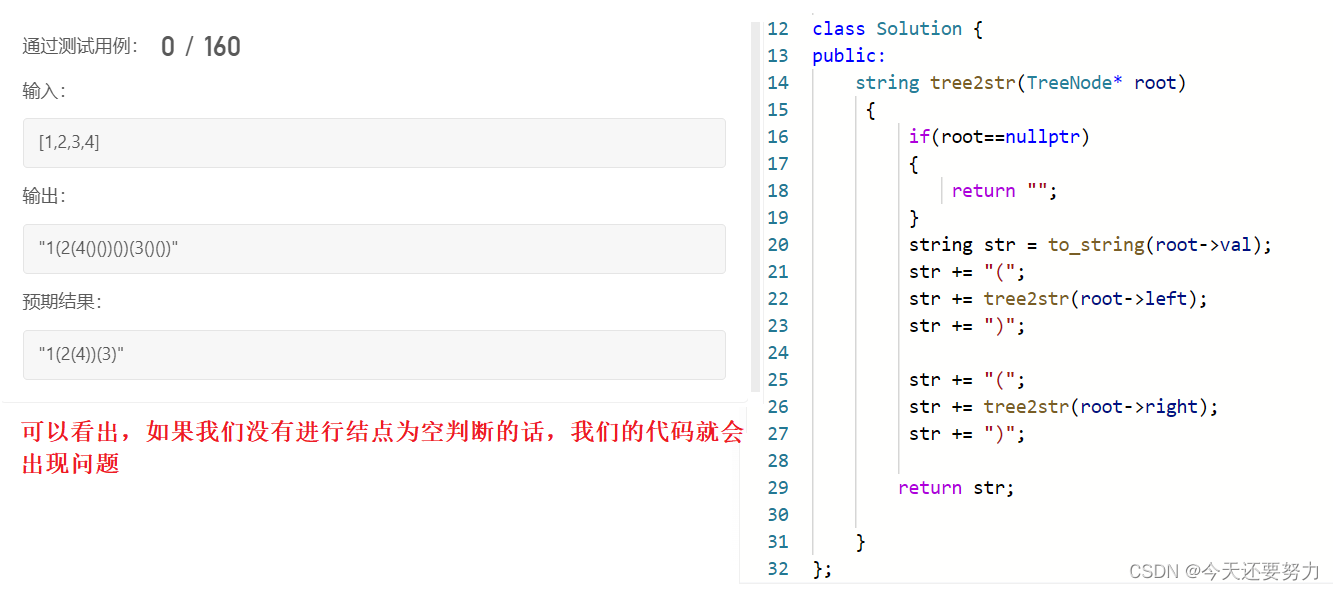
根据我们得出的结论进行改进:
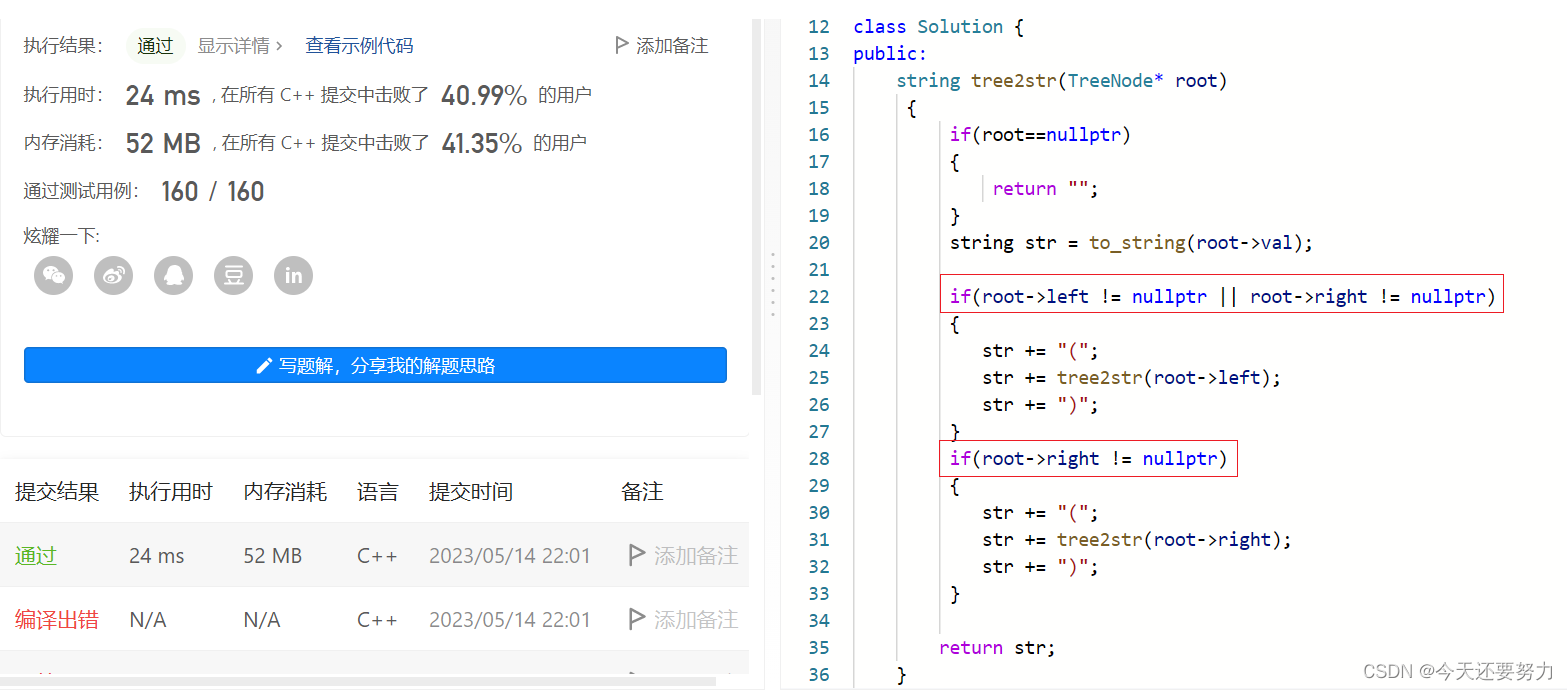
综上所述:就是对上述结论的判断而已,如果不使用按位或,那么你也可以一个场景一个场景的判断,无伤大雅!
第二题:二叉树的层序遍历
详细题目:给你二叉树的根结点root,返回其结点值的层序遍历(即逐层的从左到右访问所有结点)
分析题目:对一棵二叉树进行层序遍历,并且返回该二叉树每一层的结点数据,此时我们就可以直接通过类模板的知识,直接使用 vector<vector<int>> 来解决存储每一层结点数据的工作,而不是像以前使用C语言写代码,需要通过指针数组来返回对应每层的数据
示例一:
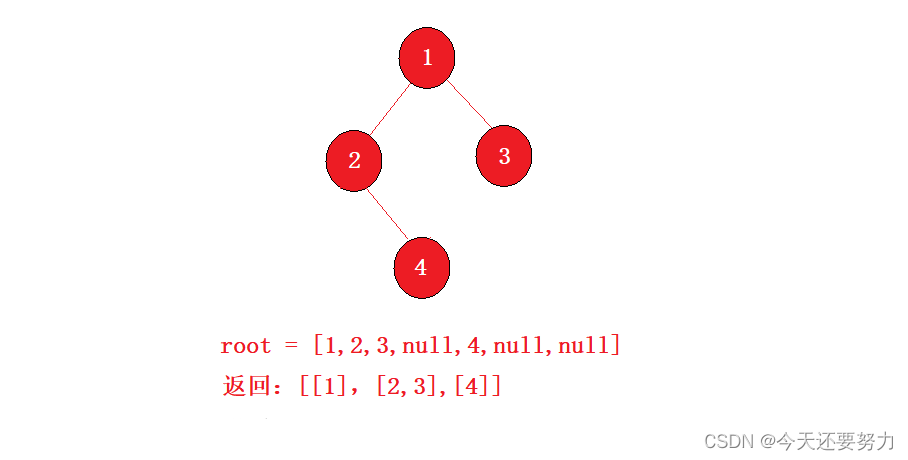
解题思路1:用两个队列(先进先出的特点),queue<Node*>用于记录该层的所有结点,queue< int>用于记录结点层数的个数
解题思路2:用一个队列完成,但是依然需要用一个变量去记录层数,queue<Node*>用于记录该层的所有结点,levelSize用于记录所处层数具有的结点个数
思路二具体原理:因为此时的二叉树时没有任何规律,每一层具体有几个结点我们是不知道的,所以此时就可以通过将每一层结点的左右结点入到队列中,然后再通过计算该队列的大小来确定该层具有的结点个数
所以此时的queue.size()就是我们的levelSize,此时就可以通过queue.size()间接的获取到levelSize,也就是二叉树每一层的数据个数
levelSize具体使用方法如下:
当根入到队列中,此时levelSize就置成1,当根出队列时,levelSize就减减(减到0也就表示出完了),并且根在出的过程中同时也要入左右结点(目的:实现当前层出完队列,下一层的数据全部入到队列),实现当前层出完队列,下一层的数据全部入到队列(先进先出原理),也就是通过levelSize来控制,当levelSize为0,表示的就是当前层出完,下一层全部入完,然后此时只需要通过queue.size()来更新levelSize,此时就获取到了该层的结点个数和出队列的次数
代码如下:(思路二实现)

第三题:自底向上实现层序遍历
明白了上题,此时我们明白,上题使用是从上往下把数据入到对应的队列之中,然后再入到对应的数组中,最后将数组插入到 vector<vector<int>> 中,最后返回题目要求的二叉树的每一层结点数据,同理,该题只不过要求我们把一棵二叉树中的数据按照从下往上的顺序一层一层的遍历,然后放到对应的数组中,最后将该数组再按照下标插入到 vector<vector<int> 中,所以此时我们只要讲该数组给逆序一下,此时返回数组中的数据就是从底层到上层的数据,所以代码如下:
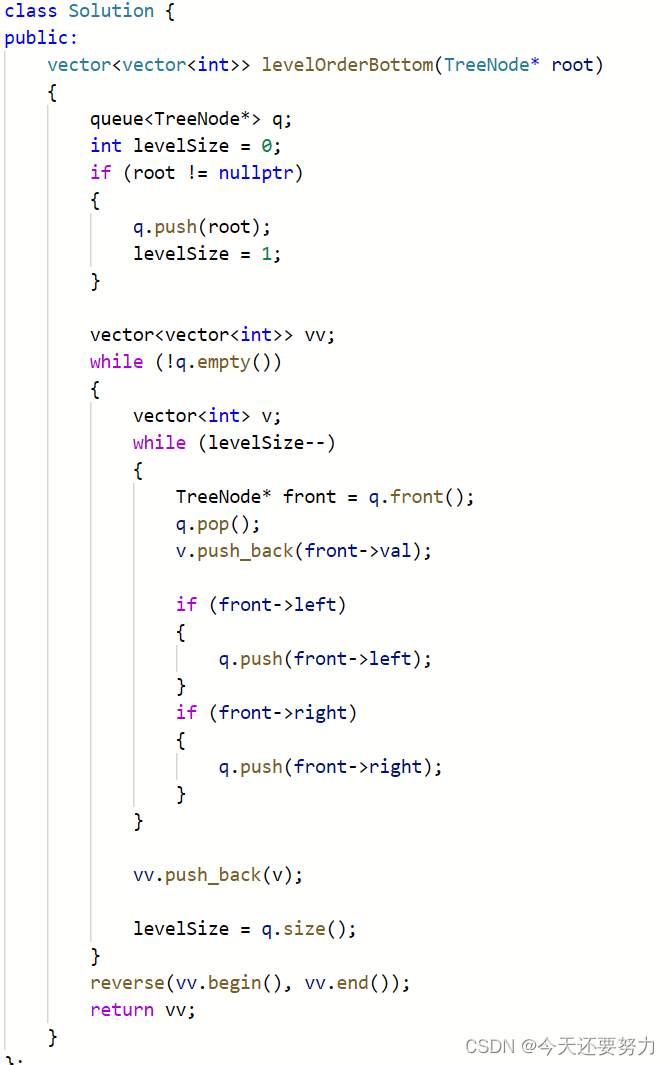
第四题:二叉树的最近公共祖先
详细题目:给定一个二叉树,找到该树中两个指定结点的最近公共祖先,注意:结点自己可以是自己的祖先
图示:
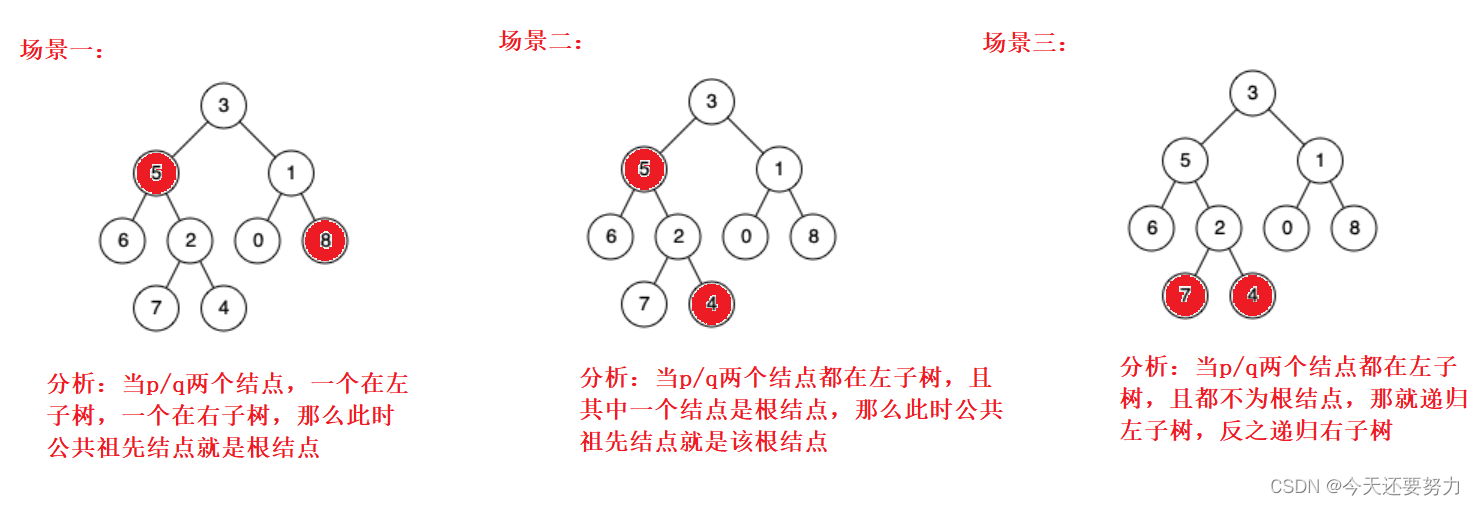
从如上分析可以看出,该题如果想要简单实现是非常容易的,只需要把对应上述的场景给控制住就行了,但是如果你复杂看,也就是考虑到效率问题,那么此时该题就比较的复杂了
首先不考虑效率问题,代码实现如下:
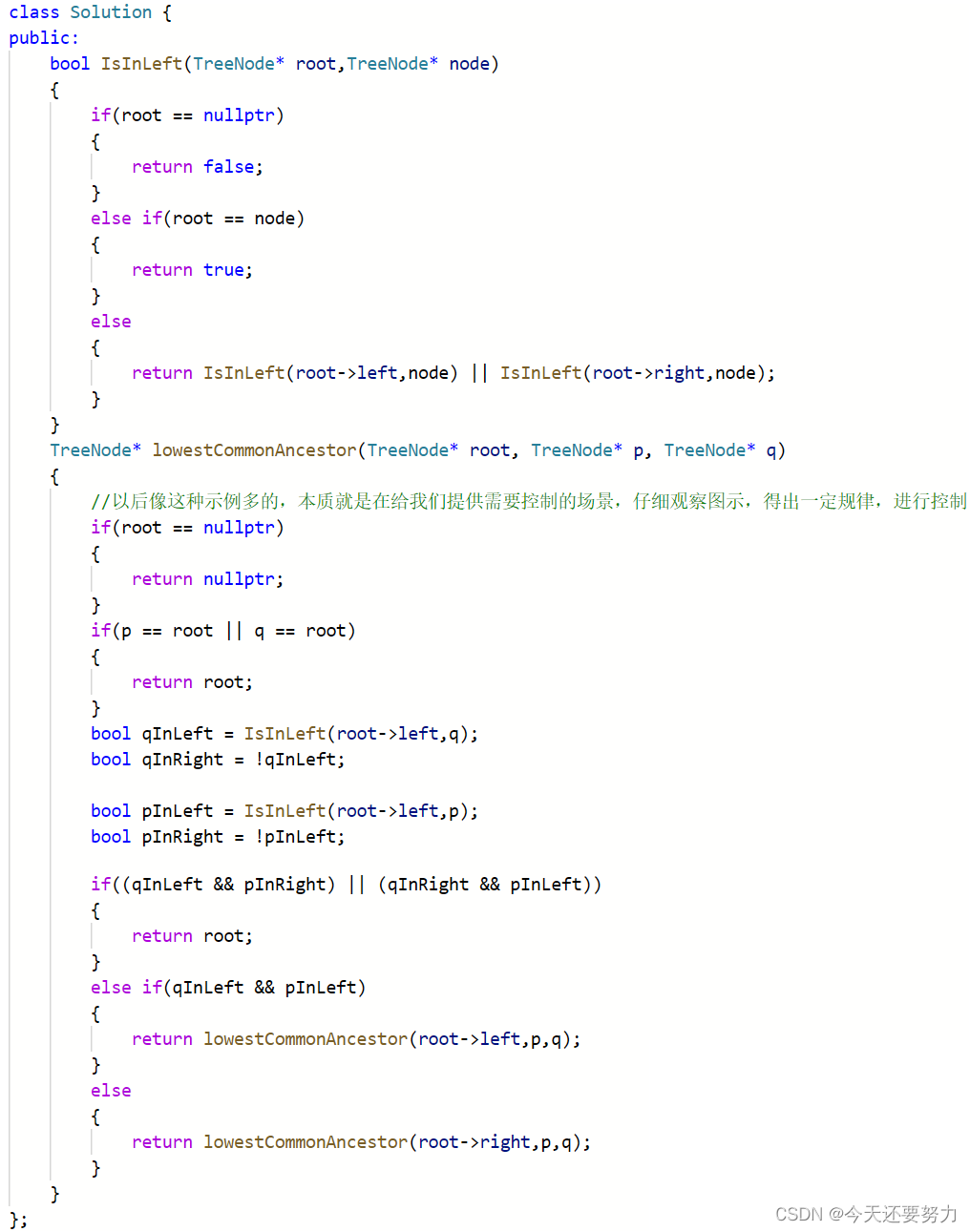
如果想要考虑效率问题,那么我们就需要进行一定的优化,优化思路:
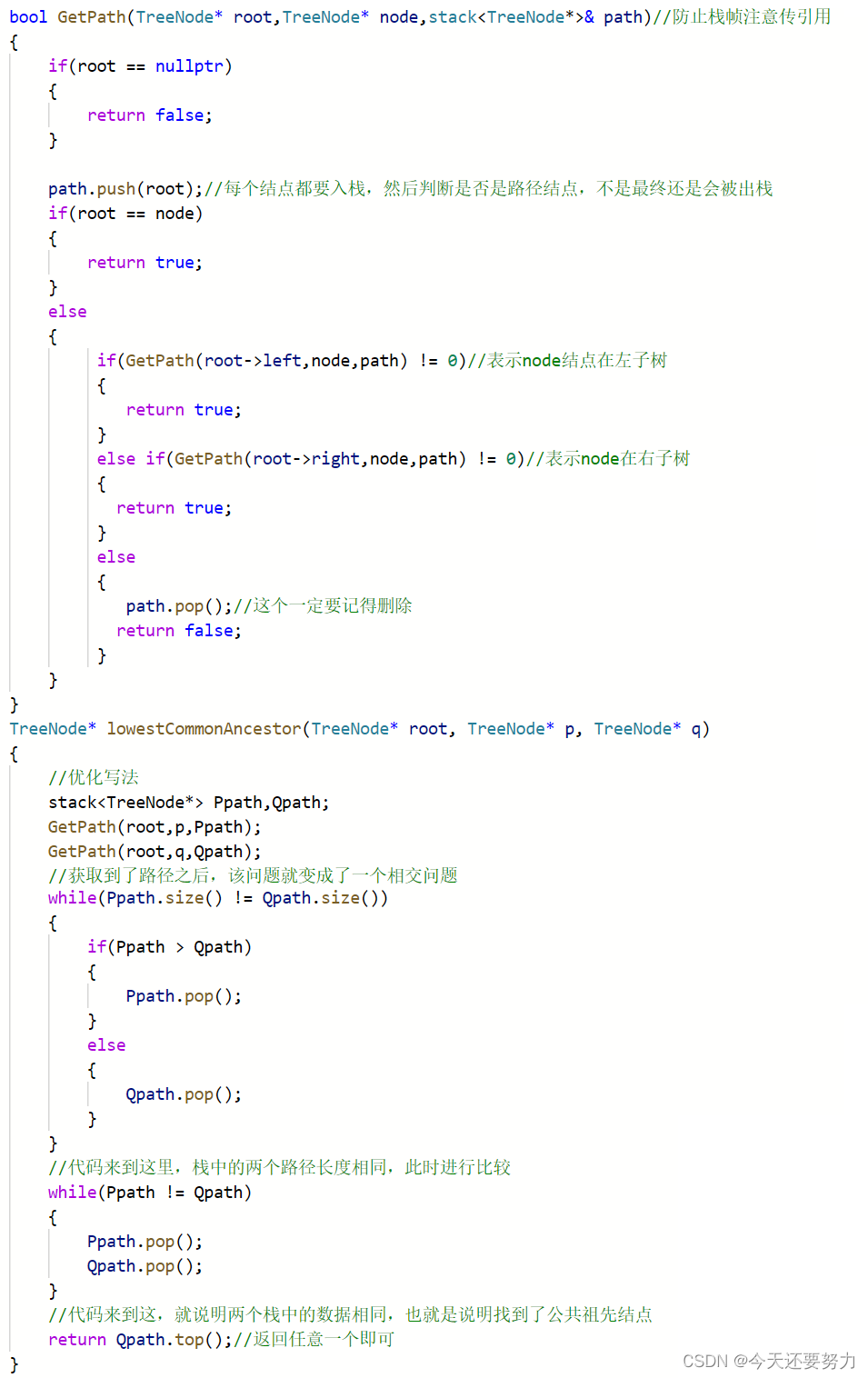
根据DFS(深度优先遍历),求出p和q的路径(使用栈),并且将对应的路径放到对应的容器中,转换成路径相交问题,并且明白前序就是一个深度优先遍历(明白,寻找路径的时候就是一个深度优先遍历而已,类似于迷宫找通路问题)
代码如下:
第五题:将搜索二叉树转换成双向链表
详细题目:输入一棵搜索二叉树,将该二叉树转换成一个排序的双向链表,要求:不能创建任何新的结点,只能调整树中结点指针的指向。当转化完成以后,树中节点的左指针需要指向前驱,树中节点的右指针需要指向后继
图示:
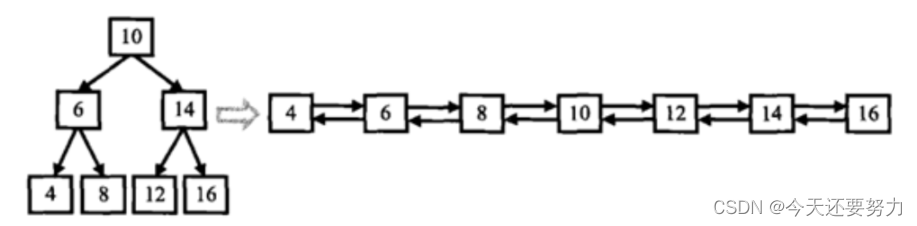
思路:同理中序遍历这棵树(因为是搜索二叉树),同时记录下每一个结点的前驱结点(prev),prev=cur,然后cur再迭代向后走,向后走的同时,只需要让cur的左指针指向prev,此时我们就实现了让每一个结点的左指针指向前驱的效果(具体该结点如何走我们不关心,因为树本身就是一个搜索树,只要中序遍历就行)
但是,还没有中序遍历完成,所以我们并不知道后继在哪里?
解决方法:不能确定cur的下一个是谁(在此代码的该次递归),但是我们一定能知道prev的下一个一定是cur,所以此时我们就可以根本不关心谁是后继,我们只需要让cur跟着中序遍历一步一步的去走就行了,然后通过cur和prev将两个结点给链接起来,关键代码:cur->_left = prev; prev->_right = cur; 这样就可以很好的实现链接(注意:cur会随着中序遍历向后走),所以本质上我们并没有去找后继,因为cur就是prev的后继,而prev=cur;此时就可以实现迭代走走的同时,链接搜索树的每一个结点
代码如下:

第六题:从前序和中序遍历序列构造二叉树
详细题目:给定两个整数数组preorder和inorder,其中preorder是二叉树的前序遍历,inorder是同一棵树的中序遍历,请构造出对应的二叉树并返回其根结点
示例:preorder[] = {3,9,20,15,7}; 根、左、右 inorder = {9,3,15,20,7}; 左、根、右
原理:用前序寻找根结点,再通过中序找左右子树的数据,再去左右子树根据前序找根结点(一定要根据前序找根)
代码如下:

延伸拓展,如何通过中序和后序搞定这个题目,同理,用后序确定根结点位置(根结点此时就是数组中的最后一个数据),然后先创建右子树,再创建左子树,具体为什么先创建右子树,然后左子树,同理前序,当我们获取到了根结点,因为前序是根、左、右,所以按照前序的遍历顺序,此时就应该先构建左子树,再构建右子树,因为在前序的数组中,结点数据是按照前序顺序存储的,根结点后面的那个数据就是左结点(通过preorder就可以理解),此时前序走走是需要按照数组中的顺序的,根完就是左,所以只有这样才刚好可以通过preorder++访问到左,然后让这个左孩子结点成为新的根结点去进行下一次递归(所以一定要先构建左子树),当然如果你不服,你也可以先构建右子树,但是此时你就不能直接通过让数组加加先后走(preorder++),因为这样只能找左,此时你就需要遍历数组,然后通过前序下标对应的数据去中序数组中找到对应的右子树结点对应的下标,显然,这样是更加麻烦的,所以最好的方法就是按照数组中前序的顺序,先找左子树,再找右子树,所以当你需要使用中序和后序构建一棵二叉树时,同理,根据后序找根,左子树、右子树、根,所以此时你想要将左子树和右子树链接到根结点上时,你就需要逆序数组找根,然后同理按照顺序,preorder++,获取到右子树对应的下标,然后去递归右子树
所以综上:这就是为什么使用后序和中序时,要先创建右子树的原因,当然如果你想要先创建左子树也是有办法的,就是要先获取到左子树对应的根结点就行(下标)
第七题:二叉树的前序遍历(非递归)
详细题目:给你二叉树的root结点,返回它结点值的前序遍历
图示:
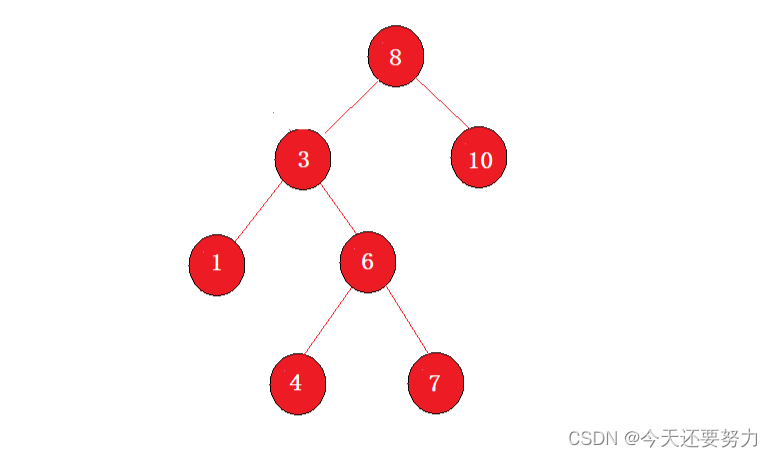
按照迭代原理,此时就是将一棵树分为左路结点和左路结点的右子树(这种方法可以让我们快速掌握前序中序后序的非递归),虽然有别的方式,例如,使用栈,如上图所示也就是:将 8、3、1结点看成左路结点,10、6、4、7看成是左路结点的右子树(右子树中的结点同理看成是左路结点和右子树),然后迭代走走,具体走法:将所有的左路结点入栈(目的:可以更好的去访问左路结点的右子树),将所有左路结点入完之后,开始出栈,此时根据先进后出原理,先出1,但是1的右子树为空,所以返回,此时来到3,出3,然后开始访问3的右子树,同理,将该右子树的所有左路结点入栈(这步只需要循环迭代就可以完成,但注意:此时这样走一次就是一次循环),此时也就是将6、4入栈(栈:8 6 4),然后出栈顶4(top,pop),发现右子树为空,返回,然后6,同理将右子树的左路结点入栈,此时就是将7入栈(栈:8 7),出7,发现右子树为空,返回,栈:8,最终出8,入8右子树的所有左路结点,栈:10,然后发现10的右子树为空,返回,最终整棵树遍历完成
代码如下:

第八题:二叉树的中序遍历(非递归)
思路同理,代码如下:

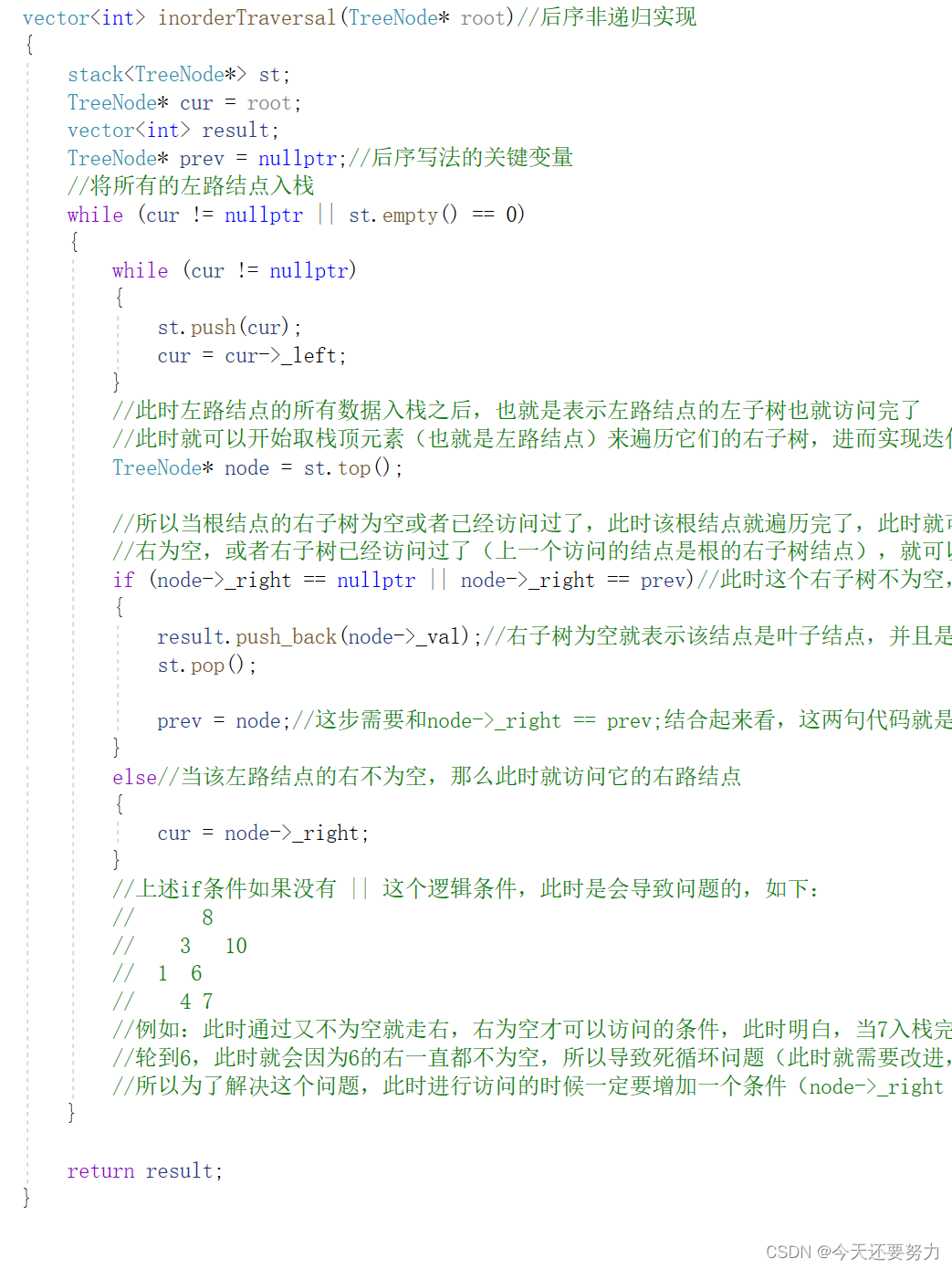
第九题:二叉树的后序遍历(非递归)
思路同理吗,代码如下: