【遇到dfs问题，点进来看看思路】【dfs本质之一全排列思想解决大部分dfs】例题1.全排列例题2.单词接龙

news2024/11/25 10:20:51

在这里插入图片描述

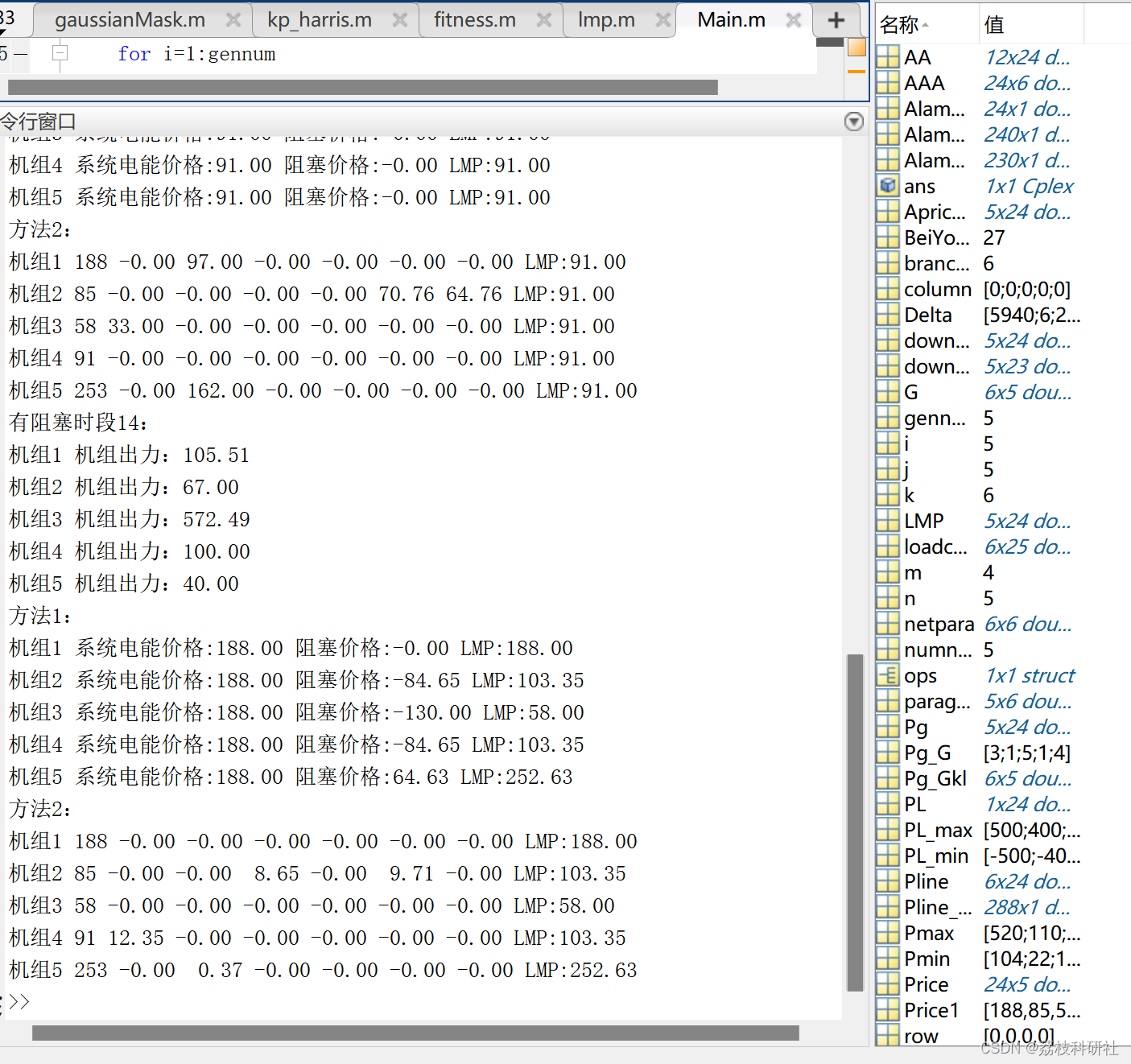
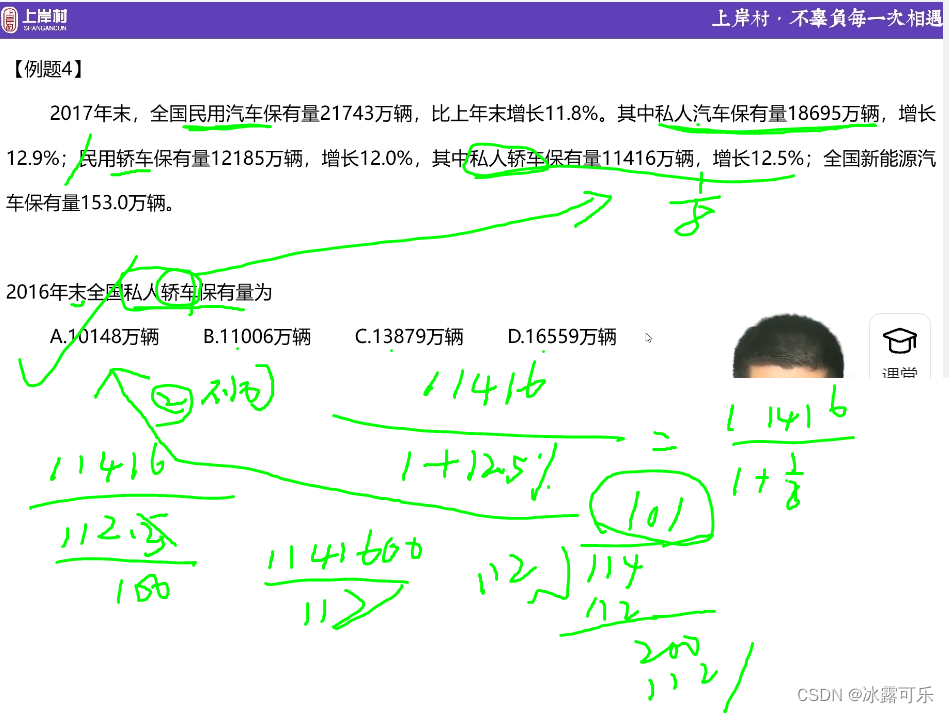
总之就是
在已知格线上，填充可用数据，
如果回退到A，那么把A之前所用数据，换一个，并且A之后的数据都重新填写
这就是全排列（截取的最关键部分，往下看）

这样的话，就是dfs的本质，
当一个方案不行，是中间的哪一步不行，那么我们改变这一步，继续dfs即可（截取的最关键部分，往下看）

欢迎观看我的博客，如有问题交流，欢迎评论区留言，一定尽快回复！（大家可以去看我的专栏，是所有文章的目录）
　
文章字体风格：
红色文字表示：重难点★✔
蓝色文字表示：思路以及想法★✔
　
如果大家觉得有帮助的话，感谢大家帮忙
点赞！收藏！转发！

dfs深搜讲解本质

- 1. 单词接龙
- - - 本题还有个关键就是预处理

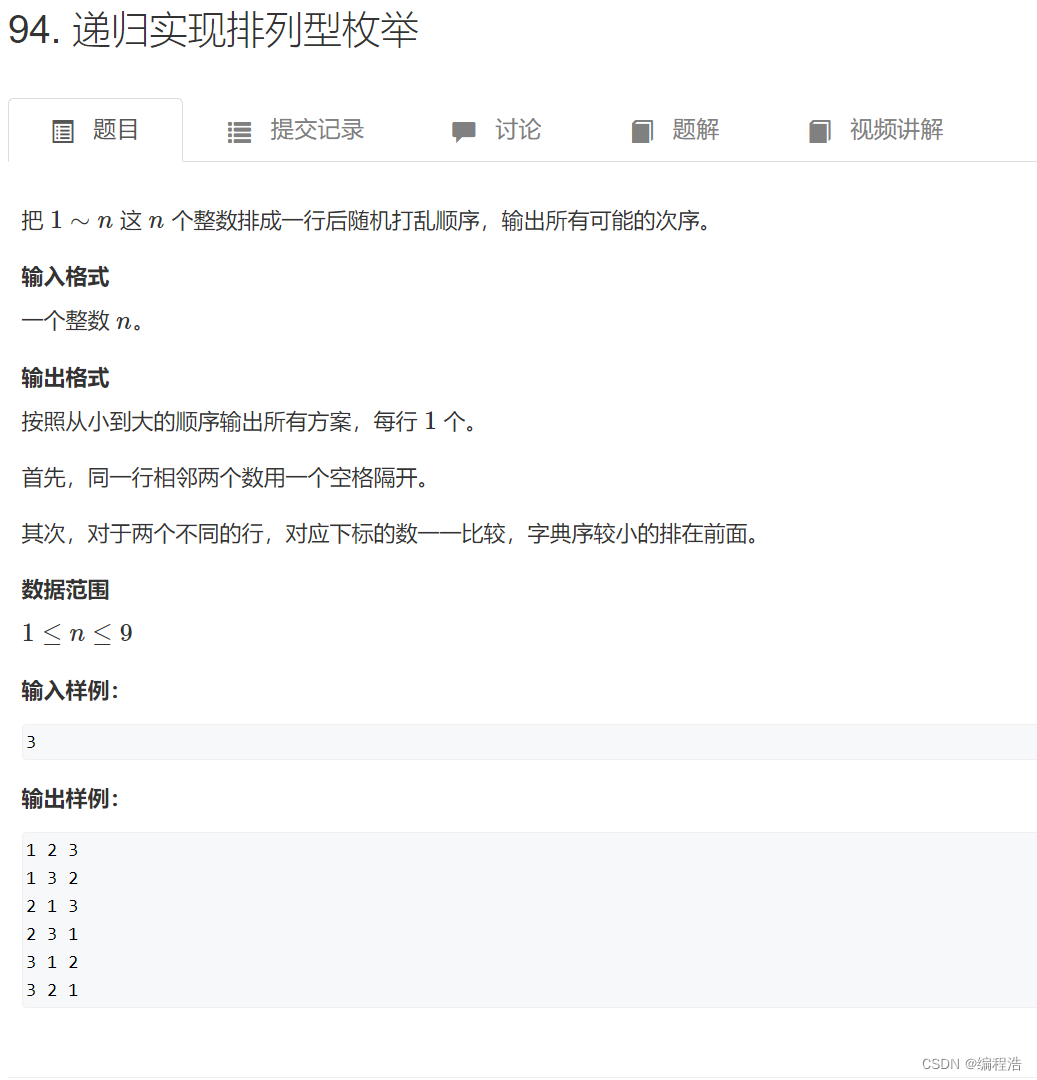
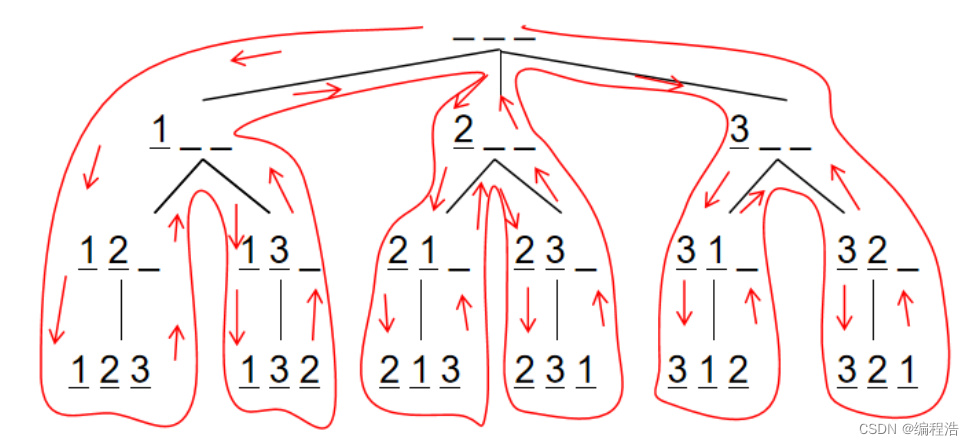
我对于dfs理解源于一道非常经典的例题

就是全排列问题

如下

在这里插入图片描述

#include<iostream>
using namespace std;
const int N = 10;
int path[N];//保存序列
int state[N];//数字是否被用过
int n;
void dfs(int u)
{
    if(u > n)//数字填完了，输出
    {
        for(int i = 1; i <= n; i++)//输出方案
            cout << path[i] << " ";
        cout << endl;
    }

    for(int i = 1; i <= n; i++)//空位上可以选择的数字为:1 ~ n
    {
        if(!state[i])//如果数字 i 没有被用过
        {
            path[u] = i;//放入空位
            state[i] = 1;//数字被用，修改状态
            dfs(u + 1);//填下一个位
            state[i] = 0;//回溯，取出 i
        }
    }
}

int main()
{

    cin >> n;
    dfs(1);
    return 0;
}

这道经典题，就不解析了。大家可以看代码理解一下

主要是上面的图，有助于我们解决dfs问题

上述的图是一个树，表示出来dfs的本质

也就是 dfs最开始是知道需要填充多少个格线的
（如果不知道也可以）

总之就是
在已知格线上，填充可用数据，
如果回退到A，那么把A之前所用数据，换一个，并且A之后的数据都重新填写
这就是全排列

1. 单词接龙

在这里插入图片描述

#include <cstring>
#include <iostream>
#include <algorithm>

using namespace std;

const int N = 21;

int n;
string word[N];
int g[N][N];//代表编号i的可以被j拼接  如i：asd，j：sdf，拼接长度为最小值g[i][j] = 2，i从0开始记位
int used[N];//编号为i的单词使用次数
int ans;

void dfs(string dragon, int last) 
{
    ans = max((int) dragon.size(), ans);//取最大值，dragon.size()为当前合并的长度

    used[last]++;//编号为last的单词被用次数++；

    for (int i = 0; i < n; i++)
        if (g[last][i] && used[i] < 2)//used[i]<2代表单词用次数不超过2
            dfs(dragon + word[i].substr(g[last][i]), i); //编号为last的可以被i拼接现在尾巴为i号

    used[last]--;//恢复现场
}

int main() {
    cin >> n;
    for (int i = 0; i < n; i++) cin >> word[i];
    char start;
    cin >> start;//首字母

    for (int i = 0; i < n; i++)//遍历得到各个g[i][j]
        for (int j = 0; j < n; j++) {
            string a = word[i], b = word[j];
            for (int k = 1; k < min(a.size(), b.size()); k++)
                if (a.substr(a.size() - k, k) == b.substr(0, k)) {
                    g[i][j] = k;
                    break;
                }
        }

    for (int i = 0; i < n; i++)//找到首字母为strat的单词开始做dfs，dfs中会自动找到最大值
        if (word[i][0] == start)
            dfs(word[i], i);//从word[i]开始遍历，i代表现在是第几个单词

    cout << ans << endl;

    return 0;
}

本题还有个关键就是预处理

在这里插入图片描述

预处理这个思想很重要，

这道题是怎么预处理的呢？

由于我们需要知道，所有单词之间，两两关系
所以我们预先

for (int i = 0; i < n; i++)//遍历得到各个g[i][j]
    for (int j = 0; j < n; j++) {
        string a = word[i], b = word[j];
        for (int k = 1; k < min(a.size(), b.size()); k++)
            if (a.substr(a.size() - k, k) == b.substr(0, k)) {
                g[i][j] = k;
                break;
            }
    }