后续可能会有补充和更改

目录

一、数据结构 

1.算法介绍

二、时间复杂度、空间复杂度

三、练习

1.时间复杂度

2.空间复杂度 

---

一、数据结构 

数据结构是计算机存储、组织数据的方式，指相互之间存在一种或多种特定关系的数据元素的集合。

数据结构和数据库的区别

数据结构是在内存中存储管理数据的，数据库是在磁盘中存储管理数据的。

二者的本质都是存储管理数据。

内存和磁盘的区别

内存：带电存储（如果电脑突然关机，没有保存，则数据丢失。要快速访问，用内存，用数据结构）

磁盘：不带电存储（存储到数据库中、或以文件形式存储，项目当中存储的数据方便查找数据，方便遍历数据，最好用数据库存储。想持久化，长期保存下来，用数据库） 

算法就是对数据按要求进行某些处理，将输入数据转换成想要的输出结果。例如：查找、排序...... 

二、时间复杂度、空间复杂度

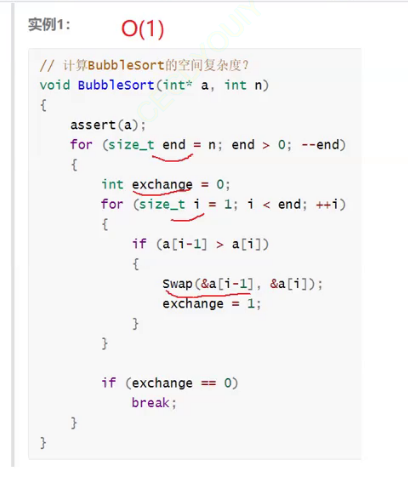
时间复杂度主要衡量一个算法的运行快慢，而空间复杂度主要衡量一个算法运行所需要的额外空间。（注意，空间复杂度不是计算程序占用了多少字节的空间，而是计算的是变量的个数。即时间复杂度算次数，空间复杂度算额外变量个数）

衡量一个算法的好坏，主要看其时间复杂度和空间复杂度，它们也是衡量性能、效率的两个主要指标。复杂度是用来计算算法中基本操作的执行次数的。实际中一般取的是算法的最差运行情况。

算复杂度不要数循环，因为它不一定准确，而是要看算法思想。

冒泡排序的时间复杂度：

二分查找的时间复杂度：O(logN)以二为底。最好情况为O(1)

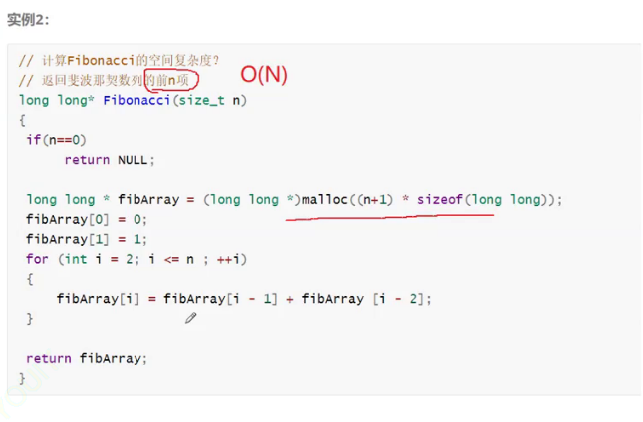
空间复杂度

斐波那契数列的空间复杂度：O(N)

注意：时间是累积的，空间是不累积的，可以重复利用

 第二节1:03:00

复杂度一般用大O的渐进表示法来表示

推导大O的方法：

1.用常数1取代运行时间中的所有加法常数（无论是多大的常数，因为现在计算机计算速度特别快，平时用到的常数次并不算多）

2.在修改后的运行次数函数中，保留最高阶项

算法中的基本操作的执行次数，为算法的时间复杂度。

3.如果最高阶项存在且不是1，则去除与这个项目相乘的常数。得到的结果就是大O阶。

如果遇到O(N+M)，N和M都是常数，这时，如果N远大于M，则是O(N)，M远大于N，则是O(M)，M和N一样大，就是O(N)或O(M)

O(1)表示的是常数次

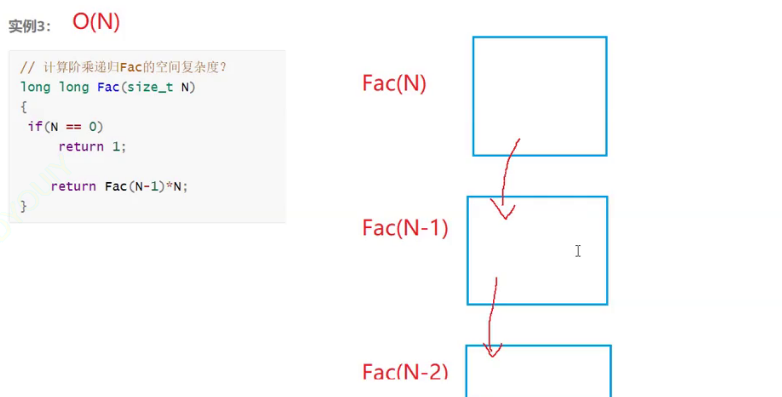
函数（递归......）的时间复杂度：函数的深度及各层深度计算次数相加

很多算法大部分情况下，空间复杂的都是O(1),不是O(1)就是O(n)。

注意：函数运行时所需要的栈空间（存储参数、局部变量、一些寄存器信息等）在编译期间已经确定好了，因此空间复杂度主要通过函数在运行时显式申请的额外空间来决定

一般logn都是以2为底

栈的大小一般只有8MB

递归的深度太深时，空间不够 ，栈会溢出，栈溢出就是空间不够

三、练习

1.时间复杂度

1.下列有关大O表示法的说法错误的是（）

A.大O表示法只是对程序执行的一个估算

B.大O表示法只保留最高阶项

C.大O表示法会保留一个系数来更准确的表示复杂度

D.大O表示法一般表示的是算法最差的运行时间

选C

大O是一个渐进表示法，不会去表示精确的次数，cpu的运算速度很快，估计精确的没有意义。

B：随着问题规模的增加，次高阶项和更低阶项对总时间的影响逐渐减小，最终可以忽略不计

C：大O表示法通常不会保留一个系数来更准确地表示复杂度，因为在算法分析中，常数项通常不是很重要，会随着具体实现方式和硬件环境的不同而变化。

2.分析以下函数的时间复杂度

void fun(int n) {
  int i=l;
  while(i<=n)
    i=i*2;
}

O(logN)

该循环并没有被执行n次，i每次都是变为自己的2倍，所以循环只会被执行log以2为底的n次

3. 分析以下程序的时间复杂度

for(int i=0;i<n;i++)
  for(int j=0;j<n;j++)
    a[i][j]=i*j;

O(N^2)

程序有两次循环，每个循环都有n次操作，所以时间复杂度为n^2

4.下面算法的时间复杂度是

  int f ( unsigned int n ) {
    if (n == 0 || n==1) 
      return 1;
    else 
      return n * f(n-1);
  }

O(N)

此函数会被递归调用n - 1次，每次操作都是一次，所以时间复杂度为n

5.给定一个整数sum，从有N个有序元素的数组中寻找元素a，b，使得a+b的结果最接近sum，最快的平均时间复杂度是

O(N)

可以使用双指针法来解决这个问题，最快的平均时间复杂度是 O(N)

具体实现步骤如下：

1.将指针 left 指向数组的第一个元素，将指针 right 指向数组的最后一个元素。

2.计算 left 和 right 指向的元素之和。

3.如果和大于sum，则将 right 指针向左移动一位，以减小和。

如果小于sum，则将 left 指针向右移动一位，以增大和。

如果等于sum，则直接返回a和b。

在移动指针的过程中，还需记录最接近目标值的a和b，以及对应的 arr[left]和arr[right] 值。当left和right指针相遇时，结束。

因为该算法只需要遍历一次数组，每次操作都只涉及到两个指针的移动和数值的比较，因此时间复杂度是 O(N)。

6.设某算法的递推公式是T(n)=T(n-1)+n，T(0)=1，则求该算法中第n项的时间复杂度为

O(N)

T(n)

=T(n-1)+n

=T(n-2)+(n-1)+n

=T(n-3)+(n-2)+(n-1)+n

...

=T(0)+1+2+...+(n-2)+(n-1)+n

=1+1+2+...+(n-2)+(n-1)+n

该题即将T(n)推演到T(0)，共递归了n次，相加次数为1+1到n，为n+1次，所以时间复杂度为O(N)

2.空间复杂度 

1.如果一个函数的内部中只定义了一个二维数组a[3][6]，请问这个函数的空间复杂度为

O(1)

函数内部数组的大小是固定的，空间复杂度计算的是额外空间的大小，所以不论函数运行多少次，所需空间都是固定大小的，因此空间复杂度为O(1)

2.分析以下函数的空间复杂度

  int** fun(int n) {
    int ** s = (int **)malloc(n * sizeof(int *));
    while(n--)
      s[n] = (int *)malloc(n * sizeof(int));
    return s;
  }

O(N^2)

先是为二级指针开辟空间，大小为n个一级指针。

然后分别为二级指针的每个指针开辟空间。

实际开辟后的是一个二维数组，数组有n行，每行分别有1,2,3,...n列，所以是n(n + 1)/2个元素空间。空间复杂度为O(N^2)