∗ ∗ 重点:状态值、贝尔曼方程 ∗ ∗ **重点:状态值、贝尔曼方程** ∗∗重点:状态值、贝尔曼方程∗∗
return评估策略
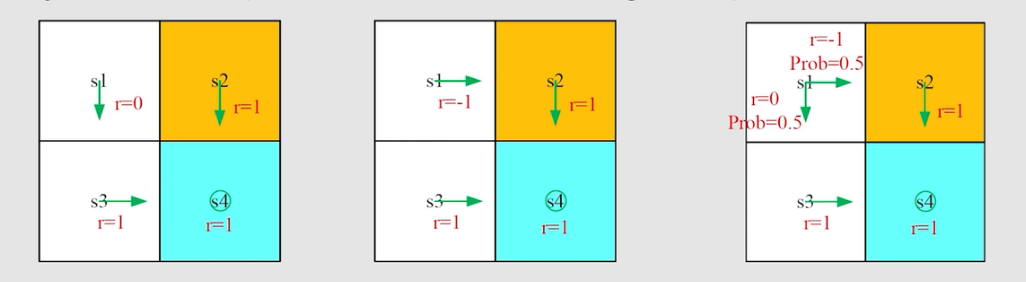
在前面概念介绍中,我们知道了可以用 return 来评估一个策略的好坏。如图,有三个不同的策略,那么哪一种策略最好呢?这时,就需要借助 return 来进行评估了。
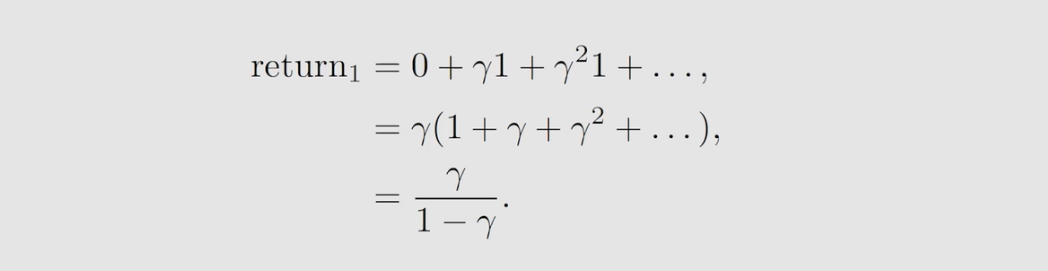
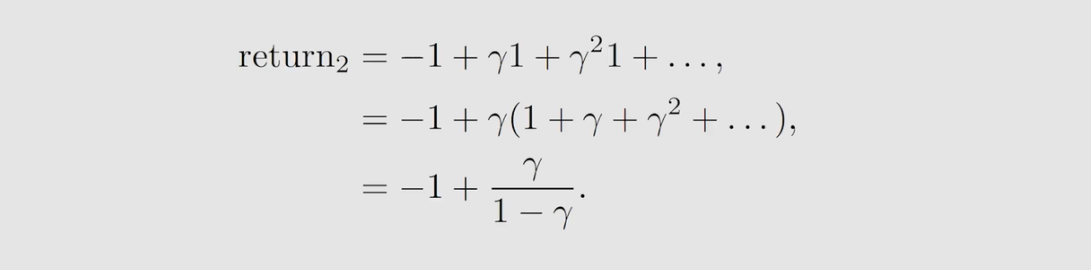
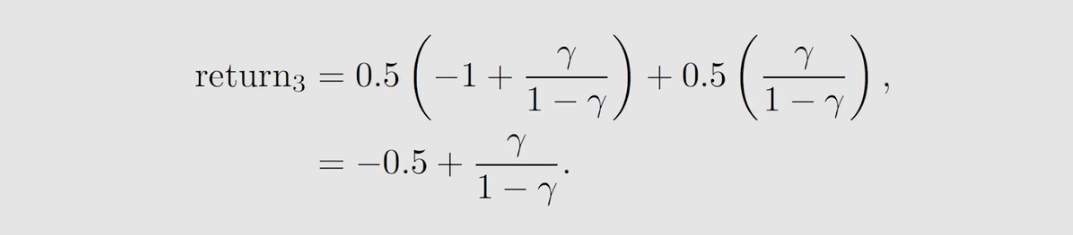
return的计算
既然 return 这么重要,那么怎么计算呢?上述例子 return 的计算是用的return 的定义,实际上还有更好的计算方法。

如何计算上图的return?为了方便计算,我们引入
v
i
v_i
vi ,用来记录从状态
s
1
s_1
s1 出发得到的 return。
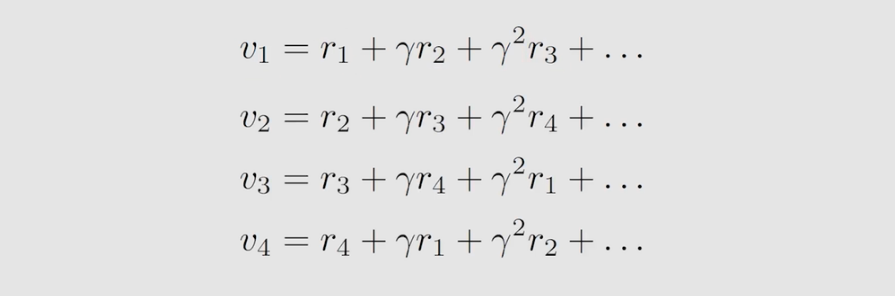
将上述式子变形,得到下列式子:
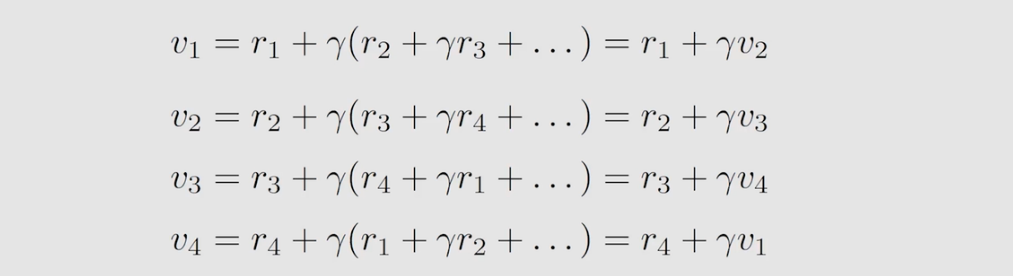
上面式子表明从不同状态出发得到的 return 依赖于从其他状态出发得到的 return 。可以发现,上面式子有这样一个特征,可以通过自身不断迭代得到自身,如下图,该方法被称为 Bootstrapping 。

为什么可以通过自身不断迭代得到自身?我们可以用数学来描述就知道其中的原因了。首先,将上面式子写成矩阵形式,如下图。根据线性代数知识可以得到最终
v
v
v。
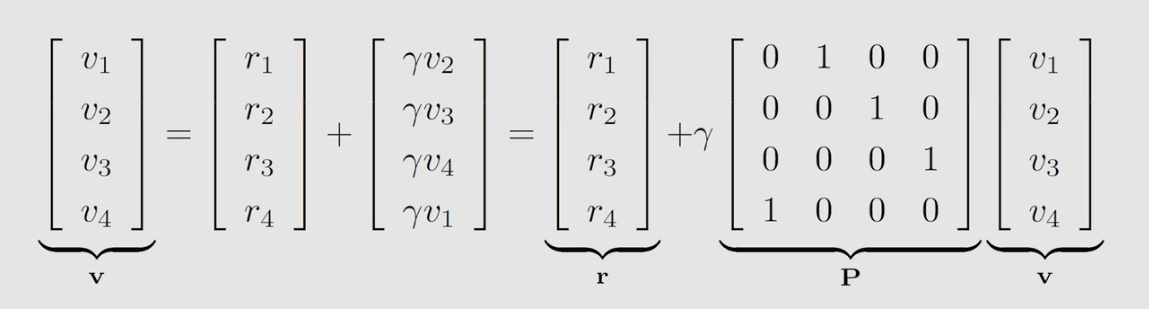
v
=
r
+
γ
p
v
v=r+γpv
v=r+γpv
v
=
(
E
−
γ
p
)
r
v=(E-γp)r
v=(E−γp)r
上面式子 v = r + γ p v v=r+γpv v=r+γpv 即就是贝尔曼方程(对于这个特定的确定性问题)。虽然很简单,但它展示了核心思想:一个状态的value 依赖于其他状态的 value。
状态值 state value
为了更好的理解 state value ,我们首先以一个单步过程为例引入一些符号。
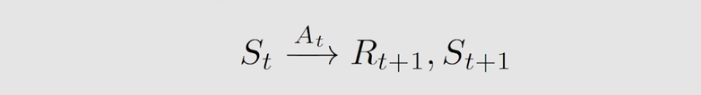
S
t
S_t
St:
t
t
t 时刻的状态
A
t
A_t
At:
S
t
S_t
St 状态下采取的行为
R
t
+
1
R_{t+1}
Rt+1:在
S
t
S_t
St 状态下采取
A
t
A_t
At 行为后获得的奖励
S
t
+
1
S_{t+1}
St+1:
S
t
S_t
St 状态下采取行为
A
t
A_t
At后转移到的新状态
上面式子所涉及的所有跳跃,都是基于概率分布来的
S
t
S_t
St→
A
t
A_t
At:依赖于
π
(
A
t
=
a
∣
S
t
=
s
)
π(A_t=a|S_t=s)
π(At=a∣St=s)
S
t
S_t
St→
A
t
A_t
At:依赖于
p
(
R
t
+
1
=
r
∣
S
t
=
s
,
A
t
=
a
)
p(R_{t+1}=r|S_t=s,A_t=a)
p(Rt+1=r∣St=s,At=a)
S
t
S_t
St→
A
t
A_t
At:依赖于
p
(
S
t
+
1
=
s
′
∣
S
t
=
s
,
A
t
=
a
)
p(S_{t+1}=s'|S_t=s,A_t=a)
p(St+1=s′∣St=s,At=a)
注意:其中的
R
t
+
1
R_{t+1}
Rt+1 有时也会写成
R
t
R_t
Rt ,两者从数学上来说没有区别,但我们习惯性写成
R
t
+
1
R_{t+1}
Rt+1
由单步过程可以推广出多步过程,并求得 discount return 我们用
G
t
G_t
Gt 表示。
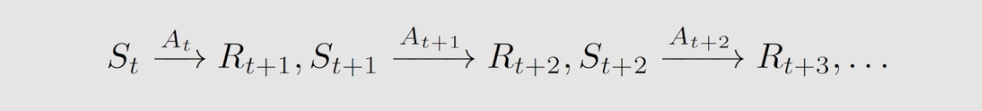
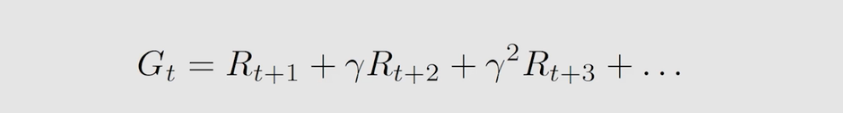
.
有了上面的基础,现在我们可以正式来定义 state value 了,我们将state value 即
v
v
v 定义为
G
t
G_t
Gt 的期望(或称为期望值或均值):
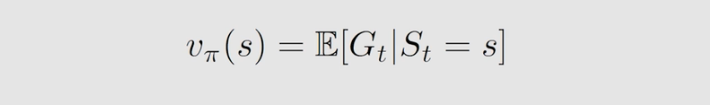
1、
v
π
(
s
)
v_π(s)
vπ(s) 是
S
S
S 的一个函数,是带有条件的条件期望,从不同状态出发得到 trajectory 不同,对应的期望也是不同的
2、
v
π
(
s
)
v_π(s)
vπ(s) 是基于策略
π
π
π 的,对于不同的策略得到的状态值可能是不同。
3、
v
π
(
s
)
v_π(s)
vπ(s) 不仅仅代表一个状态值,也可以代表一种价值,状态值比较大说这个状态是有价值的,因为从这个状态出发回获得更大的 return
return 与 state value 的区别:
return 是针对单个 trajectory 求得的,而 state value 状态值是针对多个 trajectory 求得的 return 再求平均值得到的。如果所有的
π
(
A
t
=
a
∣
S
t
=
s
)
π(A_t=a|S_t=s)
π(At=a∣St=s)、
p
(
R
t
+
1
=
r
∣
S
t
=
s
,
A
t
=
a
)
p(R_{t+1}=r|S_t=s,A_t=a)
p(Rt+1=r∣St=s,At=a)、
p
(
S
t
+
1
=
s
′
∣
S
t
=
s
,
A
t
=
a
)
p(S_{t+1}=s'|S_t=s,A_t=a)
p(St+1=s′∣St=s,At=a)是确定性的,则return 与 state value 相同。
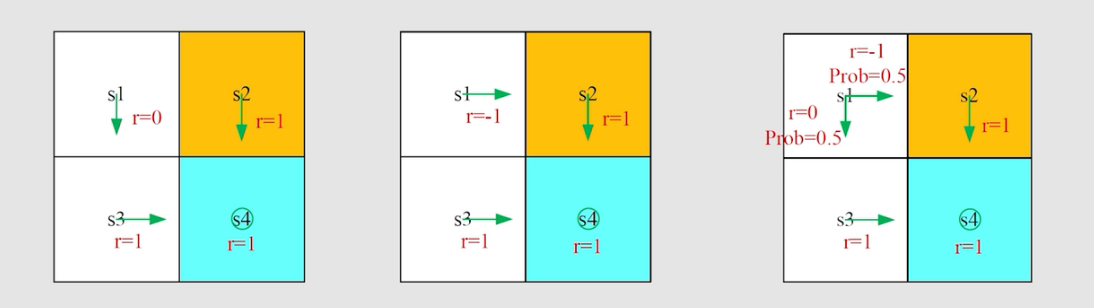
例如,下面的三个策略对应的 trajectory 不同,而
π
1
π_1
π1、
π
2
π_2
π2得到的 return 与 state value 值是相同的;
π
3
π_3
π3对应得到的则是 state value 。
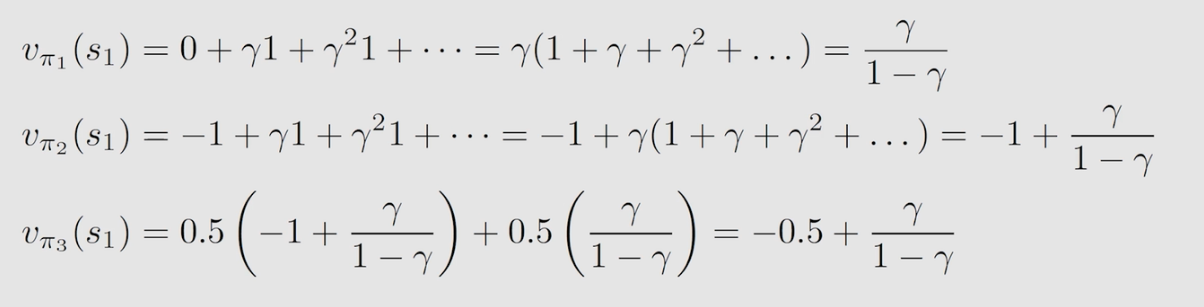
贝尔曼方程:推导
通过上述的介绍,现在我们可以试着推到一般性的贝尔曼方程了。现在,下列的式子相信都可理解。第二个式子表明,t时刻获得的 return 可以表示为立即得到的奖励与从下一时刻出发的到的 return 乘以衰减系数的和。将第二个式子代入 state value 方程得到第三个式子。
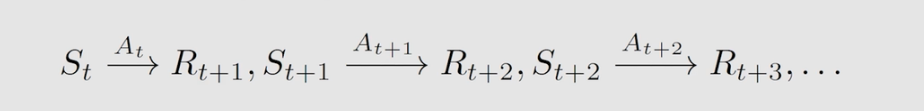
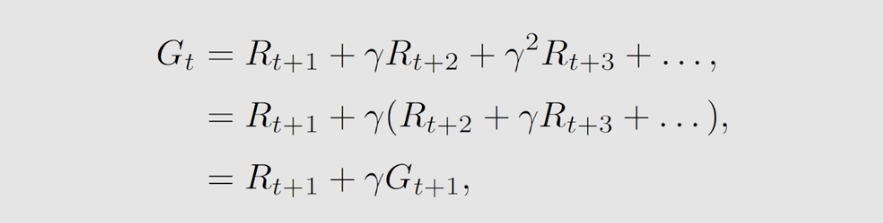

.
现在,分别来看第三式子的两部分:
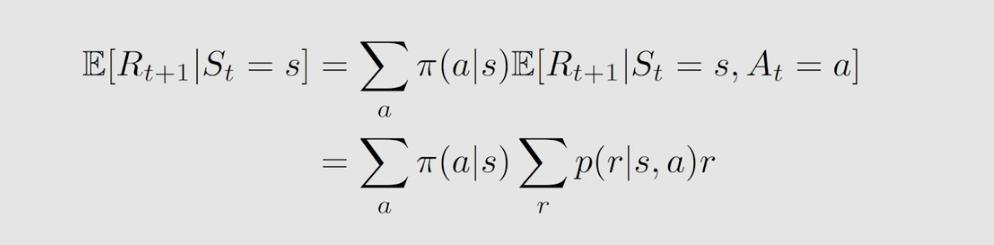
第一项的本质是及时奖励的平均值。首先,在状态
s
s
s 下有多个行为可以选择,采取行为
a
a
a 的概率就是
π
π
π ;而执行行为
a
a
a 所得到的奖励就是期望
E
E
E(从状态
s
s
s 出发采取行为
a
a
a 得到奖励
r
r
r 的概率乘以它本身的值
r
r
r ,即枚举所有动作对应的概率和奖励,将对应的概率乘以奖励求和就得到了期望)
.
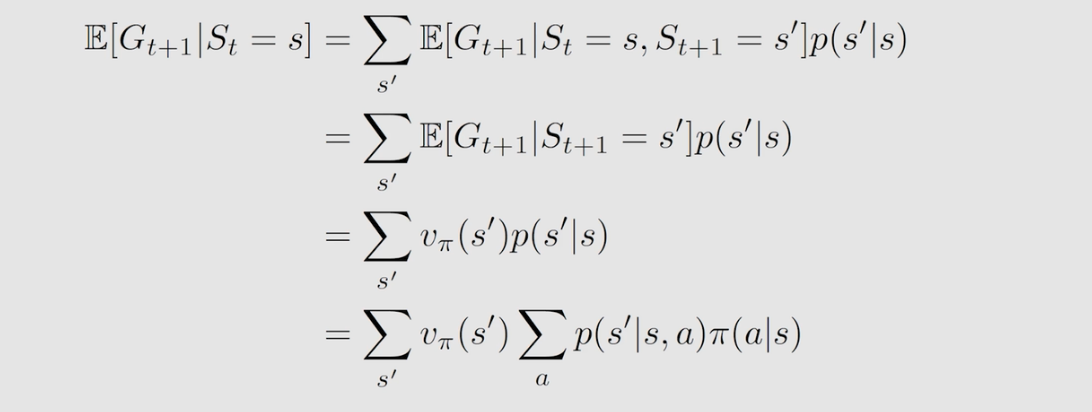
第二项的本质是未来奖励的平均值。从当前状态
s
s
s 出发通过不同的行为
a
a
a 跳到不同的
s
′
s'
s′ 的概率
p
(
s
′
∣
s
)
p(s'|s)
p(s′∣s) ; 与第一项同理得到跳到状态
s
′
s'
s′ 获得的值是期望
E
E
E ,又因为无后效性,所以跳到状态
s
′
s'
s′ 获得的值就等于状态
s
′
s'
s′ 对应的状态值。从状态
s
s
s 到状态
s
′
s'
s′ 的概率等于 从状态
s
s
s 出发通过选择不同的行为
a
a
a 的概率
π
π
π 乘以选择行为
a
a
a 跳转到
s
′
s'
s′ 的的概率
p
(
s
′
∣
s
,
a
)
p(s'|s,a)
p(s′∣s,a),再累计相加。
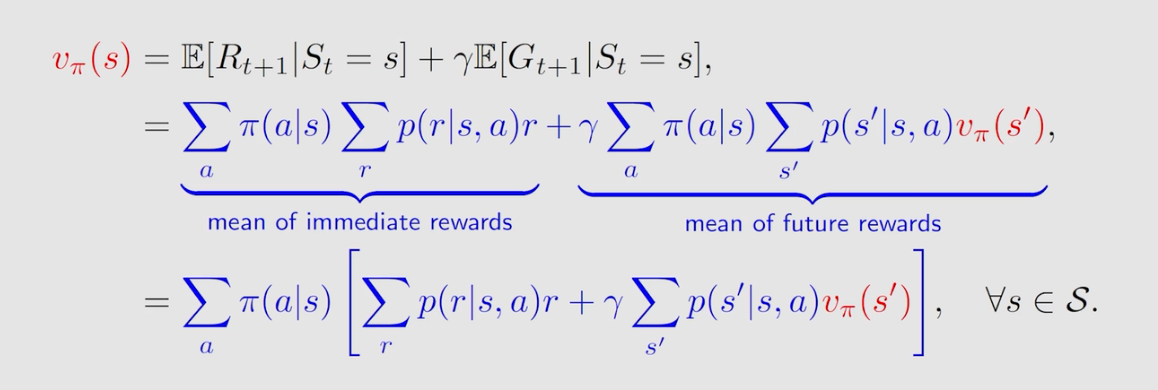
因此,我们得到上面这个式子,即为一般形式的贝尔曼方程。可以看出贝尔曼方程实际上是描述不同状态下的状态值之间的关系;由两项组成:及时奖励的平均值和未来奖励的平均值;另外该式子对状态空间中的所有状态都成立。可以看到
v
π
(
s
)
v_π(s)
vπ(s) 和
v
π
(
s
′
)
v_π(s')
vπ(s′) 都是要计算的状态值,计算方法为 Bootstrapping ,因为实际上是有一组这样的式子,把这些式子联立起来就可以求解了,解的过程依赖与很多概率。
.
为了更好的理解贝尔曼方程,我们以一个例子进行讲解。

首先把这个问题中所有的贝尔曼公式全部写出来,我们首先考虑状态
s
1
s_1
s1 ,根据给出的策略可以把贝尔曼涉及的变量全部确定出。
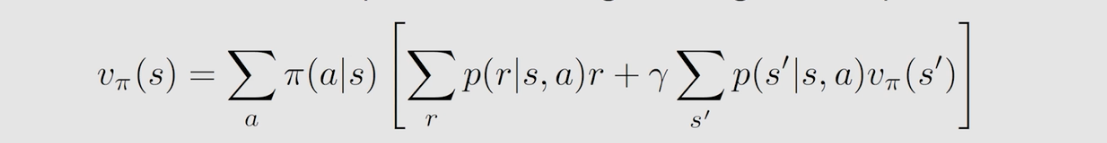
π
(
a
=
a
3
∣
s
1
)
=
1
π
(
a
≠
a
3
∣
s
1
)
=
0
π(a=a_3|s_1)=1 \quad π(a≠a_3|s_1)=0
π(a=a3∣s1)=1π(a=a3∣s1)=0
p
(
s
′
=
s
3
∣
s
1
,
a
3
)
=
1
p
(
s
′
≠
s
3
∣
s
1
,
a
3
)
=
0
p(s'=s_3|s_1,a_3)=1 \quad p(s'≠s_3|s_1,a_3)=0
p(s′=s3∣s1,a3)=1p(s′=s3∣s1,a3)=0
p
(
r
=
0
∣
s
1
,
a
3
)
=
1
p
(
r
≠
0
∣
s
1
,
a
3
)
=
0
p(r=0|s_1,a_3)=1 \quad p(r≠0|s_1,a_3)=0
p(r=0∣s1,a3)=1p(r=0∣s1,a3)=0
我们很容易得到状态
s
1
s_1
s1 的贝尔曼方程,同理得到其他状态的贝尔曼方程,如下:
v
π
(
s
1
)
=
0
+
γ
v
π
(
s
3
)
v_π(s_1)=0+γv_π(s_3)
vπ(s1)=0+γvπ(s3)
v
π
(
s
2
)
=
1
+
γ
v
π
(
s
4
)
v_π(s_2)=1+γv_π(s_4)
vπ(s2)=1+γvπ(s4)
v
π
(
s
3
)
=
1
+
γ
v
π
(
s
4
)
v_π(s_3)=1+γv_π(s_4)
vπ(s3)=1+γvπ(s4)
v
π
(
s
4
)
=
1
+
γ
v
π
(
s
4
)
v_π(s_4)=1+γv_π(s_4)
vπ(s4)=1+γvπ(s4)
得到了所有状态对应的贝尔曼方程,求解结果如下:

如果
γ
=
0.9
γ=0.9
γ=0.9 则有:
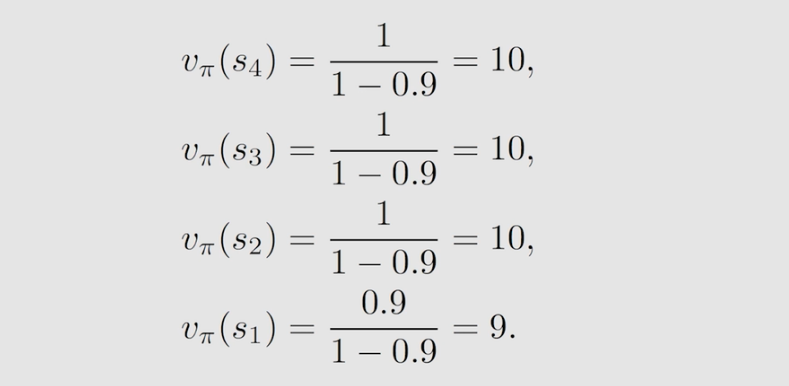
可以看到
v
π
(
s
1
)
v_π(s_1)
vπ(s1)=
v
π
(
s
,
2
)
v_π(s,2)
vπ(s,2) =
v
π
(
s
3
)
v_π(s_3)
vπ(s3)=10,为什么全大于
v
π
(
s
1
)
v_π(s_1)
vπ(s1) 呢?因为状态值代表它的价值,这里显示出来的价值是因为他们离目标近。
.
例子2:
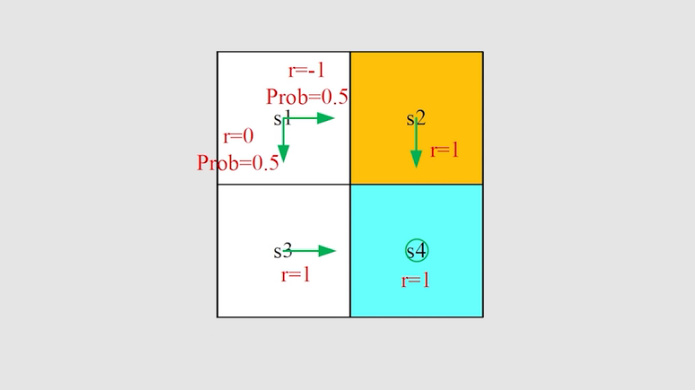
同理,得到每个状态的贝尔曼公式,如下:
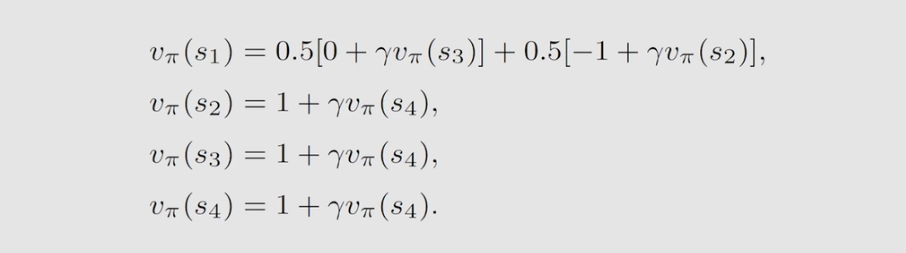
解得的结果如下:
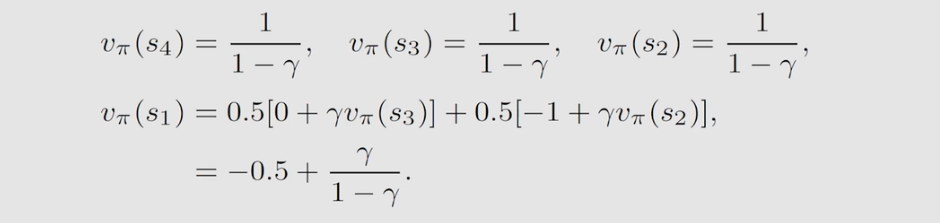
当
γ
=
0.9
γ=0.9
γ=0.9 则有:
v
π
(
s
1
)
=
8.5
v_π(s_1)=8.5
vπ(s1)=8.5
v
π
(
s
2
)
=
10
v_π(s_2)=10
vπ(s2)=10
v
π
(
s
3
)
=
10
v_π(s_3)=10
vπ(s3)=10
v
π
(
s
4
)
=
10
v_π(s_4)=10
vπ(s4)=10
表明这个策略没有之前的例1策略好。
.
贝尔曼公式:向量形式
贝尔曼公式在实际问题中这样的公式不止一组,把所有的式子联立就可以整理成向量形式。为了能够写成向量形式,需要对贝尔曼方程进行变形。其中
r
π
(
s
)
r_π(s)
rπ(s) 代表从当前状态出发所能得到的及时奖励的平均值,
p
π
(
s
′
∣
s
)
p_π(s'|s)
pπ(s′∣s) 表示从状态
s
s
s 到
s
′
s'
s′ 的概率。


为了区分,我们引入下标,得到的贝尔曼方程如下:

因此,我们可以得到如下形式:
其中
[
p
π
]
i
,
j
[p_π]_{i,j}
[pπ]i,j 代表的意思是矩阵
[
p
π
]
[p_π]
[pπ] 的第
i
i
i 行第
j
j
j 列的元素是从状态
s
i
s_i
si 跳到状态
s
j
s_j
sj 的概率

为了更好的理解上述的向量形式,我们通过一个例子进行说明:

现在考虑这两例子,已经给出策略(箭头),如下图,那么他的贝尔曼方程的矩阵形式怎么写呢?


.


贝尔曼公式:求解
我们知道,给出一个策略我们就会很容易列出其对应的贝尔曼方程,通过求解贝尔曼公式得到 state value ,这样的过程我们称为策略评估,策略评估是强化学习中非常关键的一步,也是最重要的工具,通过策略评估我们才会找出最优的策略。
如何求解贝尔曼公式,通常有矩阵法和迭代法两种方法
矩阵法!通过线性代数知识可轻易得到解的形式,但是在实际问题中我们并不常用,因为实际问题的矩阵空间很大,求解逆矩阵的计算量就会很大。

迭代法!通过随机给定一个初始值
v
0
v_0
v0 ,不断迭代可以得到一组序列 {
v
0
,
v
0
,
v
0
,
…
{v_0,v_0,v_0,…}
v0,v0,v0,…},当迭代次数
k
k
k 足够大时,那么得到的值就会接近真实值。

为了更好理解贝尔曼方程解的过程,我们给一个例子,如下如,设置的规则为
r
边界
=
r
陷阱
=
−
1
r_{边界}=r_{陷阱}=-1
r边界=r陷阱=−1,
r
终点
=
+
1
r_{终点}=+1
r终点=+1,
γ
=
0.9
γ=0.9
γ=0.9


我们可以发现,通过比较 state value ,表明策略1和策略2是比较好的,策略3和策略4是比较差的。
.
动作值 action value
state value 与 action value 的区别与联系:
状态值:是机械人从一个状态出发所得到的 return 平均值。
动作值:是机械人从一个状态出发并且选择了一个行为得到的 return 平均值。
本质上来说 state value 是 action value 的期望。
为什么我们要关心动作值?是因为强化学习中的策略指的就是在一个状态如何选择一个行为使得最后得到的状态值更大,而如何选择一个好的行为就需要用 action value 来判断。
动作值 action value 的定义如下:

从数学角度来看 state value 与 action value 的联系:

(2)式说明如果知道了动作值求平均就可以得到状态值。
(4)式说明如果知道了所有的状态值就可以得到动作值。
通过下列的例子,我们来理解 action value

我们可以很容易得到状态
s
1
s_1
s1 的 action value
q
π
(
s
1
,
a
2
)
=
−
1
+
γ
v
π
(
s
2
)
q_π(s_1,a_2)=-1+γv_π(s_2)
qπ(s1,a2)=−1+γvπ(s2)
虽然给出的策略是执行
a
2
a_2
a2 ,但是这个策略可能是不好的,需要重新选择策略时,需要计算其他的 action value 。同理,我们可以求出执行其他行为的动作值,如下:
q
π
(
s
1
,
a
1
)
=
−
1
+
γ
v
π
(
s
1
)
q_π(s_1,a_1)=-1+γv_π(s_1)
qπ(s1,a1)=−1+γvπ(s1)
q
π
(
s
1
,
a
3
)
=
0
+
γ
v
π
(
s
3
)
q_π(s_1,a_3)=0+γv_π(s_3)
qπ(s1,a3)=0+γvπ(s3)
q
π
(
s
1
,
a
4
)
=
−
1
+
γ
v
π
(
s
1
)
q_π(s_1,a_4)=-1+γv_π(s_1)
qπ(s1,a4)=−1+γvπ(s1)
q
π
(
s
1
,
a
5
)
=
0
+
γ
v
π
(
s
1
)
q_π(s_1,a_5)=0+γv_π(s_1)
qπ(s1,a5)=0+γvπ(s1)


![Midjourney|文心一格prompt教程[Text Prompt(上篇)]:品牌log、App、徽章、插画、头像场景生成,各种风格选择:科技风、运动风](https://img-blog.csdnimg.cn/img_convert/4d06f7942e86e7dde73e717e85ea69c3.png)