
typedef struct {
    ngx_radix_node_t  *root;
    ngx_pool_t        *pool;
    ngx_radix_node_t  *free;
    char              *start;
    size_t             size;
} ngx_radix_tree_t;

预备知识

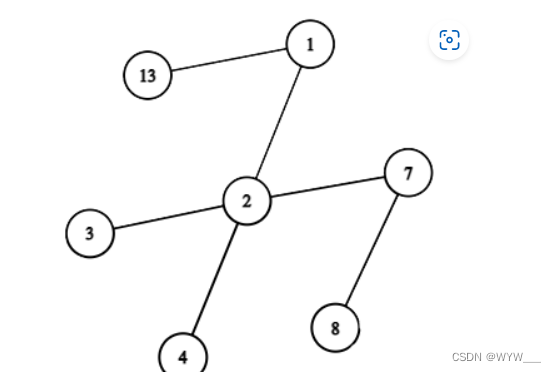
1.基数树也是一种二叉查找树,目前官方模块中仅geo模块使用了基数树.

2.ngx_radix_tree_t基数树要求存储的每个节点都必须以32位整型作为区别任意两个节点的唯一标识

3. 基数树的每个节点中可以存储的值只是 1 个指针，它指向实际的数据

4.基数树实际是按二进制位来建立树的

5.基数树具备二叉查找树的所有优点：基本操作速度快（如检索、插入、删除节点）、支

持范围查询、支持遍历操作等。但基数树不像红黑树那样会通过自身的旋转来达到平衡，基

数树是不管树的形态是否平衡的，因因此，它插入节点、删除节点的速度要比红黑树快得多

6.节点的key关键字已经决定了这个节点处于树中的位置。决定节点位置的方法很简单，先

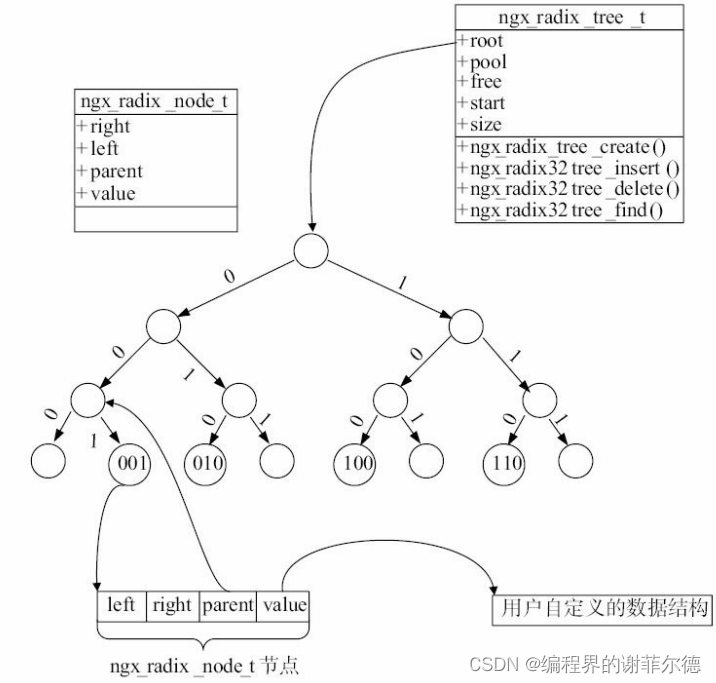
将这个节点的整型关键字转化为二进制，从左向右数这 32 个位，遇到 0时进入左子树，遇到1 时进入右子树。因此，ngx_radix_tree_t树的最大深度是32

基本数据结构

struct ngx_radix_node_s {
    ngx_radix_node_t  *right;
    ngx_radix_node_t  *left;
    ngx_radix_node_t  *parent;
    uintptr_t          value;
};


typedef struct {
    ngx_radix_node_t  *root;
    ngx_pool_t        *pool;
    ngx_radix_node_t  *free;
    char              *start;
    size_t             size;
} ngx_radix_tree_t;

结构成员分析：

节点:

value 字段指向用户自定义的、有意义的数据结构

树

root 根节点

pool 内存池

free 已分配内存中还未使用内存的首地址

start 已分配内存中还未使用的内存大小

size 已分配内存中使用的内存大小

内存布局：

操作函数

创建

ngx_radix_tree_t *ngx_radix_tree_create(ngx_pool_t *pool,
    ngx_int_t preallocate);

{
    uint32_t           key, mask, inc;
    ngx_radix_tree_t  *tree;

    tree = ngx_palloc(pool, sizeof(ngx_radix_tree_t));
    if (tree == NULL) {
        return NULL;

    tree->pool = pool;
    tree->free = NULL;
    tree->start = NULL;
    tree->size = 0;

    tree->root = ngx_radix_alloc(tree);
    if (tree->root == NULL) {
        return NULL;
    }

    tree->root->right = NULL;
    tree->root->left = NULL;
    tree->root->parent = NULL;
    tree->root->value = NGX_RADIX_NO_VALUE;
    //只创建结构体ngx_radix_tree_t,没有创建任何基数树节点*
    if (preallocate == 0) {
        return tree;
    }

    }
//根据下面的情况创建基数树节点*
f (preallocate == -1) {
        switch (ngx_pagesize / sizeof(ngx_radix_node_t)) {

        /* amd64 */
        case 128:
            preallocate = 6;
            break;

        /* i386, sparc64 */
        case 256:
            preallocate = 7;
            break;

        /* sparc64 in 32-bit mode */
        default:
            preallocate = 8;
        }
    }
mask = 0;
    inc = 0x80000000;

    while (preallocate--) {

        key = 0;
        mask >>= 1;
        mask |= 0x80000000;

        do {
            if (ngx_radix32tree_insert(tree, key, mask, NGX_RADIX_NO_VALUE)
                != NGX_OK)
            {
                return NULL;
            }

            key += inc;//当preallocate=0时，是最后一层，构建的节点个数为2^preallocate


        } while (key);
      inc >>= 1;
    }

    return tree;
}

函数解析:

1.pool是内存池指针 preallocate：预分配的基数树节点树如果传递的值为-1，那么将会根据当前操作系统中一个页面的大小来预分配基数树节点

#define NGX_RADIX_NO_VALUE   (uintptr_t) -1

* amd64上的6位(64位平台和4K页面)

* i386上的7位(32位平台和4K页面)

* 64位模式下sparc64上的7个比特位(8K页)

* 32位模式下sparc64上的8个比特位(8K页)

if (preallocate == -1) {
        switch (ngx_pagesize / sizeof(ngx_radix_node_t)) {

        /* amd64 */
        case 128:
            preallocate = 6;
            break;

        /* i386, sparc64 */
        case 256:
            preallocate = 7;
            break;

        /* sparc64 in 32-bit mode */
        default:
            preallocate = 8;
        }
    }

3.循环如下：

//加入preallocate=7,最终建的基数树的节点总个数为2^(preallocate+1)-1，每一层个数为2^(7-preallocate)
    //循环如下：
    //preallocate  =      7         6        5         4         3         2        1
    //mask(最左8位)=      10000000  11000000 11100000  11110000  11111000  11111100 11111110
    //inc          =     10000000  01000000 00100000  00010000  00001000  00000100 00000010
    //增加节点个数    =      2         4        8         16        32        64       128

插入

nginx的基数树只处理key值为整形的情况，所以每个整形被转化为二进制数，并且树的最大深度是32层。根据二进制位数从左到右，如果当前位为1，就向右子树，否则向左子树插入。当然有时候我们不想构建深度为32的基数树，nginx为此提供了一个掩码mask，这个掩码中1的个数决定了基数树的深度。

ngx_int_t
ngx_radix32tree_insert(ngx_radix_tree_t *tree, uint32_t key, uint32_t mask,
    uintptr_t value)
{
    uint32_t           bit;
    ngx_radix_node_t  *node, *next;

    bit = 0x80000000;从最左位开始，判断key
//10000000000000000000000000000000
    

    node = tree->root;
    next = tree->root;
//32位 一位一位来
//1->right
//0->left
    while (bit & mask) {
        if (key & bit) {
            next = node->right;

        } else { 
            next = node->left;
        }

        if (next == NULL) {
            break;
        }

        bit >>= 1;
        node = next;
    }
//判断是否初始化（是否为空）

    if (next) {
        if (node->value != NGX_RADIX_NO_VALUE) {
            return NGX_BUSY;
        }

        node->value = value;
        return NGX_OK;
    }

//如果next为中间节点，且为空，继续查找且申请路径上为空的节点
  
//比如找key=1000111，在找到10001时next为空，那要就要申请三个节点分别存10001,100011,1000111,
//1000111最后一个节点为key要插入的节点

    while (bit & mask) {
 next = ngx_radix_alloc(tree);
        if (next == NULL) {
            return NGX_ERROR;
        }

        next->right = NULL;
        next->left = NULL;
        next->parent = node;
        next->value = NGX_RADIX_NO_VALUE;

        if (key & bit) {
            node->right = next;

        } else {
            node->left = next;
        }

        bit >>= 1;
        node = next;
    }

    node->value = value;

    return NGX_OK;
}

删除节点

删除一个节点和插入节点的操作几乎一样，不过要注意两点：

1）如果删除的是叶子节点，直接从基数树中删除，并把这个节点放入free链表

2）如果不是叶子节点，把value值置为NGX_RADIX_NO_VALUE

ngx_int_t
ngx_radix32tree_delete(ngx_radix_tree_t *tree, uint32_t key, uint32_t mask)
{
    uint32_t           bit;
    ngx_radix_node_t  *node;
 
    bit = 0x80000000;
    node = tree->root;
    //根据key和掩码查找
    while (node && (bit & mask)) {
        if (key & bit) {
            node = node->right;
 
        } else {
            node = node->left;
        }
 
        bit >>= 1;
    }
 
    if (node == NULL) {//没有找到
        return NGX_ERROR;
    }
 
	//node不为叶节点直接把value置为空
    if (node->right || node->left) {
        if (node->value != NGX_RADIX_NO_VALUE) {//value不为空
            node->value = NGX_RADIX_NO_VALUE;//置空value
            return NGX_OK;
        }
 
        return NGX_ERROR;//value为空，返回error
    }
 
	//node为叶子节点，直接放到free区域
    for ( ;; ) {//删除叶子节点
        if (node->parent->right == node) {
            node->parent->right = NULL;//
 
        } else {
            node->parent->left = NULL;
        }
 
		//把node链入free链表
        node->right = tree->free;//放到free区域
        tree->free = node;//free指向node
        //假如删除node以后，父节点是叶子节点，就继续删除父节点，
		//一直到node不是叶子节点
        node = node->parent;
 
        if (node->right || node->left) {//node不为叶子节点
            break;
        }
 
        if (node->value != NGX_RADIX_NO_VALUE) {//node的value不为空
            break;
        }
 
        if (node->parent == NULL) {//node的parent为空
            break;
        }
    }
 
    return NGX_OK;
}

查找

这个函数是这四个函数中最简单的一个，就是根据key值查询，如果找到返回value值，没有找到返回NGX_RADIX_NO_VALUE。

uintptr_t
ngx_radix32tree_find(ngx_radix_tree_t *tree, uint32_t key)
{
    uint32_t           bit;
    uintptr_t          value;
    ngx_radix_node_t  *node;
 
    bit = 0x80000000;
    value = NGX_RADIX_NO_VALUE;
    node = tree->root;
 
    while (node) {
        if (node->value != NGX_RADIX_NO_VALUE) {
            value = node->value;
        }
 
        if (key & bit) {
            node = node->right;
 
        } else {
            node = node->left;
        }
 
        bit >>= 1;//往下层查找
    }
 
    return value;
}

申请节点

ngx_radix_alloc为基数树申请节点：

1）如果free链表不为空，直接从上面取下一个空闲节点

2）free链表为空，则申请一个节点

static void *
ngx_radix_alloc(ngx_radix_tree_t *tree)
{
    char  *p;
 
    if (tree->free) {//如果free中有可利用的空间节点
        p = (char *) tree->free;//指向第一个可利用的空间节点
        tree->free = tree->free->right;//修改free
        return p;
    }
 
    if (tree->size < sizeof(ngx_radix_node_t)) {//如果空闲内存大小不够分配一个节点就申请一页大小的内存
        tree->start = ngx_pmemalign(tree->pool, ngx_pagesize, ngx_pagesize);
        if (tree->start == NULL) {
            return NULL;
        }
 
        tree->size = ngx_pagesize;//修改空闲内存大小
    }
 
    //分配一个节点的空间
    p = tree->start;
    tree->start += sizeof(ngx_radix_node_t);
    tree->size -= sizeof(ngx_radix_node_t);
 
    return p;
}