Problem - 1593E - Codeforces

树是一个无定向的连接图，其中没有循环。这个问题是关于无根的树。一棵树的叶子是一个顶点，它最多与一个顶点相连。

园丁维塔利用n个顶点种了一棵树。他决定对这棵树进行修剪。为了做到这一点，他进行了一些操作。在一次操作中，他删除了树的所有叶子。

树的例子。

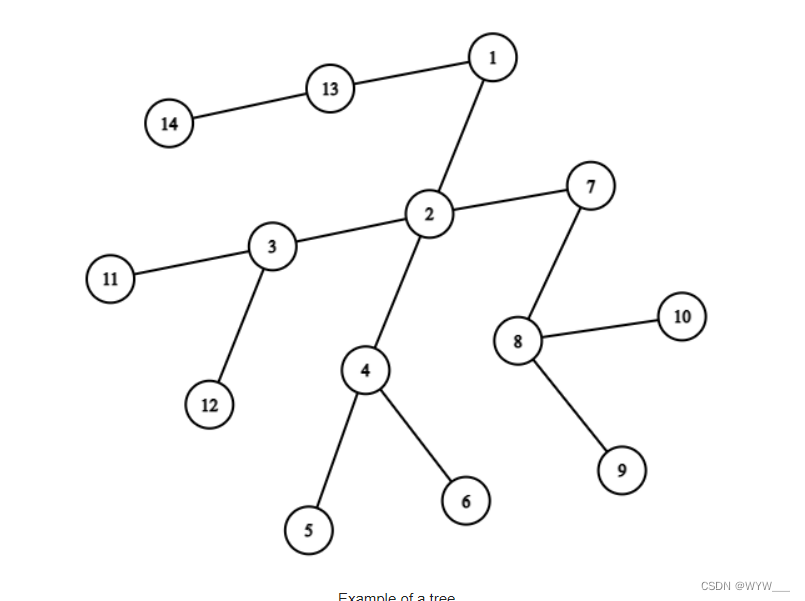
例如，考虑上图中所示的树。下图显示了对该树精确应用一个操作的结果。

 

 

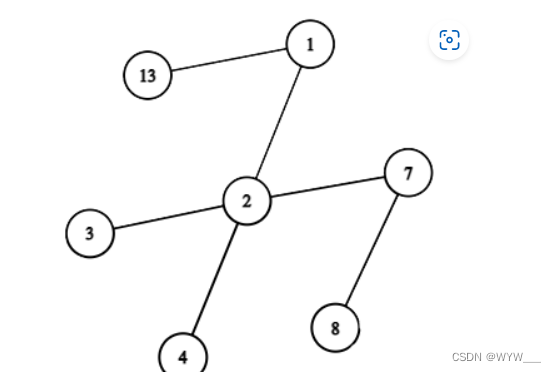
对树应用 "移除所有树叶 "操作的结果。
注意该操作的特殊情况。

对一棵空树（0个顶点）应用操作，不会改变它。
对有一个顶点的树应用操作，会删除这个顶点（这个顶点被当作叶子）。
对一棵有两个顶点的树进行操作，会删除这两个顶点（这两个顶点都被视为叶子）。
维塔利在树上依次应用了k个操作。还剩下多少个顶点？

输入
第一行包含一个整数t（1≤t≤104）--测试案例的数量。接着是t个测试用例。

每个测试用例前面都有一个空行。

每个测试用例由几行组成。测试用例的第一行包含两个整数n和k（1≤n≤4⋅105，1≤k≤2⋅105）--分别为树中顶点的数量和操作的数量。然后是n-1条线，每条线包含两个整数u和v（1≤u,v≤n, u≠v），描述一对由边连接的顶点。可以保证给定的图是一棵树，没有循环或多条边。

保证所有测试案例的n之和不超过4⋅105。

输出
对于每个测试用例，在单独的一行中输出一个整数--应用k操作后树中剩余的顶点数量。

例子
InputCopy
6

14 1
1 2
2 3
2 4
4 5
4 6
2 7
7 8
8 9
8 10
3 11
3 12
1 13
13 14

2 200000
1 2

3 2
1 2
2 3

5 1
5 1
3 2
2 1
5 4

6 2
5 1
2 5
5 6
4 2
3 4

7 1
4 3
5 1
1 3
6 1
1 7
2 1
输出拷贝
7
0
0
3
1
2
备注
第一个测试案例是在声明中考虑的。

第二个测试案例包含一棵有两个顶点的树。对它进行了200000次操作。第一个操作删除了所有两个顶点，其他操作不改变树。

在第三个测试案例中，给出了一棵有三个顶点的树。第一个操作的结果是，其中只剩下一个顶点（索引为2），第二个操作使树变空。

题解:
仔细想想每个叶子节点的入度都为1,每次删除所有的叶子节点,再找到入度为1的节点,这不就是拓扑排序吗(淦)

无非多了一个条件,进行找链长为k的停止

(写题时竟然完全没往这方面想)

#include<iostream>
#include<vector>
#include<queue>
#include<cstring>
#include<algorithm>
#include<string>
#include<map>
using namespace std;
#define int long long
char s[1000060];
vector<int> p[400050];
int cnt[400050];
int f[400040];
void solve()
{
//	ios::sync_with_stdio(false);
//	cin.tie(0);
//	cout.tie(0);
	int n,k;
	cin >> n >>k;
	for(int i = 1;i <= n;i++)
	{
		p[i].clear();
		cnt[i] = 0;
		f[i] = 0;
	}
	for(int i = 1;i < n;i++)
	{
		int x,y;
		cin >> x>>y;
		p[x].push_back(y);
		p[y].push_back(x);
		cnt[x]++;
		cnt[y]++;
	}
	if(n == 1)
	{
		if(k >= 1)
		{
			cout<<"0\n";
		}
		else
		{
			cout<<"1\n";
		}
		return ;
	}
	queue<pair<int,int>> q;
	for(int i = 1;i <= n;i++)
	{
		if(cnt[i] == 1)
		{
			q.push({i,1});
		}
	}
	while(q.size())
	{
		auto t = q.front();
		q.pop();
		f[t.first] = 1;
		for(auto j:p[t.first])
		{
			cnt[j] --;
			if(cnt[j] == 1)
			{
				if(t.second + 1 <= k)
				{
					q.push({j,t.second+1});
				}
			}
		}
	}
	int ans = 0;
	for(int i = 1;i <= n;i++)
	{
		if(!f[i])
		{
			ans ++;
		}
	}
	cout << ans<<"\n";
	
}
signed main()
{
	int t = 1;
	cin >> t;
	while(t--)
	{
		solve();
	}
}