CS 224N网址:Stanford CS 224N | Natural Language Processing with Deep Learning
Lecture1
PPT网址:PowerPoint Presentation (stanford.edu)
这一讲主要讲了NLP研究的对象,我们如何表示单词的含义,以及Word2Vec方法的基本原理。
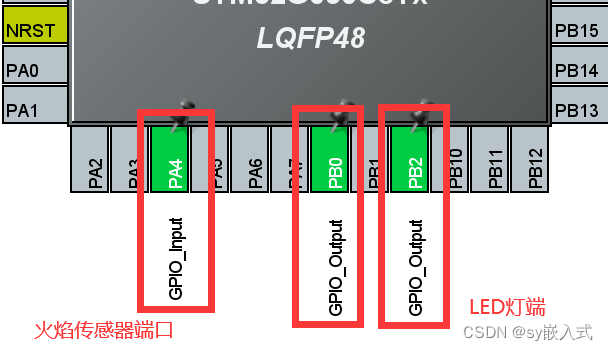
这里我们简单介绍一些Word2Vec方法的基本原理:人们认为,一个词往往与其上下文词的含义差不多,因此想要这些词的表达向量也差不多,我们定义一个窗口内的词为中心词和上下文词,如下图所示。

损失函数可写为:
-
J ( θ ) = − 1 T log L ( θ ) = − 1 T ∑ t = 1 T ∑ m ≤ j ≤ m j ≠ 0 log P ( w t + j ∣ w t ; θ ) J(\theta)=-\frac{1}{T} \log L(\theta)=-\frac{1}{T} \sum_{t=1}^T \sum_{\substack{m \leq j \leq m \\ j \neq 0}} \log P\left(w_{t+j} \mid w_t ; \theta\right) J(θ)=−T1logL(θ)=−T1∑t=1T∑m≤j≤mj=0logP(wt+j∣wt;θ)
- loss改写成对数是为了方便计算,这样所有的乘都会变成相加
-
为什么每个词要使用两个向量?(Lecture2的PPT中有提到,但不太详细)
- 为了方便数学计算
- softmax: P ( o ∣ c ) = exp ( u o T v c ) ∑ w ∈ V exp ( u w T v c ) P(o \mid c)=\frac{\exp \left(u_o^T v_c\right)}{\sum_{w \in V} \exp \left(u_w^T v_c\right)} P(o∣c)=∑w∈Vexp(uwTvc)exp(uoTvc)
- 可以注意到,在分母上,有这么一项 ∑ w ∈ V u w T v c \sum_{w \in V}u_w^Tv_c ∑w∈VuwTvc,如果我们将其对 v c v_c vc求导,结果为 ∑ w ∈ V u w \sum_{w \in V} u_w ∑w∈Vuw。然而,如果我们不使用两组向量,则该项应该写为 ∑ w ∈ V v w T v c \sum_{w \in V}v_w^Tv_c ∑w∈VvwTvc,这里需要注意的是, w w w 可能与 c c c 相同,我们可以写成 ∑ w ∈ V , w ≠ c v w T v c + v c T v c \sum_{w \in V ,w \ne c}v_w^Tv_c + v_c^Tv_c ∑w∈V,w=cvwTvc+vcTvc,对 v c v_c vc 求导,结果为 ∑ w ∈ V , w ≠ c v w + 2 v c \sum_{w \in V ,w \ne c}v_w + 2v_c ∑w∈V,w=cvw+2vc,这会导致求导结果不如使用两种向量得到的结果容易理解。
- 最终两个向量会很相似,但是不相同,我们取两个向量的平均来表达最终的word vector
- 具体推导:01 Introduction and Word Vectors - The Sun Also Rises
- 为了方便数学计算
Lecture2
PPT网址:cs224n-2023-lecture02-wordvecs2.pdf (stanford.edu)
Bag of words 模型:模型不考虑词的顺序,对一个词在不同位置的预测都是一样的
- Word2Vec的两种变体:
- Skip-grams:给定中心词来预测上下文单词(我们展示的Word2Vec model就是这种形式)
- Continuous Bag of Words(CBOW):通过上下文单词来预测中心词
可以用来更新的方法:
- Gradient Descent(GD):在所有样本上计算完梯度之后,再进行一次更新
- Stochastic Gradient Descent(SGD):每次使用单个样本进行更新
- Mini-batch Gradient Descent(MBGD):每次使用一批样本进行更新,介于上面两者之间
可以用来训练的 loss function:
- 朴素
softmax(简单,但是当类别比较多的时候,计算量很大) - 优化的变种,比如层次
softmax - 负采样(
negative sampling)
在上面,我们使用的loss function是朴素 softmax
-
J ( θ ) = − 1 T log L ( θ ) = − 1 T ∑ t = 1 T ∑ m ≤ j ≤ m j ≠ 0 log P ( w t + j ∣ w t ; θ ) J(\theta)=-\frac{1}{T} \log L(\theta)=-\frac{1}{T} \sum_{t=1}^T \sum_{\substack{m \leq j \leq m \\ j \neq 0}} \log P\left(w_{t+j} \mid w_t ; \theta\right) J(θ)=−T1logL(θ)=−T1∑t=1T∑m≤j≤mj=0logP(wt+j∣wt;θ)
-
P ( w t + j ∣ w t ; θ ) = P ( o ∣ c ) P(w_{t+j} |w_t;\theta) = P(o|c) P(wt+j∣wt;θ)=P(o∣c),这一项的分母计算量很大,因此在标准的
word2vec中,我们不采用这种形式,而是利用负采样方法 -
负采样的核心思想:训练二元逻辑回归来区分一个真对(中心词与上下文窗口中的词)和一些噪音对(中心词与一些随机的词)
-
负采样的 loss function:
- 最大化
J
t
(
θ
)
=
log
σ
(
u
o
T
v
c
)
+
∑
i
=
1
k
E
j
∼
P
(
w
)
[
log
σ
(
−
u
j
T
v
c
)
]
J_t(\theta)=\log \sigma\left(u_o^T v_c\right)+\sum_{i=1}^k \mathbb{E}_{j \sim P(w)}\left[\log \sigma\left(-u_j^T v_c\right)\right]
Jt(θ)=logσ(uoTvc)+∑i=1kEj∼P(w)[logσ(−ujTvc)]
- 我们在第一个对数中使两个词同时出现的概率最大化,在第二个对数中使噪声词的概率最小化
- k代表采样的负样本个数
- 这可以写成
J
neg-sample
(
u
o
,
v
c
,
U
)
=
−
log
σ
(
u
o
T
v
c
)
−
∑
k
∈
{
K
sampled indices
}
log
σ
(
u
k
T
v
c
)
J_{\text {neg-sample }}\left(\boldsymbol{u}_o, \boldsymbol{v}_c, U\right)=-\log \sigma\left(\boldsymbol{u}_o^T \boldsymbol{v}_c\right)-\sum_{k \in\{K \text { sampled indices }\}} \log \sigma\left(\boldsymbol{u}_k^T \boldsymbol{v}_c\right)
Jneg-sample (uo,vc,U)=−logσ(uoTvc)−∑k∈{K sampled indices }logσ(ukTvc)
- 利用概率分布 P ( w ) = U ( w ) 3 / 4 / Z P(w)=U(w)^{3/4} / Z P(w)=U(w)3/4/Z 来采样, U ( w ) U(w) U(w)是unigram分布
上面主要介绍了Word2Vec模型,它是一种基于local context window的预测模型(Direct prediction),对于学习word vector,还有另一类模型是count based global matrix factorization
- Direct Prediction优点是可以概括比相关性更为复杂的信息,缺点是对统计信息利用的不够充分
- Count based模型优点是训练快速,并且有效的利用了统计信息,缺点是对于高频词汇较为偏向,并且仅能概括词组的相关性
count based模型:构建一个词汇的共现矩阵,每一行是一个word,每一列是context。但是矩阵容易太大,我们希望word vector的维度不要太大,因此使用一些降维方法学习word的低维表示。
-
比较典型的是SVD
-
GloVe(Global Vectors):结合了local context window与(count based)词汇共现矩阵的方法
- 详细介绍可见:CS224N笔记(二):GloVe - 知乎 (zhihu.com)