libiosa语音信号处理

librosa是一个非常强大的python语音信号处理的第三方库，本文参考的是librosa的官方文档，本文主要总结了一些重要，对我来说非常常用的功能。学会librosa后再也不用python去实现那些复杂的算法了，只需要一句语句就能轻松实现。

先总结一下本文中常用的专业名词：sr：采样率、hop_length：帧移、overlapping：连续帧之间的重叠部分、n_fft：窗口大小、spectrum：频谱、spectrogram：频谱图或叫做语谱图、amplitude：振幅、mono：单声道、stereo：立体声

时域

读取音频

librosa.load(path, sr=22050, mono=True, offset=0.0, duration=None)

读取音频文件。默认采样率是22050，如果要保留音频的原始采样率，使用sr = None。

参数：

• path ：音频文件的路径。
• sr ：采样率，如果为“None”使用音频自身的采样率
• mono ：bool，是否将信号转换为单声道
• offset ：float，在此时间之后开始阅读(以秒为单位)
• 持续时间：float，仅加载这么多的音频(以秒为单位)

返回：

• y ：音频时间序列
• sr ：音频的采样率

重采样

librosa.resample(y, orig_sr, target_sr, fix=True, scale=False)

重新采样从orig_sr到target_sr的时间序列

参数：

• y ：音频时间序列。可以是单声道或立体声。
• orig_sr ：y的原始采样率
• target_sr ：目标采样率
• fix：bool，调整重采样信号的长度，使其大小恰好为\(\frac{len(y)}{orig\_sr}*target\_sr =t*target\_sr\)
• scale：bool，缩放重新采样的信号，以使y和y_hat具有大约相等的总能量。

返回：

• y_hat ：重采样之后的音频数组

读取时长

librosa.get_duration(y=None, sr=22050, S=None, n_fft=2048, hop_length=512, center=True, filename=None)

计算时间序列的的持续时间(以秒为单位)

参数：

• y ：音频时间序列
• sr ：y的音频采样率
• S ：STFT矩阵或任何STFT衍生的矩阵(例如，色谱图或梅尔频谱图)。根据频谱图输入计算的持续时间仅在达到帧分辨率之前才是准确的。如果需要高精度，则最好直接使用音频时间序列。
• n_fft ：S的 FFT窗口大小
• hop_length ：S列之间的音频样本数
• center ：布尔值
  • 如果为True，则S [:, t]的中心为y [t * hop_length]
  • 如果为False，则S [:, t]从y[t * hop_length]开始
• filename ：如果提供，则所有其他参数都将被忽略，并且持续时间是直接从音频文件中计算得出的。

返回：

• d ：持续时间(以秒为单位)

读取采样率

librosa.get_samplerate(path)

参数：

• path ：音频文件的路径
• 返回：音频文件的采样率

写音频

librosa.output.write_wav(path, y, sr, norm=False)

将时间序列输出为.wav文件

参数：

• path：保存输出wav文件的路径
• y ：音频时间序列。
• sr ：y的采样率
• norm：bool，是否启用幅度归一化。将数据缩放到[-1，+1]范围。

在0.8.0以后的版本，librosa都会将这个函数删除，推荐用下面的函数：

import soundfile
soundfile.write(file, data, samplerate)

参数：

• file：保存输出wav文件的路径
• data：音频数据
• samplerate：采样率

过零率

计算音频时间序列的过零率。

librosa.feature.zero_crossing_rate(y, frame_length = 2048, hop_length = 512, center = True)

参数：

• y ：音频时间序列
• frame_length ：帧长
• hop_length ：帧移
• center：bool，如果为True，则通过填充y的边缘来使帧居中。

返回：

• zcr：zcr[0，i]是第i帧中的过零率

y, sr = librosa.load(librosa.util.example_audio_file())
print(librosa.feature.zero_crossing_rate(y))
# array([[ 0.134,  0.139, ...,  0.387,  0.322]])

波形图

librosa.display.waveplot(y, sr=22050, x_axis='time', offset=0.0, ax=None)

绘制波形的幅度包络线

参数：

• y ：音频时间序列
• sr ：y的采样率
• x_axis ：str {'time'，'off'，'none'}或None，如果为“时间”，则在x轴上给定时间刻度线。
• offset：水平偏移(以秒为单位)开始波形图

import librosa.display
import matplotlib.pyplot as plt

y, sr = librosa.load(librosa.util.example_audio_file(), duration=10)
librosa.display.waveplot(y, sr=sr)
plt.show()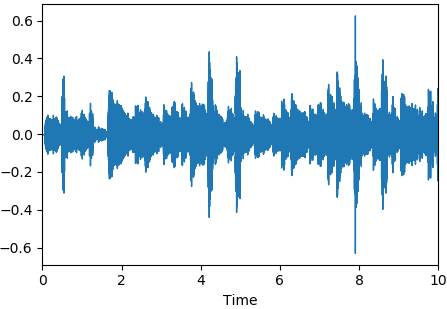

频域

短时傅里叶变换

librosa.stft(y, n_fft=2048, hop_length=None, win_length=None, window='hann', center=True, pad_mode='reflect')

短时傅立叶变换(STFT)，返回一个复数矩阵D(F，T)

参数：

• y：音频时间序列
• n_fft：FFT窗口大小，n_fft=hop_length+overlapping
• hop_length：帧移，如果未指定，则默认win_length / 4。
• win_length：每一帧音频都由window()加窗。窗长win_length，然后用零填充以匹配N_FFT。默认win_length=n_fft。
• window：字符串，元组，数字，函数 shape =(n_fft, )
  • 窗口(字符串，元组或数字)；
  • 窗函数，例如scipy.signal.hanning
  • 长度为n_fft的向量或数组
• center：bool
  • 如果为True，则填充信号y，以使帧 D [:, t]以y [t * hop_length]为中心。
  • 如果为False，则D [:, t]从y [t * hop_length]开始
• dtype：D的复数值类型。默认值为64-bit complex复数
• pad_mode：如果center = True，则在信号的边缘使用填充模式。默认情况下，STFT使用reflection padding。

返回：

• STFT矩阵，shape =(1 + \(\frac{n_{fft} }{2}\)，t)

补充一些复数知识(很重要)：
复数\(D(F,T)\)的几种表示形式：

• 实部、虚部(直角坐标系)：\(a+bj\) 　　 (\(a\)是实部，\(b\)是虚部)
• 幅值、相位(指数系)：\(re^{j\theta }\)　　(\(r\)是幅值，\(\theta\)是相角(弧度)，\(e^{j\theta }\)是相位)
• 极坐标表示法：\(r\angle \theta\)
• 指数系\(<-->\)指数坐标系：\(re^{j\theta }=r(cos\theta+jsin\theta)=rcos\theta+jrsin\theta\)

实部：\(a=rcos\theta\)， real = np.real(D(F, T))

虚部：\(b=rsin\theta\)， imag= np.imag(D(F, T))

幅值：\(r=\sqrt{a^2+b^2}\)， magnitude = np.abs(D(F, T)) 或 magnitude = np.sqrt(real**2+imag**2)

相角(以弧度为单位rad)：\(\theta=tan^{-1}(\frac{b}{a})\)或 \(\theta=atan2(b,a)\)。 angle = np.angle(D(F, T))

相角(以角度为单位deg)：\(deg = rad*\frac{180}{\pi}\)，\(\text{rad2deg}(\text{atan2}(b,a))\)。 deg = rad * 180/np.pi

相位： phase = np.exp(1j * np.angle(D(F, T)))

幅值和相位

librosa提供了专门将复数矩阵D(F, T)分离为幅值S和相位P的函数，D = S * P

librosa.magphase(D, power=1)

参数：

• D：经过stft得到的复数矩阵
• power：幅度谱的指数，例如，1代表能量，2代表功率，等等。

返回：

• D_mag：幅值D，
• D_phase：相位P， phase = exp(1.j * phi) ， phi 是复数矩阵的相位角 np.angle(D)

短时傅里叶逆变换

librosa.istft(stft_matrix, hop_length=None, win_length=None, window='hann', center=True, length=None)

短时傅立叶逆变换(ISTFT)，将复数值D(f,t)频谱矩阵转换为时间序列y，窗函数、帧移等参数应与stft相同

参数：

• stft_matrix ：经过STFT之后的矩阵
• hop_length ：帧移，默认为\(\frac{win_{length}}{4}\)
• win_length ：窗长，默认为n_fft
• window：字符串，元组，数字，函数或shape = (n_fft, )
  • 窗口(字符串，元组或数字)
  • 窗函数，例如scipy.signal.hanning
  • 长度为n_fft的向量或数组
• center：bool
  • 如果为True，则假定D具有居中的帧
  • 如果False，则假定D具有左对齐的帧
• length：如果提供，则输出y为零填充或剪裁为精确长度音频

返回：

• y ：时域信号

幅值转dB

librosa.amplitude_to_db(S, ref=1.0)

将幅度频谱转换为dB标度频谱。也就是对S取对数。与这个函数相反的是librosa.db_to_amplitude(S)

参数：

• S ：输入幅度
• ref ：参考值，幅值 abs(S) 相对于ref进行缩放，

返回：

• dB为单位的S，\(20*log_{10}(\frac{S}{ref})\)

功率转dB

librosa.core.power_to_db(S, ref=1.0)

将功率谱(幅值平方)转换为dB单位，与这个函数相反的是 librosa.db_to_power(S)

参数：

• S：输入功率
• ref ：参考值，振幅abs(S)相对于ref进行缩放

返回：

• dB为单位的S，\(10*log_{10}(\frac{S}{ref})\)

import librosa.display
import numpy as np
import matplotlib.pyplot as plt

y, sr = librosa.load(librosa.util.example_audio_file())
S = np.abs(librosa.stft(y))     # 幅值
print(librosa.power_to_db(S ** 2))
# array([[-33.293, -27.32 , ..., -33.293, -33.293],
#        [-33.293, -25.723, ..., -33.293, -33.293],
#        ...,
#        [-33.293, -33.293, ..., -33.293, -33.293],
#        [-33.293, -33.293, ..., -33.293, -33.293]], dtype=float32)

plt.figure()
plt.subplot(2, 1, 1)
librosa.display.specshow(S ** 2, sr=sr, y_axis='log')  # 绘制功率谱
plt.colorbar()
plt.title('Power spectrogram')
plt.subplot(2, 1, 2)
# 相对于峰值功率计算dB, 那么其他的dB都是负的，注意看后边cmp值
librosa.display.specshow(librosa.power_to_db(S ** 2, ref=np.max), sr=sr, y_axis='log', x_axis='time')   # 绘制对数功率谱
plt.colorbar(format='%+2.0f dB')
plt.title('Log-Power spectrogram')
plt.set_cmap("autumn")
plt.tight_layout()
plt.show()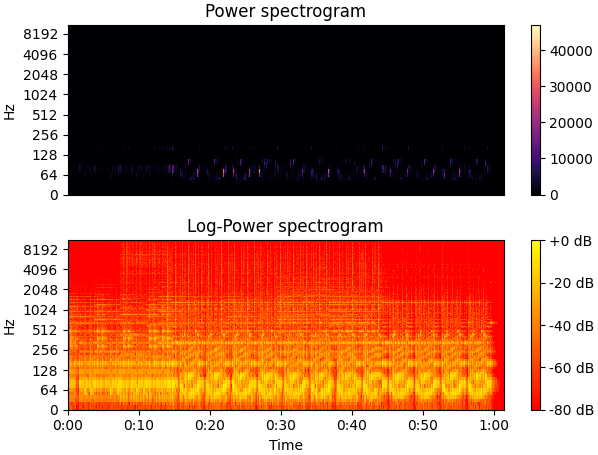

绘制频谱图

librosa.display.specshow(data, x_axis=None, y_axis=None, sr=22050, hop_length=512)

参数：

• data：要显示的矩阵
• sr ：采样率
• hop_length ：帧移
• x_axis 、y_axis ：x和y轴的范围

频率类型

• 'linear'，'fft'，'hz'：频率范围由FFT窗口和采样率确定
• 'log'：频谱以对数刻度显示
• 'mel'：频率由mel标度决定

时间类型

• time：标记以毫秒，秒，分钟或小时显示。值以秒为单位绘制。
• s：标记显示为秒。
• ms：标记以毫秒为单位显示。

所有频率类型均以Hz为单位绘制

import librosa.display
import numpy as np
import matplotlib.pyplot as plt

y, sr = librosa.load(librosa.util.example_audio_file())
plt.figure()

D = librosa.amplitude_to_db(np.abs(librosa.stft(y)), ref=np.max)
plt.subplot(2, 1, 1)
librosa.display.specshow(D, y_axis='linear')
plt.colorbar(format='%+2.0f dB')
plt.title('线性频率功率谱')

plt.subplot(2, 1, 2)
librosa.display.specshow(D, y_axis='log')
plt.colorbar(format='%+2.0f dB')
plt.title('对数频率功率谱')
plt.show()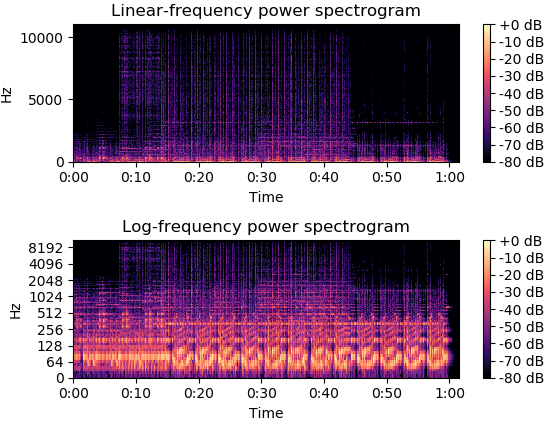

Mel滤波器组

librosa.filters.mel(sr, n_fft, n_mels=128, fmin=0.0, fmax=None, htk=False, norm=1)

创建一个滤波器组矩阵以将FFT合并成Mel频率

参数：

• sr ：输入信号的采样率
• n_fft ：FFT组件数
• n_mels ：产生的梅尔带数
• fmin ：最低频率(Hz)
• fmax：最高频率(以Hz为单位)。如果为None，则使用fmax = sr / 2.0
• norm：{None，1，np.inf} [标量]
  • 如果为1，则将三角mel权重除以mel带的宽度(区域归一化)。否则，保留所有三角形的峰值为1.0

返回：Mel变换矩阵

melfb = librosa.filters.mel(22050, 2048)
# array([[ 0.   ,  0.016, ...,  0.   ,  0.   ],
#        [ 0.   ,  0.   , ...,  0.   ,  0.   ],
#        ...,
#        [ 0.   ,  0.   , ...,  0.   ,  0.   ],
#        [ 0.   ,  0.   , ...,  0.   ,  0.   ]])
import matplotlib.pyplot as plt
plt.figure()
librosa.display.specshow(melfb, x_axis='linear')
plt.ylabel('Mel filter')
plt.title('Mel filter bank')
plt.colorbar()
plt.tight_layout()
plt.show()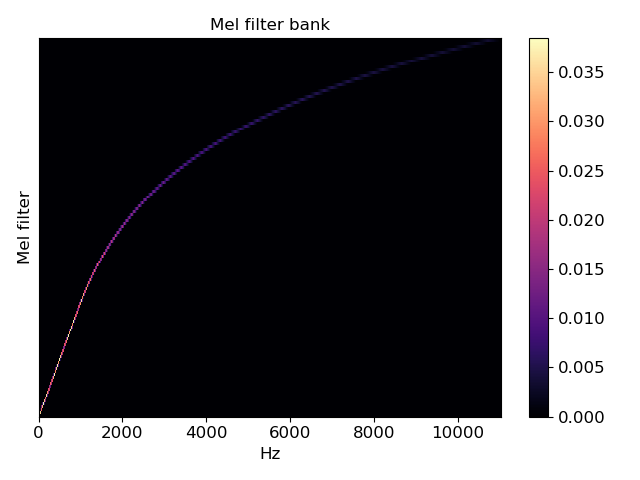

计算Mel频谱

librosa.feature.melspectrogram(y=None, sr=22050, S=None, n_fft=2048, hop_length=512, win_length=None, window='hann', center=True, pad_mode='reflect', power=2.0)

如果提供了频谱图输入S，则通过mel_f.dot(S)将其直接映射到mel_f上。

如果提供了时间序列输入y，sr，则首先计算其幅值频谱S，然后通过mel_f.dot(S ** power)将其映射到mel scale上 。默认情况下，power= 2在功率谱上运行。

参数：

• y ：音频时间序列
• sr ：采样率
• S ：频谱
• n_fft ：FFT窗口的长度
• hop_length ：帧移
• win_length ：窗口的长度为win_length，默认win_length = n_fft
• window ：字符串，元组，数字，函数或shape =(n_fft, )
  • 窗口规范(字符串，元组或数字)；看到scipy.signal.get_window
  • 窗口函数，例如 scipy.signal.hanning
  • 长度为n_fft的向量或数组
• center：bool
  • 如果为True，则填充信号y，以使帧 t以y [t * hop_length]为中心。
  • 如果为False，则帧t从y [t * hop_length]开始
• power：幅度谱的指数。例如1代表能量，2代表功率，等等
• n_mels：滤波器组的个数 1288
• fmax：最高频率

返回：Mel频谱shape=(n_mels, t)

import librosa.display
import numpy as np
import matplotlib.pyplot as plt

y, sr = librosa.load(librosa.util.example_audio_file())
# 方法一：使用时间序列求Mel频谱
print(librosa.feature.melspectrogram(y=y, sr=sr))
# array([[  2.891e-07,   2.548e-03, ...,   8.116e-09,   5.633e-09],
#        [  1.986e-07,   1.162e-02, ...,   9.332e-08,   6.716e-09],
#        ...,
#        [  3.668e-09,   2.029e-08, ...,   3.208e-09,   2.864e-09],
#        [  2.561e-10,   2.096e-09, ...,   7.543e-10,   6.101e-10]])

# 方法二：使用stft频谱求Mel频谱
D = np.abs(librosa.stft(y)) ** 2  # stft频谱
S = librosa.feature.melspectrogram(S=D)  # 使用stft频谱求Mel频谱

plt.figure(figsize=(10, 4))
librosa.display.specshow(librosa.power_to_db(S, ref=np.max), y_axis='mel', fmax=8000, x_axis='time')
plt.colorbar(format='%+2.0f dB')
plt.title('Mel spectrogram')
plt.tight_layout()
plt.show()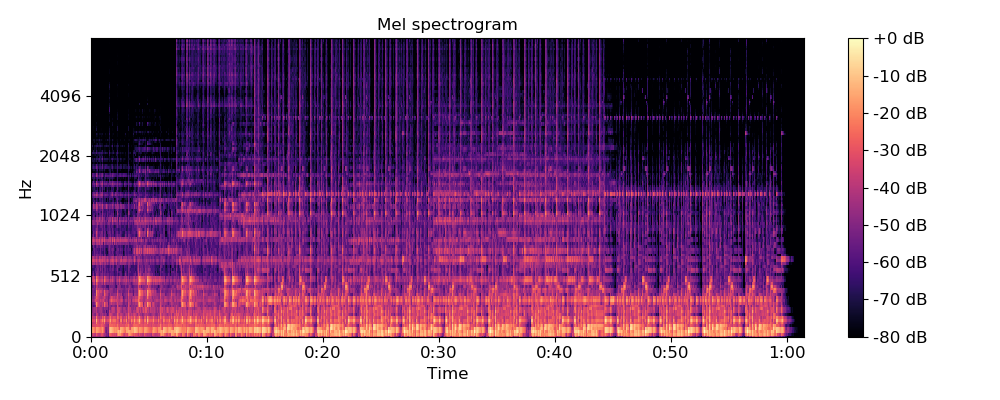

提取Log-Mel Spectrogram 特征

Log-Mel Spectrogram特征是目前在语音识别和环境声音识别中很常用的一个特征，由于CNN在处理图像上展现了强大的能力，使得音频信号的频谱图特征的使用愈加广泛，甚至比MFCC使用的更多。在librosa中，Log-Mel Spectrogram特征的提取只需几行代码：

import librosa

y, sr = librosa.load('./train_nb.wav', sr=16000)
# 提取 mel spectrogram feature
melspec = librosa.feature.melspectrogram(y, sr, n_fft=1024, hop_length=512, n_mels=128)
logmelspec = librosa.power_to_db(melspec)        # 转换到对数刻度

print(logmelspec.shape)        # (128, 65)

可见，Log-Mel Spectrogram特征是二维数组的形式，128表示Mel频率的维度(频域)，64为时间帧长度(时域)，所以Log-Mel Spectrogram特征是音频信号的时频表示特征。其中，n_fft指的是窗的大小，这里为1024；hop_length表示相邻窗之间的距离，这里为512，也就是相邻窗之间有50%的overlap；n_mels为mel bands的数量，这里设为128。

提取MFCC系数

MFCC特征是一种在自动语音识别和说话人识别中广泛使用的特征。关于MFCC特征的详细信息，有兴趣的可以参考博客https://www.cnblogs.com/LXP-Never/p/10918590.html。在librosa中，提取MFCC特征只需要一个函数：

librosa.feature.mfcc(y=None, sr=22050, S=None, n_mfcc=20, dct_type=2, norm='ortho', **kwargs)

参数：

• y：音频数据
• sr：采样率
• S：np.ndarray，对数功能梅尔谱图
• n_mfcc：int>0，要返回的MFCC数量
• dct_type：None, or {1, 2, 3} 离散余弦变换(DCT)类型。默认情况下，使用DCT类型2。
• norm： None or ‘ortho’ 规范。如果dct_type为2或3，则设置norm =’ortho’使用正交DCT基础。 标准化不支持dct_type = 1。

返回：

• M： MFCC序列

import librosa

y, sr = librosa.load('./train_nb.wav', sr=16000)
# 提取 MFCC feature
mfccs = librosa.feature.mfcc(y=y, sr=sr, n_mfcc=40)

print(mfccs.shape)        # (40, 65)

线性谱、梅尔谱、对数谱：经过FFT变换后得到语音数据的线性谱，对线性谱取Mel系数，得到梅尔谱；对线性谱取对数，得到对数谱。

参考

本文转载自作者：凌逆战，博客地址：https://www.cnblogs.com/LXP-Never/p/11561355.html