深度学习用于医学预后-第二课第四周1-4节-使用线性和基于树的模型构建风险评估模型

news2024/11/27 12:51:49

今天起进入到第四周课程的学习，使用线性和基于树的模型构建风险评估模型

风险分数

本周，你将学习建立和评估生存预测模型的策略，这些模型将使你能够比较个体患者的风险。您将学习两个这样的模型:Cox比例风险和生存树。最后，您将了解Harrell的c指数，它将允许您评估您将构建的生存模型的预测性能。

这将是非常激动人心的一周，因为它会把你们在这门课上学到的概念集合在一起。在本课中，您将学习与生存函数齐头并进的另外两个工具:风险函数和累积风险函数。您将看到生存、风险和累积风险函数都是相互关联的，可以帮助回答不同的问题。

风险

这节课中，我们来谈谈危险。到目前为止，我们已经研究了生存模型，其中我们有一个问题，在任意时刻 t 之后生存的概率是多少?

为了回答这个问题，我们看到了生存函数它告诉我们某个事件发生的时间在 t 之后的概率，我们可以用x轴表示生存函数，我们称其为t, y轴表示生存概率，随着时间的推移，它从1开始，然后趋于0。

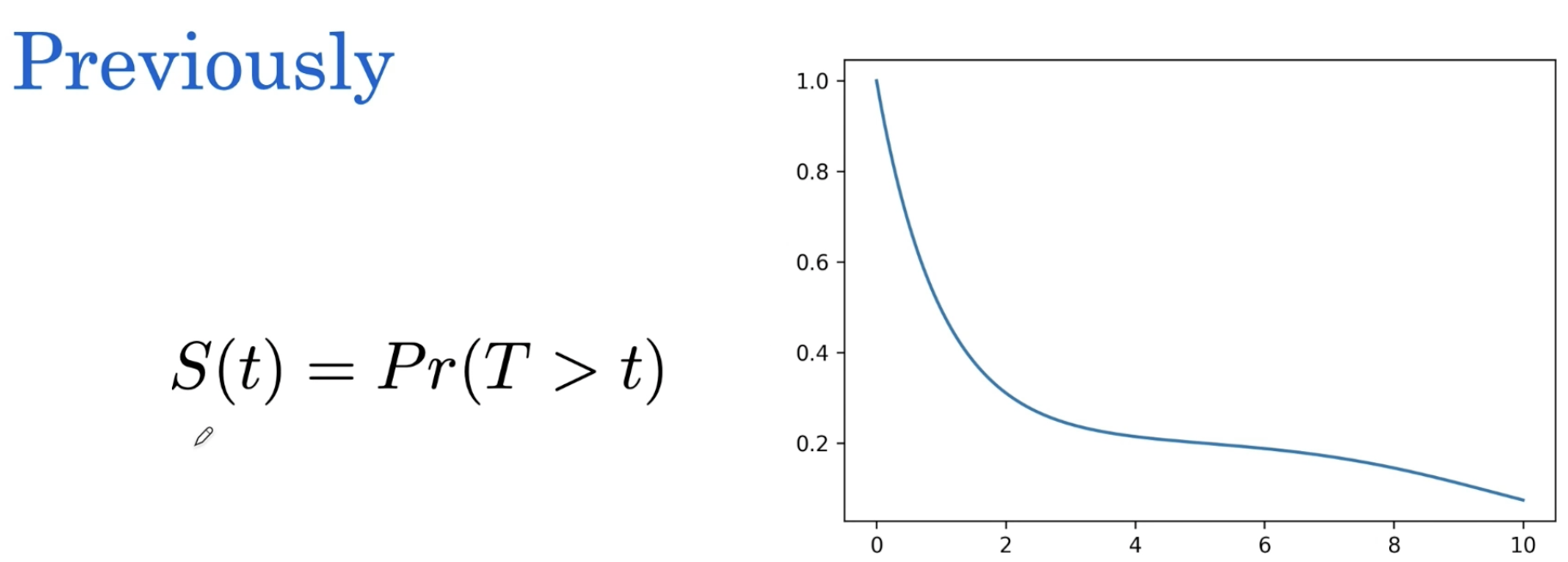
但假设我们现在感兴趣的是另一个问题，不是过了 t 时刻的生存概率是多少，而是病人的直接死亡风险是多少。我们可能想知道这个来了解一个病人是在第一年还是在第十年更危险，我们可以利用这个信息在病人最危险的时候通知治疗。

那么，如果病人活到了时间t，我们该如何表示他们的即时死亡风险呢?

这就是所谓的风险，风险用希腊字母“λ”表示。t的风险是事件发生的时间在t的概率

和生存函数一样，风险函数也可以用图形表示。

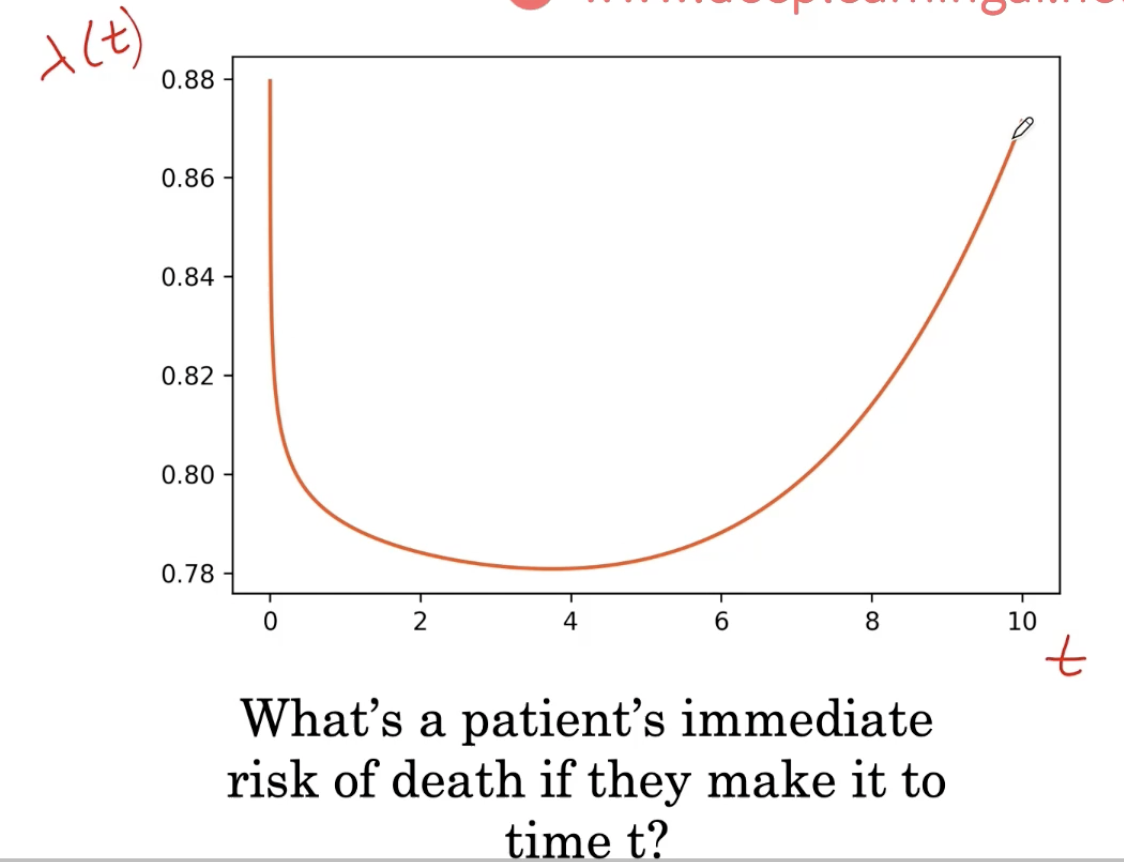
它告诉我们，随着时间的推移，特定时刻的风险是多少?注意这个形状，我们可以知道病人在任何时间点的瞬间死亡风险是什么。我们可以看到，它在0时是最高的，然后迅速下降到4，然后再次增加到10，危险程度与0时相似。

所以这让我们看到病人的风险左边区域高，中间区域不那么高，然后再增加。这就是所谓的浴盆曲线

在时间为零的时候，死亡的风险非常高，然后下降，然后随着时间的推移而增加。这是可能发生的，比如一些治疗，比如手术，并发症的风险可能很高，但随着时间的推移，它们会下降。但是，随着时间的推移，患者的风险会增加。

生存到风险

现在，风险函数实际上可以用来创建生存函数。他们是亲戚，我们不会过多地讨论他们的关系。但重要的是要明白有一个公式可以让我们从危险推导生存。

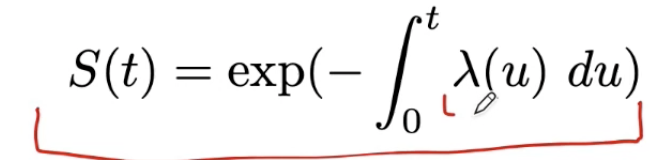
因此，我们可以用这个公式从危险曲线中得到相应的生存曲线。

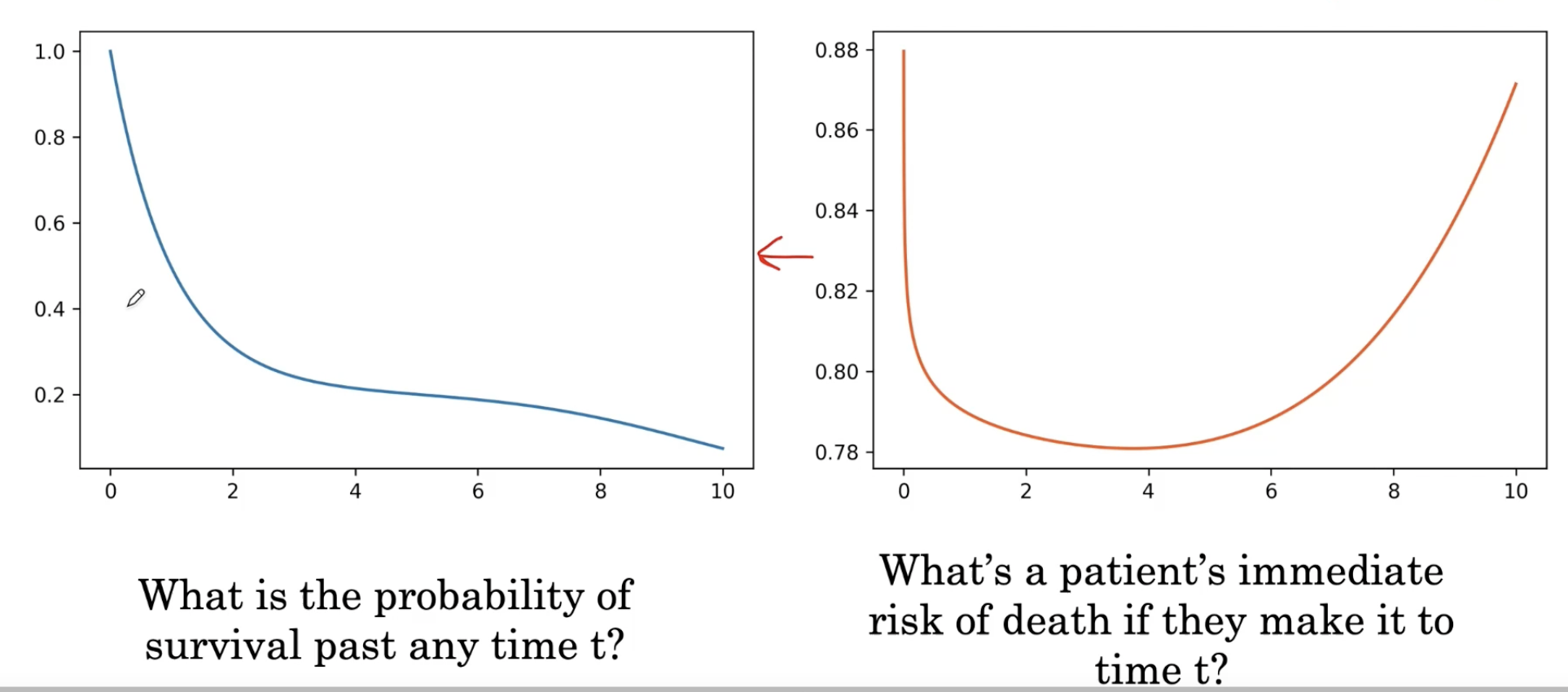
这是生存曲线对应危险曲线。我们看到，在任意时刻t之后生存的概率是多少，很容易。例如，如果我们想知道t=4后生存的概率，那么我们可以从图中读出它略高于0.2。同时，我们可以回答这样的问题，如果病人活到时刻t，他们的直接死亡风险是多少，通过观察t=4的风险并意识到时刻4的风险小于时刻8的风险。

这种关系是双向的，所以我们实际上也可以从生存曲线中推导出风险。同样，我们不用太担心给出它们关系的公式

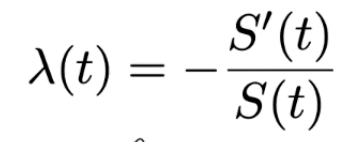
但你可以把这个公式解释为，如果年龄是t，那么危险就是死亡率。因此，使用这条生存曲线，我们可以生成相应的危险曲线。

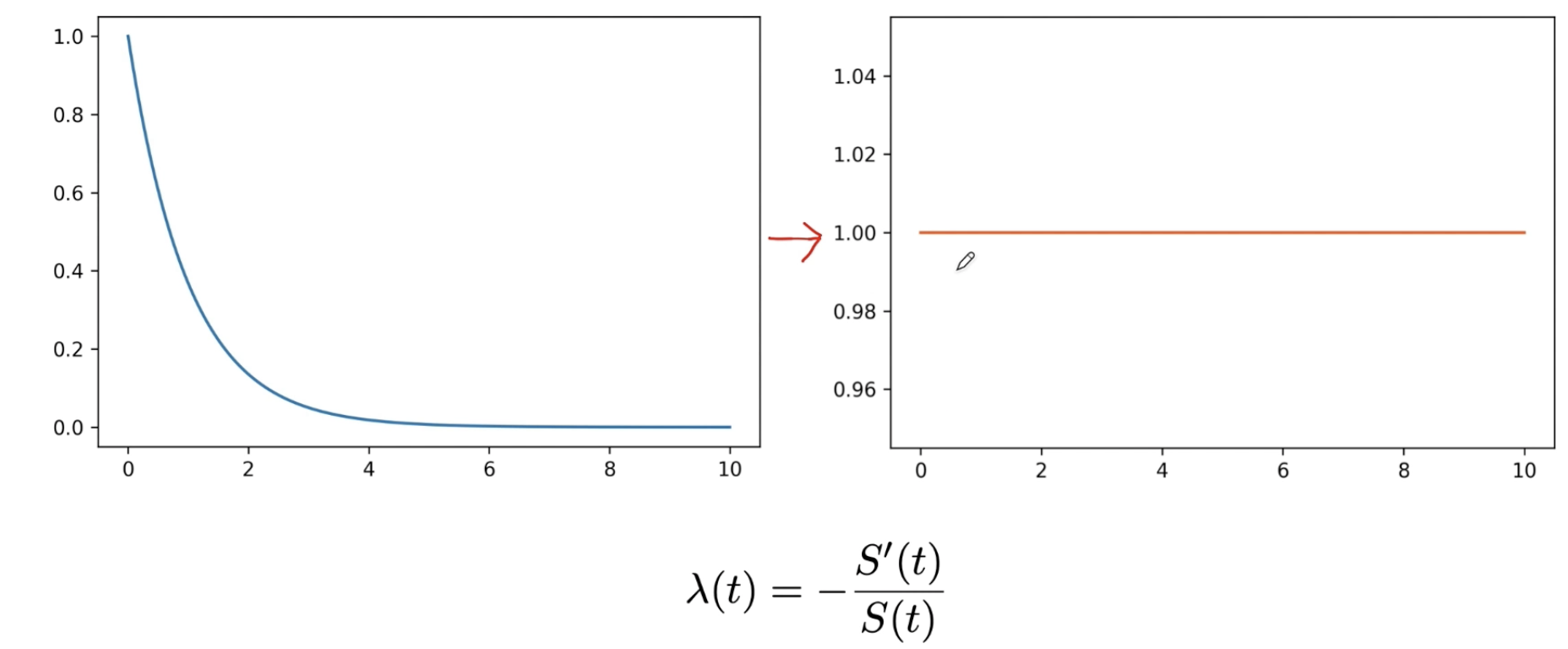
在这里我们可以看到这个病人群体的危险是一个恒定的函数这意味着即时死亡的风险在任何时候t都是恒定的;这是1。这是相应的生存曲线。我们现在已经把生存和危险看作是两个函数，一个可以用来推导另一个，反之亦然。

累积风险

到目前为止，我们已经通过生存函数来研究了在时间t之后的生存概率，以及在病人到达时间t时立即死亡的风险，即风险(hazard)。

现在，我们将探讨另一个问题，即病人在时间t之前的累积危险或累积风险(Cumulative Hazard)是多少？我们将用希腊字母“Λ”（大写的Lambda）来表示这个概念，记住小写字母“λ”表示hazard，而“Λ”表示在时间t之前的累积危险，即“Λ”(t)。

当然，病人在时间t之前的累积危险与他们在时间t的危险密切相关，它们之间的关系可以用以下方式表示

这意味着对于任何时间点t，我们都在查看它之前的所有时间点，并对它们进行求和。这就是当时间可以取离散值时的表达式，如0、1、2、3。我们还看到时间可以取从0到3或任何我们想要的连续数时的情况。

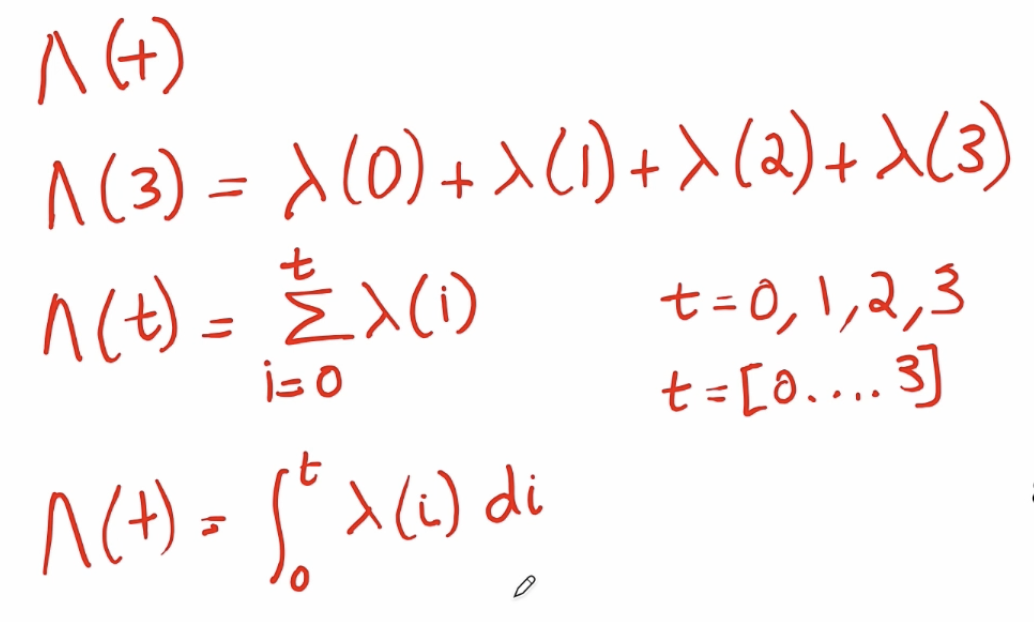
因此，我们将累积危险的连续扩展写为从0到t的lambda的积分。如果你以前没有接触过积分，不用太担心这个式子具体是怎么做的，只需要了解累积危险率会变成求和的形式，而这个公式用来表示时间是连续变量时的情况。

我们先前已经看到风险曲线，y轴表示的瞬时风险，x轴表示时间。我们可以使用这个危险曲线来告诉我们对应的累积危险曲线将是什么样子，使用我们之前看到的公式。再次强调，如果你以前没有接触过积分，不用太担心这个公式做了什么，它只是一种沿着时间轴求和危险率的方式。

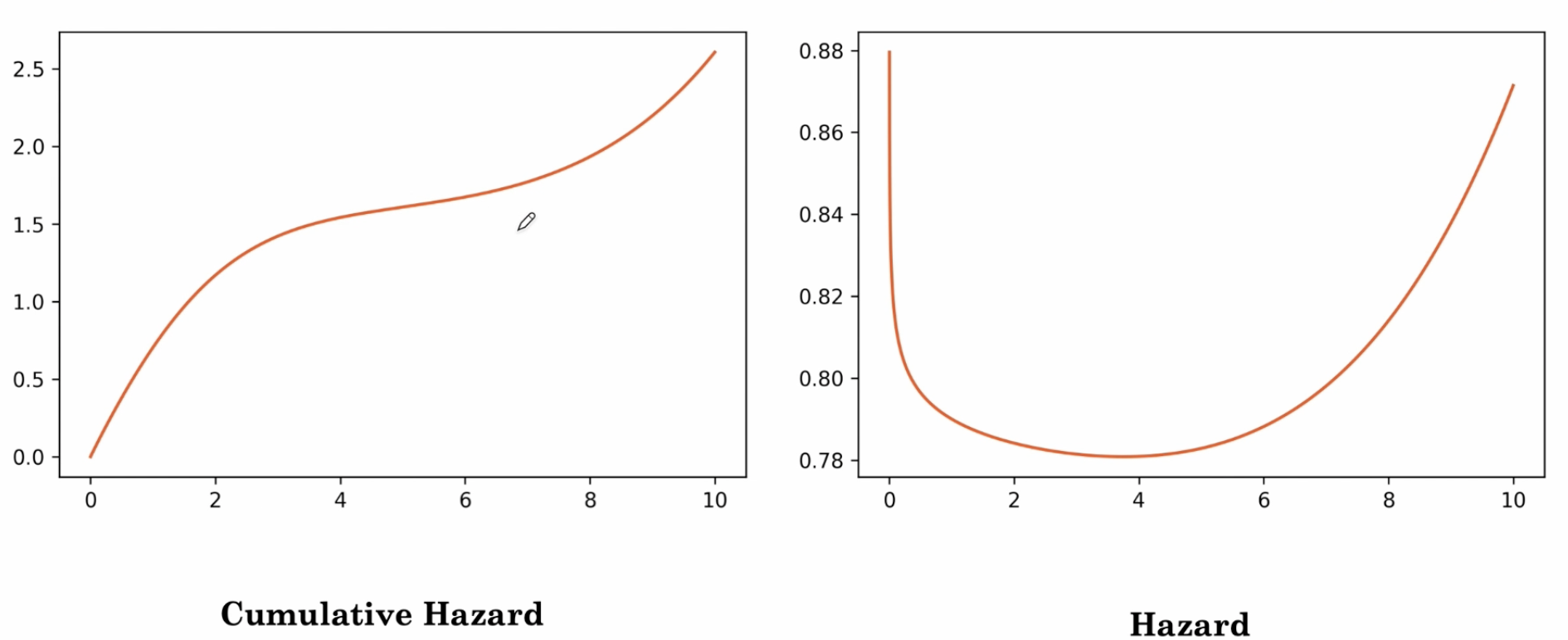
因此，这是一个相应的累积危险率，告诉我们病人随着时间累积的风险如何变化。

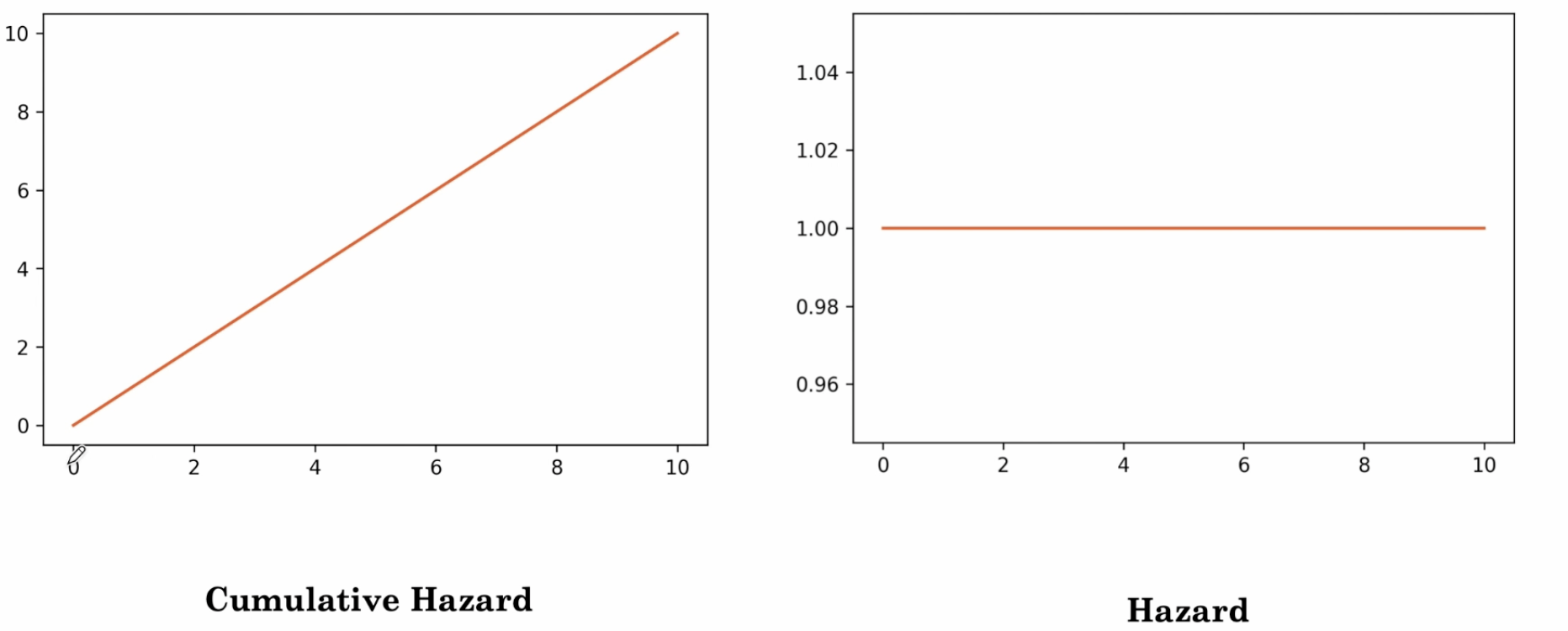
这是一个恒定的危险曲线，因此我们可以看到随着时间的推移，危险并没有改变，其相应的累积危险曲线如下所示；你可以看到，直线上升，我们正在对时间维度进行求和。