ZC序列的定义

ZC序列有两个重要的参数：

1. 根索引（root index）$q=1,2,\cdots ,N_{zc}-1$
2. ZC序列的长度$N_{zc}$，一定得是奇数（常常是质数）

给定上述两个参数，第$q$个ZC序列为：
$$s_q[n]=\exp \left[-j\pi q\frac{n(n+1)}{N_{zc}}\right],n=0,1,2,\cdots ,N_{zc}-1$$

注意到，每个ZC序列的长度为$N_{zc}$，而ZC序列的序列空间大小为$N_{zc}-1$（即一共有$N_{zc}-1$个ZC序列）。

与ZC序列相关的一些定义

（1）循环移位（cyclic shifts / circular shift）: simply the rotation of a finite length sequence.
给定一个长度为$N$的有限长序列$x[n]$，其$m$次循环移位为
$$x^m[n]=x[(n+m)\text{ mod }N],m=0,1,2,\cdots ,N-1$$

一共有$N$个循环移位序列（包含本身）。

（2）循环自相关 / 周期自相关(cyclic/periodic autocorrelation)：长度为$N$的有限长序列$x[n]$的循环自相关为：
$$R_{xx}[\tau ]=\sum _{n=0}^{N-1}{x}^{\ast }[n]x^{\tau }[n],\tau =0,1,2,\cdots ,N-1$$

归一化的循环自相关（normalized cyclic auto correlation）为
$${\bar{R}}_{xx}[\tau ]=\frac{1}{N}{R}_{xx}[\tau ]$$
显而易见，${\bar{R}}_{xx}[0]=1$，${\bar{R}}_{xx}[\tau \ne 0]\le 1$。
（3）循环自相关 / 周期互相关(cyclic/periodic corss correlation)：给定长度为$N$的两个有限长序列$x[n]$和$y[n]$，它们的循环互相关定义为
$$R_{xy}[\tau ]=\sum _{n=0}^{N-1}{x}^{\ast }[n]y^{\tau }[n],\tau =0,1,2,\cdots ,N-1$$
类似地，我们可以定义归一化的循环互相关
$${\bar{R}}_{xy}[\tau ]=\frac{1}{N}{R}_{xy}[\tau ]$$

一般地，我们把${\bar{R}}_{xy}[0]$称为两个序列的互相关(“cross correlation”)。

ZC序列的重要性质

（1）性质1：恒包络，即等模

（2）性质2：Zero Cyclic Auto correlation
一个ZC序列的循环自相关是最优的，因为对于所有的非零移位序列，与原序列的自相关都等于0，即
$$R_{xx}[\tau ]=\sum _{n=0}^{N-1}{s}^{\ast }[n{]}_q{s}_q^{\tau }[n]=N_{zc}\delta [\tau ]$$

有时，我们会将上述两个性质合并，称之为Constant Amplitude Zero Autocorrelation (CAZAC)，ZC序列有时也被称为CAZAC序列。

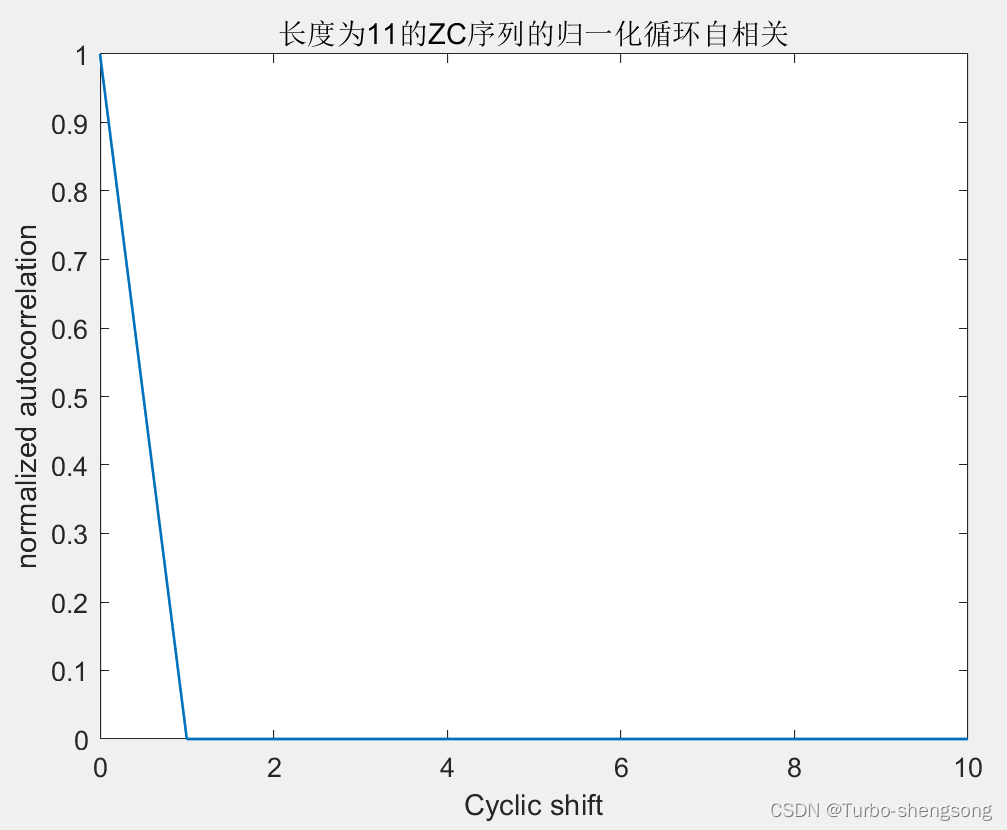
Seq1 = zadoffChuSeq(1,11);
haha = ones(11,1);
for i =2:11
	Seq_i = circshift(Seq1,[1,i]);
	haha(i) = abs(dot(Seq1, Seq_i))/sqrt(11);
end
figure; plot(0:10,haha)

（3）性质3：Fixed Cyclic Cross-Correlation

对相同长度的两个ZC序列，即一个序列的root index为$q_1$，另一个序列的root index为$q_2$，且$q_1\ne q_2$，那么两个序列的归一化循环互相关值正好等于$1/\sqrt{N_{zc}}$。这里一般假设$N_{zc}$是质数，或者更一般地，认为$|q_1-q_2|$与$N_{zc}$互质。（This is in fact the optimal cross-correlation for two any sequences with the optimal autocorrelation defined above. So it is somewhat remarkable that ZC sequences provided $N_{zc}$ is a prime number, can furnish $N_{zc}-1$ of such sequences. Note that if $N_{zc}$ is not a prime number, the $q_1-q_2$ constraint reduces the number of “good” sequences, which is why prime numbers are generally preferred.）

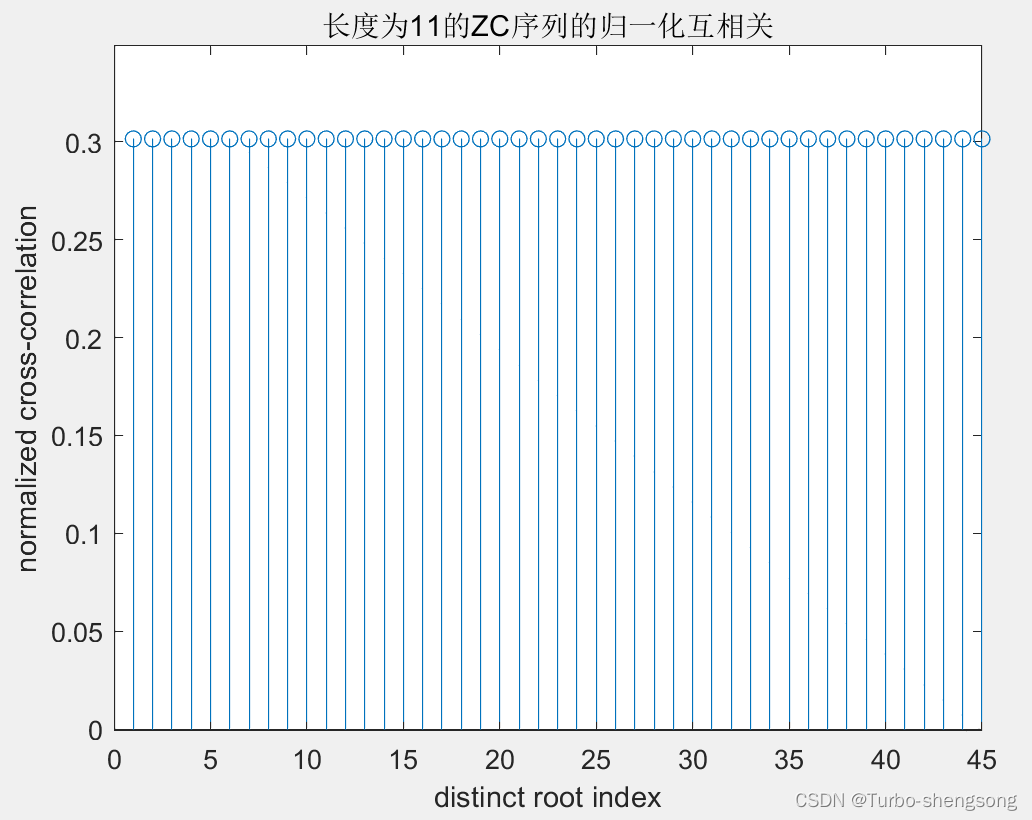
haha = [];
for i = 1: 10
	for j = (i+1) : 10
		if i < j
			Seqi = zadoffChuSeq(i,11); 
			Seqj = zadoffChuSeq(j,11); 
			cross_corr = abs(dot(Seqi, Seqj))/11;
			haha = [haha, cross_corr];
		end
	end
end
figure;stem(haha)

另外，性质2和性质3还说明了：

1. 相同root index的两个ZC序列彼此正交
2. 不同root index的两个ZC序列彼此不满足正交性

生成root index为1，长度为839的ZC序列Seq1，以及对Seq1循环移位10位的序列Seq2，Seq1与Seq2满足正交性。

Seq1 = zadoffChuSeq(1,839);
Seq2 = circshift(Seq1,[1,10]);

（4）性质4：The DFT or IDFT of a ZC sequence is a ZC sequence

ZC序列的长度不是质数时

一个任意长度的ZC序列可以通过【将长度为质数的ZC序列进行“循环扩展(cyclic extension)”和“截断(truncated)”】来构造。但上述性质2，3将不再严格保留，只是这种损失也许是系统可以容忍的。

假设我们要构造长度为$N_{sf}$的ZC序列（sf: spreading factor），有以下两种方式：

1. 循环扩展（cyclic extension）
   $$z_q[n]=s_q[n\text{ mod }{N}_{zc}],n=0,1,\cdots ,N_{sf}-1$$

其中$N_{zc}$是小于等于序列长度$N_{sf}$的最大质数。

2. 截断（truncated）
   构造$N_{zc}(\ge N_{sf})$的ZC序列，然后截断为$N_{sf}$长的序列。

以长度为12的ZC序列为例

因为LTE和5G NR的一个资源块，即1RB，常常包含12个子载波，因此长度为12的ZC序列是在这些标准中经常被使用到。长度为$N_{sf}=12$的ZC序列是基于$N_{zc}=11$进行循环扩展构造的。

尚未循环移位的两个ZC序列，root index分别为$q=1,4$为（经过循环扩展之后）
$$\begin{array}{rl}{\mathbf{z}}_1^{(0)}& =\exp \left(j\pi /11\cdot \left[0,-2,-6,10,2,-8,2,10,-6,-2,0,0\right]\right)\\ {\mathbf{z}}_4^{(0)}& =\exp \left(j\pi /11\cdot \left[0,-8,-2,-4,8,-10,8,-4,-2,-8,0,0\right]\right)\end{array}$$

包括上述两个序列在内的所有11个长度为12的ZC序列，它们的归一化循环自相关不再是delta函数，并且每个序列的循环自相关也不再相同，如下图所示：

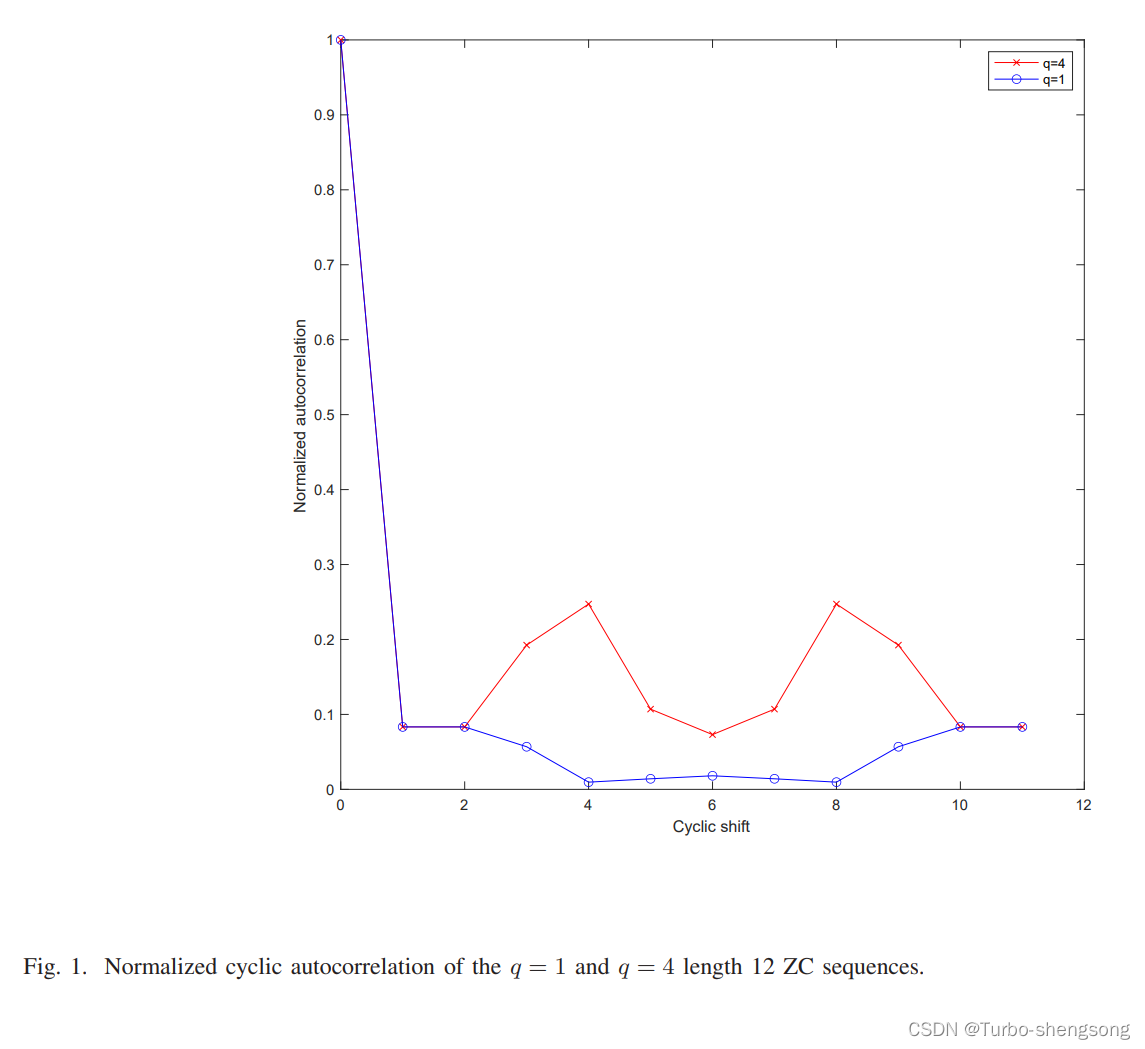
ZC序列在LTE和5G NR中的应用

(1) Initial downlink synchronization

这是UE要与BS建立连接的第一步，同步（synchronization）不仅包括UE获取BS的时钟信息（BS timing?），出于下一步进行连接的必要性，还包括了一些其他关键信息。Specially, the Primary Synchronization Sequence (PSS) is based on a $N_{zc}=63$ sequence, and values $q=29,34,25$ are used (a different value of $q$ for each sector, usually).

(2) Random access

具体来讲，是关于UE如何接入到BS？因为当前UE尚未接入到BS，BS就不会调度时频资源（time/frequency slot）给UE进行上行数据传输。因此，上行随机接入信道（uplink random access channel）应该足够健壮到，可以支撑很多UEs同行进行传输(at slightly different timing offsets)：A perfect setting for ZC sequences which have both strong shifted cross-correlation properties.

Specially, the Physical Random Access Channel uses $N_{zc}=839$ for the long preamble and $N_{zc}=139$ for the short preamble, in both LTE and 5G NR.

(3) Uplink control information

The Physical uplink control channel (PUCCH) is used bu the UEs to convey channel state information and ACK/NAKs, as well as requests to transmit. All the UEs share the PUCCH, so they periodically use it and also benefit from the use of spreading code to allow multiple UEs to send control information at the same time and frequency.

In LTE, there are 4 PUCCH formats: 0, 1, 2, and 3. ZC sequences (length 12, extended from Nzc = 11
sequences as in the above example) are used for all but format 3 (a supplemental format for use in
carrier aggregation).

In 5G NR, there are 5 PUCCH formats. ZC sequences (length 12) are used for formats 0 and 1.

(4) Uplink reference signals (pilot signals)

Uplink reference symbols are utilized by the BS for channel
estimation, synchronization, and are necessary for demodulating the UE’s data transmission. In particular
they are used for the Sounding Reference Symbols (SRS), which are sent periodically when the UE is
not transmitting data, as well as the Demodulation Reference Symbols (DM-RS) which are embedded
with data transmissions to aid with precise channel estimation.

In LTE and 5G NR, length Nzc = 31 ZC sequences are cyclically extended in the frequency domain
to achieve length 36 sequences for SRS transmissions.

As far as the DM-RS, whenever SC-FDMA is used, then the DM-RS are length 12 extended ZC
sequences. This is always the case in the LTE uplink. In 5G NR, the uplink can be either OFDMA or
SC-FDMA. When the 5G NR uplink uses OFDMA, then a Gold code (based on 2 maximal length PN
codes) is used instead of a ZC sequence.

参考

[1] A Primer on Zadoff Chu Sequences