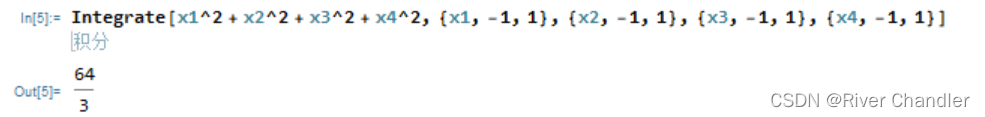计算物理专题：高维Romberg数值积分方法

news2024/9/21 4:29:33

有话无话，先上代码，正确与否，先给结论，可信有无，先出文献
计算物理，傅哥最强
- 真计算还得看SCU物拔（不是）（狗头）（骄傲）
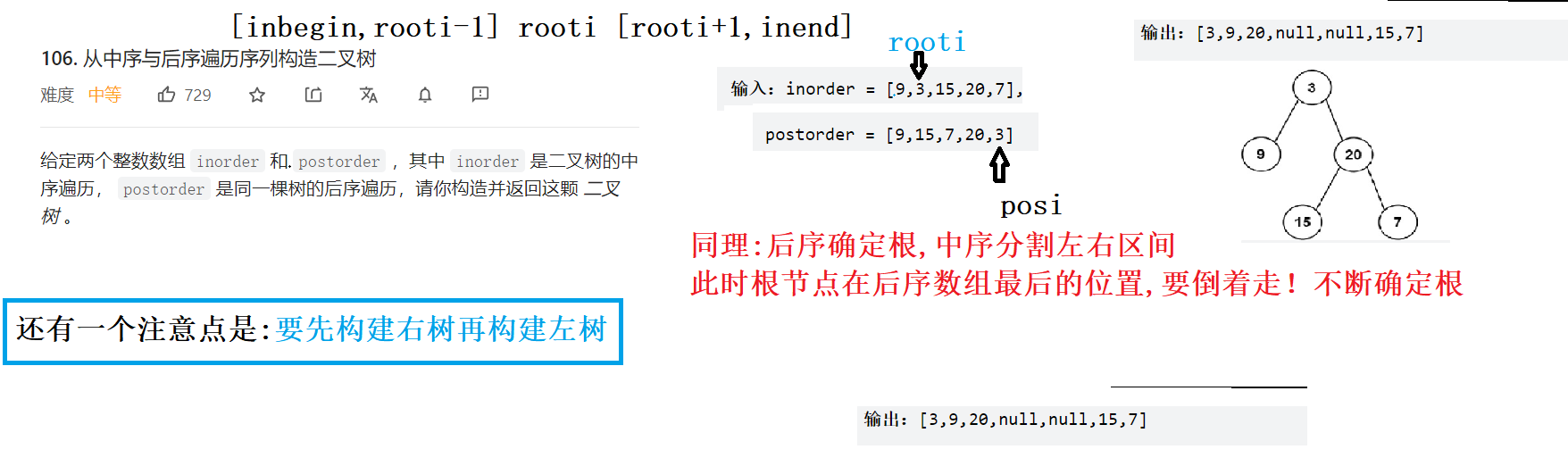
这种方法的思想是利用插值公式来构造高精度的积分公式，然后用递归的方式来增加精度。它的主要优点是精度高，收敛迅速，并且非常适合计算高维积分。
- 接着，我们将这些子区间合并成更大的区间，然后在这些区间上再次构造级别为 $k+1$ 的高精度插值公式，计算出积分值。通过递归的方式，我们可以得到不同级别的积分值。最终，将这些积分值代入级别最高的插值公式中，就可以得到所求积分的高精度近似值。

示例代码

十一维数值积分
友情提示：不要运行哦，你的笔记本算不出来的。。。。。
- 这个和博主的编码能力无关，就是算不出来，不要杠，杠你就输了
- 这个是随机内存的问题，高维积分方法不能出这个问题

def f(x,y,z,w,u,v,i,o,p,k,l):
    return x**2 + y**2 + z**2 +\
           w**2 + u**2 + v**2 +\
           i**2 + o**2 + p**2 +\
           k**2 + l**2
    


def romberg_11d(f,x1,x2,y1,y2,z1,z2,\
                 w1,w2,u1,u2,v1,v2,\
                 i1,i2,o1,o2,p1,p2,\
                 k1,k2,l1,l2,\
                 eps=1e-6,n=50):

    def trapezoid(f,a,b,n):
        h = (b - a) / float(n)
        s = 0.5*(f(a) + f(b))
        for i in range(1, n):
            s += f(a + i*h)
        return h*s
    
    def romberg(f,a,b,eps=1e-6,n=50):
        R = [[0]*(n+1) for i in range(n+1)]
        for i in range(1, n+1):
            h = float(b-a)/(2**i)
            R[i][1] = trapezoid(f, a, b, 2**(i-1))
            for j in range(2, i+1):
                R[i][j] = (4**(j-1)*R[i][j-1]-R[i-1][j-1])/(4**(j-1)-1)
            if abs(R[i][i]-R[i-1][i-1]) < eps:
                return R[i][i]
        raise ValueError('romberg integration failed to converge')

    def integrand_l(x,y,z,w,u,v,i,o,p,k):
        return romberg(lambda l:f(x,y,z,w,u,v,i,o,p,k,l),l1,l2,eps,n)

    def integrand_k(x,y,z,w,u,v,i,o,p):
        return romberg(lambda k:integrand_l(x,y,z,w,u,v,i,o,p,k),k1,k2,eps,n)

    def integrand_p(x,y,z,w,u,v,i,o):
        return romberg(lambda p:integrand_k(x,y,z,w,u,v,i,o,p),p1,p2,eps,n)

    def integrand_o(x,y,z,w,u,v,i):
        return romberg(lambda o:integrand_p(x,y,z,w,u,v,i,o),o1,o2,eps,n)

    def integrand_i(x,y,z,w,u,v):
        return romberg(lambda i:integrand_o(x,y,z,w,u,v,i),i1,i2,eps,n)
    
    def integrand_v(x,y,z,w,u):
        return romberg(lambda v:integrand_i(x,y,z,w,u,v),v1,v2,eps,n)

    def integrand_u(x,y,z,w):
        return romberg(lambda u:integrand_v(x,y,z,w,u),u1,u2,eps,n)

    def integrand_w(x,y,z):
        return romberg(lambda w:integrand_u(x,y,z,w),w1,w2,eps,n)

    def integrand_z(x,y):
        return romberg(lambda z:integrand_w(x,y,z),z1,z2,eps,n)

    def integrand_y(x):
        return romberg(lambda y:integrand_z(x,y),y1,y2,eps,n)

    return romberg(lambda x:integrand_y(x),x1,x2,eps,n)

#x,y,z,w,u,v,i,o,p,k,l
result = romberg_11d(f,-1,1,-1,1,-1,1,\
                       -1,1,-1,1,-1,1,\
                       -1,1,-1,1,-1,1,\
                       -1,1,-1,1)
print(result)

四维积分代码

def f(x,y,z,w):
    return x**2 + y**2 + z**2 + w**2
    


def romberg_4d(f,x1,x2,y1,y2,z1,z2,w1,w2,eps=1e-6,n=50):

    def trapezoid(f,a,b,n):
        h = (b - a) / float(n)
        s = 0.5*(f(a) + f(b))
        for i in range(1, n):
            s += f(a + i*h)
        return h*s
    
    def romberg(f,a,b,eps=1e-6,n=50):
        R = [[0]*(n+1) for i in range(n+1)]
        for i in range(1, n+1):
            h = float(b-a)/(2**i)
            R[i][1] = trapezoid(f, a, b, 2**(i-1))
            for j in range(2, i+1):
                R[i][j] = (4**(j-1)*R[i][j-1]-R[i-1][j-1])/(4**(j-1)-1)
            if abs(R[i][i]-R[i-1][i-1]) < eps:
                return R[i][i]
        raise ValueError('romberg integration failed to converge')

    def integrand_w(x,y,z):
        return romberg(lambda w:f(x,y,z,w),w1,w2,eps,n)
    def integrand_z(x,y):
        return romberg(lambda z:integrand_w(x,y,z),z1,z2,eps,n)
    def integrand_y(x):
        return romberg(lambda y:integrand_z(x,y),y1,y2,eps,n)


    return romberg(lambda x:integrand_y(x),x1,x2,eps,n)


result = romberg_4d(f,-1,1,-1,1,-1,1,-1,1)
print(result)

result

============= RESTART: 四重Romberg.py =============
21.333333333333332
>>>

Romberg数值积分原理

微积分基本定理(Newton Leibniz)
机械求积法
插值型求积
梯形公式
等距节点的N-C公式
辛普森公式
复合求积公式
高斯求积公式

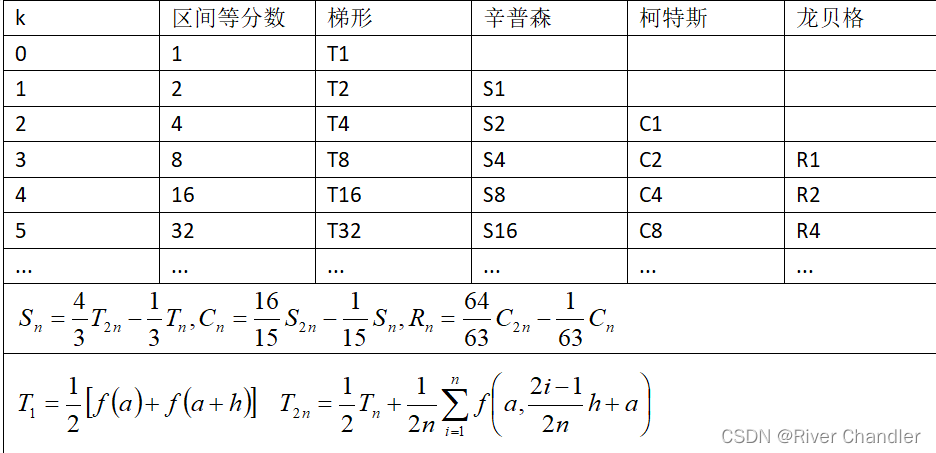
哈哈，刚才列出来的，全部不用记住，因为根本记不下来，考试前背一下就ok，至于工作的时候，你不会查手册吗？？？？

蒙特卡洛模拟替代

蒙特卡洛方法的优势在于它具有很强的适应性和灵活性，能够用于求解一些非常复杂的问题。与其他数值计算方法相比，蒙特卡洛方法不需要求解解析解，因此能够处理一些难以求解的问题，并且不会受到算法复杂度的限制。此外，蒙特卡洛方法可以直接利用随机抽样技术来求解问题，因此具有很好的并行计算能力，能够利用大规模计算资源来加速计算。
很好，那我们举一个例子吧
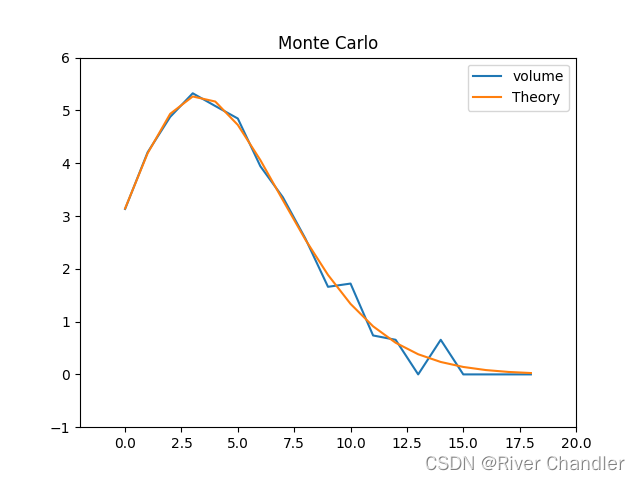
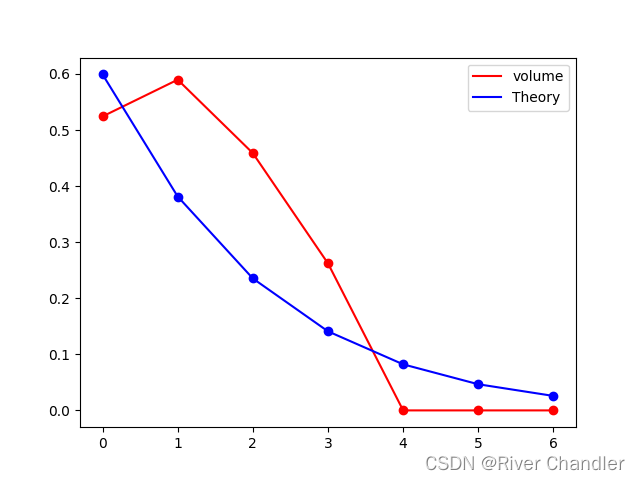
计算高维空间中球的体积：

import numpy as np
import scipy.special as spi
import matplotlib.pyplot as plt
np.random.seed(0)
import time


def prod(n):
    p = 1
    for i in range(1,n+1):
        p *= i
    return p

def f(n):
    if n%2==0:
        k = int(n/2)
        return np.pi**(k)/prod(k)
    elif n%2==1:
        k = int((n-1)/2)
        return np.pi**k*prod(k)*2**n/prod(n)

def main(Num=1e5,dim=4):
    assert(dim>=2),"dim should greater than 2!!!"
    Sum = 0
    #start = time.time()
    for i in range(int(Num)): 
        x = np.random.random(dim)
        p = sum(x**2)
        if p<=1:
            Sum += 1
    #end = time.time()
    #print("Used:",end-start)
    #print("Volume:",Sum/Num*(2**dim))
    #print("Theory:",f(dim))
    return Sum/Num*(2**dim),f(dim)

Dim = [2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20]
V = [0 for i in range(len(Dim))]
F = [0 for i in range(len(Dim))]

for i in range(len(Dim)):
    V[i],F[i] = main(dim=Dim[i])
plt.scatter(range(len(Dim)),V,c="red")
plt.scatter(range(len(Dim)),F,c="blue")
plt.plot(range(len(Dim)),V,c="red",label="volume")
plt.plot(range(len(Dim)),F,c="blue",label="Theory")
plt.legend()
plt.pause(0.01)

显然这个精度可能不太够，因此我们需要提高抽样的数量至1e6
- 事实上，依然是不够的，你的笔记本性能，数学能力，编程能力是一个不可能三角（针对有限的大学课程而言）

梯形法：四重积分为例

蒙特卡洛方法可能不能满足许多数学推导爱好者的想法，那我们用梯形法实现一下

import numpy as np

def f(x1, x2, x3, x4):
    return x1+x2+x3+x4
    
def trapezoid_integration(f, a1, b1, a2, b2, a3, b3, a4, b4, n1, n2, n3, n4):
    h1 = (b1 - a1) / n1
    h2 = (b2 - a2) / n2
    h3 = (b3 - a3) / n3
    h4 = (b4 - a4) / n4

    x1 = np.linspace(a1, b1, n1+1)
    x2 = np.linspace(a2, b2, n2+1)
    x3 = np.linspace(a3, b3, n3+1)
    x4 = np.linspace(a4, b4, n4+1)

    integral = 0
    for i in range(n1):
        for j in range(n2):
            for k in range(n3):
                for l in range(n4):
                    integral += (f(x1[i], x2[j], x3[k], x4[l]) + f(x1[i+1], x2[j], x3[k], x4[l]) +
                                f(x1[i], x2[j+1], x3[k], x4[l]) + f(x1[i+1], x2[j+1], x3[k], x4[l]) +
                                f(x1[i], x2[j], x3[k+1], x4[l]) + f(x1[i+1], x2[j], x3[k+1], x4[l]) +
                                f(x1[i], x2[j+1], x3[k+1], x4[l]) + f(x1[i+1], x2[j+1], x3[k+1], x4[l]) +
                                f(x1[i], x2[j], x3[k], x4[l+1]) + f(x1[i+1], x2[j], x3[k], x4[l+1]) +
                                f(x1[i], x2[j+1], x3[k], x4[l+1]) + f(x1[i+1], x2[j+1], x3[k], x4[l+1]) +
                                f(x1[i], x2[j], x3[k+1], x4[l+1]) + f(x1[i+1], x2[j], x3[k+1], x4[l+1]) +
                                f(x1[i], x2[j+1], x3[k+1], x4[l+1]) + f(x1[i+1], x2[j+1], x3[k+1], x4[l+1])) / 16 * h1 * h2 * h3 * h4

    return integral

a1, b1, n1 = 0, 1, 10
a2, b2, n2 = 0, 1, 10
a3, b3, n3 = 0, 1, 10
a4, b4, n4 = 0, 1, 10
integral = trapezoid_integration(f, a1, b1, a2, b2, a3, b3, a4, b4, n1, n2, n3, n4)

print("INTEGER:", integral)

INTEGER: 2.0000000000000275

现代方法

不用想，计算软件不可能这么处理高维积分
- 数值分析这么多年不可能没有发展出点别的神话操作
- 抽象代数也不是白学的
列出一些参考文献
- 徐利治，周蕴时.高维数值积分 [M]. 北京:科学出版社， 1980
- 柯召，孙琦.数论讲义 [M]. 北京:高等教育出版社， 200 1.
- 吕涛，石济民，林振宝.分裂外推与组合技巧 [M]. 北京:科学出版社， 1988.