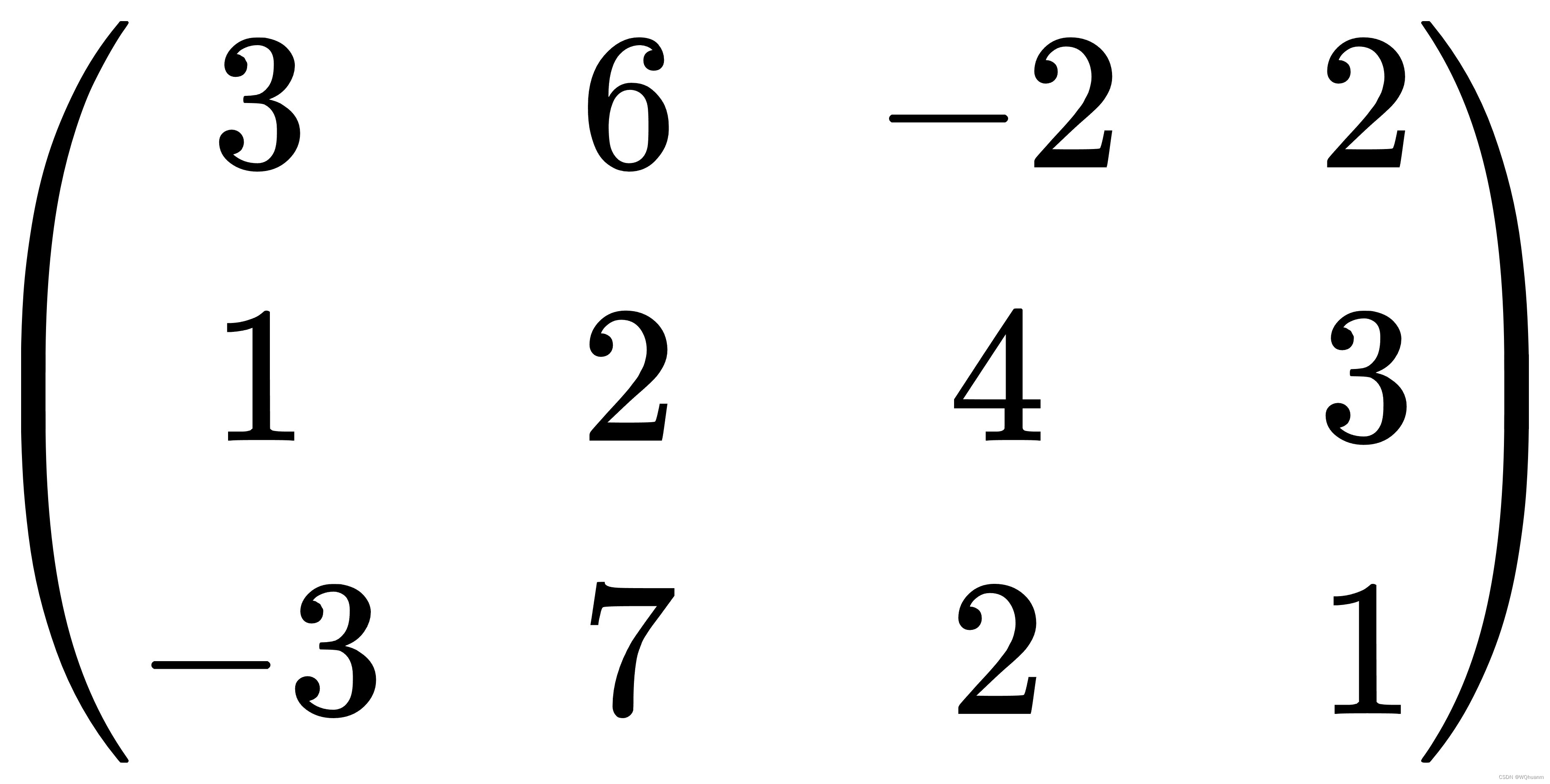1，思想

1. 该算法基于高斯消元，但是思想是把矩阵化为对角阵，从而避免回代的操作
2. 思路是一列一列处理，每次选为处理过的行中主元最大（极大避免精度损失)的行处理。把这一列除了主元这一行的元素，其余该列的其他行都化为0，最终得出对角阵
3. 举例：如下图增广矩阵

    处理第一列，我们找到主元最大的一行(即第一行），其余行该列化为0，得到

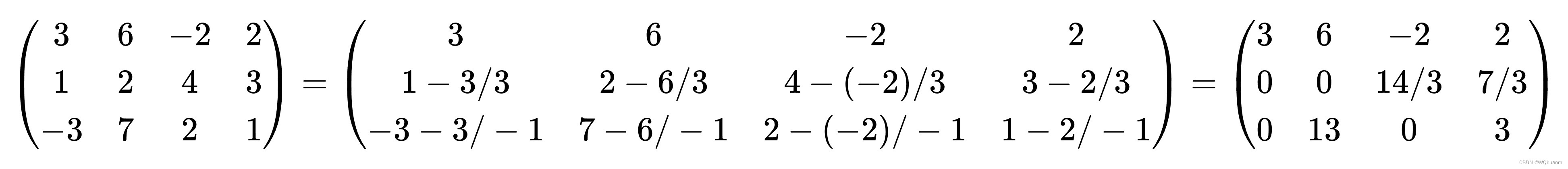
    处理第2列，我们在剩余未处理的下面两行找到主元最大的一行(即第3行，主元13），消去得：

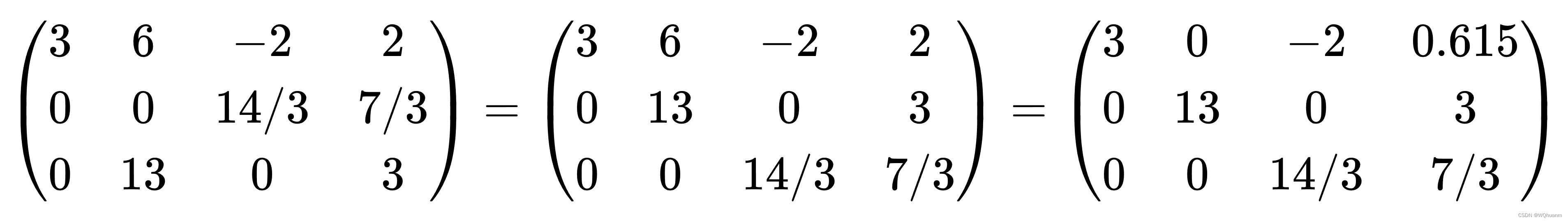
    处理最后一列，得

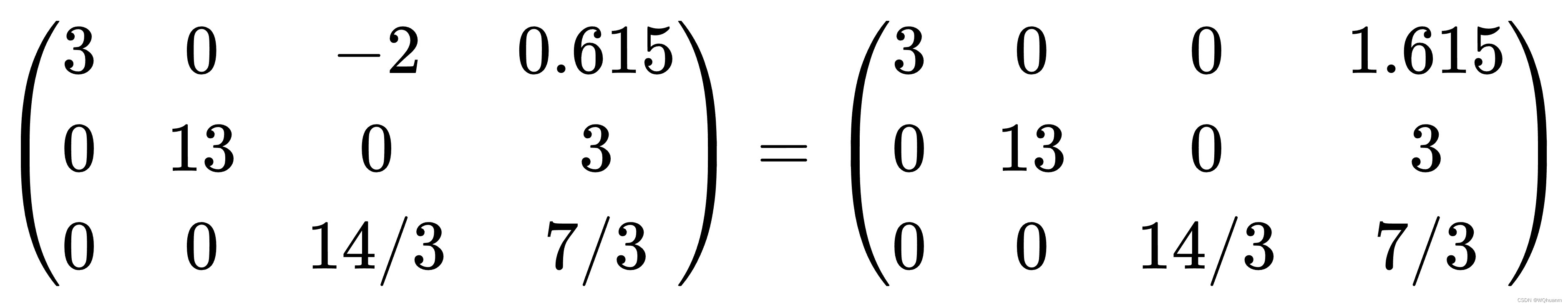
    得出对角阵，那么答案就是x1=0.54，x2=0.23，x3=0.50

   1. 

4. 那么如何处理无解与无穷解呢？

   1. 首先，他们的情况都是，ax=b中，a=0

   2. 那么如果b！=0，说明无解，其余情况就是无穷解

   3. 所以我们只需要消元后判断非0行是否为n，不是，则对0行遍历，询问这些0行是否存在b！=0，存在就是无解，不存在就是无穷解

模板：P2455 [SDOI2006]线性方程组

#include <bits/stdc++.h>
using namespace std;
#define ll               long long
#define endl             "\n"
const double eps=1e-9;
const int N = 110;
int n;
double a[N][N];

void print()//打印看目前情况
{
	cout<<endl;
	for(int i=1; i<=n; ++i)for(int j=1; j<=n+1; ++j)cout<<a[i][j]<<" \n"[j==n+1];
	cout<<endl;
}

void gauss()
{
	int r=1;//r表示目前处理到第r行
	for(int i=1; i<=n; ++i)
		{
			int mx=r;
			for(int j=r+1; j<=n; ++j)if(fabs(a[j][i]>fabs(a[mx][i])))mx=j;//第r次处理，但是比较的还是目前第i列元素（前面有可能有的列不用处理）
			if(fabs(a[mx][i])<eps)continue;//最大主元为0，当前列都为0，不用处理
			if(mx!=r)for(int j=1; j<=n+1; ++j)swap(a[r][j],a[mx][j]);//把主元最大的行提到第r行来处理
			for(int j=1; j<=n; ++j)if(j!=r)//处理不是第r行的其他行
					{
						double tmp=a[j][i]/a[r][i];
						for(int k=r; k<=n+1; ++k)a[j][k]-=a[r][k]*tmp;
					}
			r++;
			//	print();
		}
	if(r<=n)//存在0行
		{
			for(int i=r; i<=n; ++i)if(fabs(a[i][n+1])>eps)
					{
						cout<<-1<<endl;//0行但是b！=0
						return;
					}
			cout<<0<<endl;//无穷解
		}
	else for(int i=1; i<=n; ++i)printf("x%d=%.2lf\n",i,fabs(a[i][n+1]/a[i][i])<eps?0.00:a[i][n+1]/a[i][i]);//防止-0,00出现

}
void mysolve()
{
	cin>>n;
	for(int i=1; i<=n; ++i)for(int j=1; j<=n+1; ++j)cin>>a[i][j];
	gauss();
}

int32_t main()
{
	mysolve();
	system("pause");
	return 0;
}