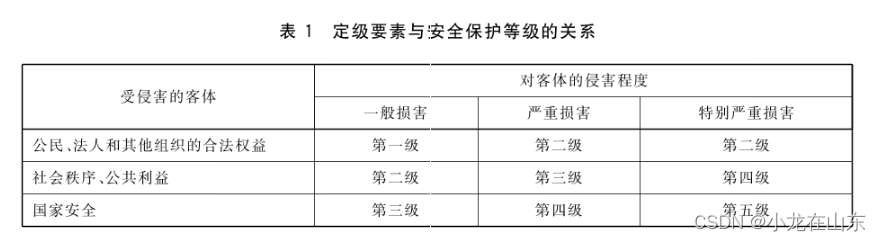
一、自相关系数:
衡量的是同一个时间序列内的两个不同的时间段的相关性
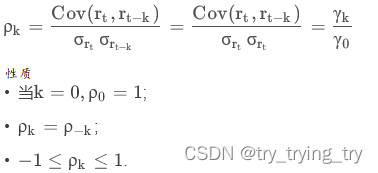
弱平稳
If波动,波动幅度也是固定的。
相关图
不同时间间隔的相关系数算出来并且绘制在图中
例:(python)
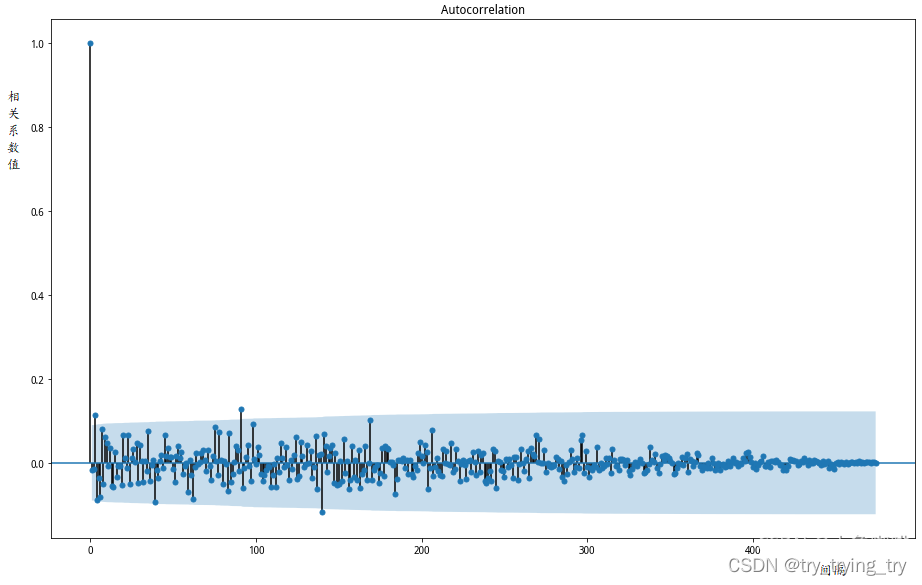
分析:
①当时间间隔为0的时候,相关系数为1,很显然,每个点和自己都是完全相关的。当时间间隔大于1,相关系数便只是在0附近波动,说明不同时间点的单日收益相关性不大。
②图中浅蓝色区域是95%的置信区间,如果相关系数在置信区间内,我们可以认为这个间隔下的子序列是不相关的。图中有个别间隔的序列相关系数超过置信区间,说明子序列还不是完全不相关的。不过大致上,我们可以认为沪深300的单日收益和其它交易日关联度不大。
二、平稳性检验:
①相关图 - 粗略判断序列是否平稳
②单位根检验 - 检验是否存在某个根大于等于1。经典是ADF检验。
ADF检验,Augmented Dickey-Fuller test
Dickey-Fuller(DF)检验的扩展。
DF检验只能应用于一阶AR模型的情况。当序列为高阶时,存在滞后相关性,于是可以使用更适用的ADF检验。
基于统计中的假设检验方式,利用t-检验来观测显著性。
注意:
当采用ADF进行检验的时候,我们实际上已经假设用AR模型对序列进行建模了。
ACF和PACF
ACF:描述了该序列的当前值与其过去的值之间的相关程度。时间序列可以包含趋势,季节性,周期性和残差等成分。
描述了一个观测值和另一个观测值之间的自相关,包括直接和间接的相关性信息。
[-1,1]
PACF:找到残差(在去除了之前的滞后已经解释的影响之后仍然存在)与下一个滞后值的相关性。

AR和MA
Auto regressive (AR) process
当前的观测值可以通过历史观测值获得
Moving average(MA) Process
当前值是由过去误差的线性组合组成的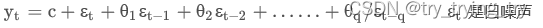
附录:
统计知识
1.
总体协方差
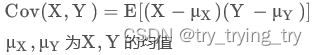
样本协方差
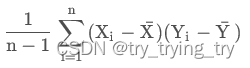
总体相关系数
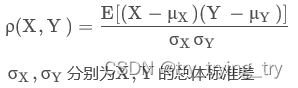
样本相关系数
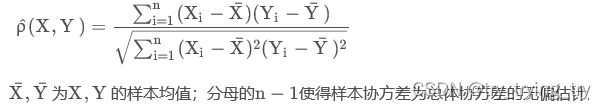
注意:

2. 时间序列

注意:
每一个时间点上是一个随机变量,有自己的分布。
时间轴上的曲线图,是给定时间段以及每个时间点的随机变量得到一个观测值后的数值序列。这个数值序列是千万种可能中的一种而已。
参考ref:
[1]平稳性、自相关性
[2]平稳性检验
[3]序列相关性-ACF,PACF和CCF 好
[4]理解ACF 和PACF