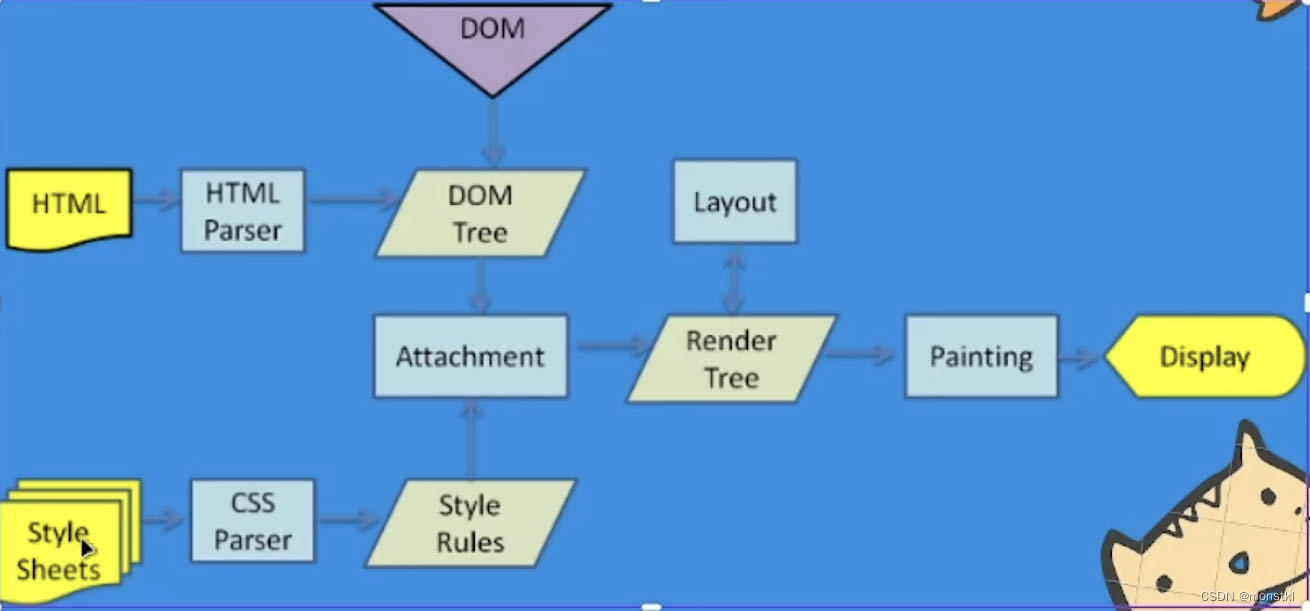
一、变换矩阵中的旋转部分

• 当我们旋转Q角度和旋转-Q角度时，变换矩阵中旋转的部分如下图所示：
  

• 旋转Q和旋转-Q的变换矩阵应该互为逆矩阵，而我们可以看到它们互为对方矩阵的转置。其实Rq是一个正交矩阵，因此其逆矩阵就是它自己的转置。当我们旋转图形一个角度为Q时，如果我们想旋转为-Q，可以直接将其变换矩阵中旋转的部分做转置。

• 3D空间中的变换：
  

• 3D空间中绕不同轴旋转的变换矩阵(y的sin是反的是因为z叉乘x才能得到y，而不是x叉乘z)：
  

二、3D空间中的旋转

• 欧拉角：
  

• 在3D空间中绕任意一条过原点的轴n旋转：
  

• 如果轴不过原点，那么我们就将它平移到原点上，再进行旋转，然后旋转完再平移回去。

• A旋转对应的旋转矩阵为MA，B旋转对应的旋转矩阵为MB，（MA+BM）/ 2 旋转矩阵对应的旋转可不是 (A+B) / 2，因此欧拉角使用欧拉角有很多不方便的地方，诸如不能还原角度、万向节死锁。建议使用四元数表示旋转。

三、Veiwing transformation

 我们变换的最终目的是把三维空间中的物体，变成一张二维的照片。我们需要做的变换为如下MVP变换：

• 模型变换：把物体摆好，把场景搭建好。
• 视图变换：把相机摆好，把相机的位置和方向确定下来。
• 投影变换：根据场景和相机，把三维空间投影到二维中。

（1）View / Camera transformation

 相机具有的属性有：

• 位置POS、方向FRONT、向上方向UP(相机转动角度垂直于向上方向)。

 以上就是观测矩阵需要的定义。

• 当相机和场景中的物体相对位置保持不变时，拍出来的照片内容相同。因此为什么我们不讲相机永远固定在一个位置呢？

• 我们定义相机永远位于原点、朝向负Z方向、向上方向为Y轴。

• 进行视图变换(将相机平移到原点，朝向-Z轴，向上为Y轴)：
  

• 平移矩阵很简单：
  

• 怎么旋转呢？将摄像机的朝向g转向-Z，将摄像机的向上方向t转向Y，而g×t自然朝向X。可是g转向-Z不好写，有什么简单的呢？我们可以简单的写出X转向g×t 和 Y转向t，这样Z自然就转向-g了，这个矩阵为：
  

• 上图中矩阵乘以(1,0,0,0)即X轴会得到(Xgt，Ygt，Zgt)即g×t的方向，乘以(0,1,0,0)即Y轴会得到(Xt，Yt，Zt)即相机向上方向t，乘以(0,0,1,0)即Z轴会得到(X-g，Y-g，Z-g)则把Z轴转向摄像机方向的反向。因此上图矩阵可以把XYZ轴分别旋转到g×t、t、-g方向。

• 现在我们需要的是把g×t、t、g方向分别旋转到XY -Z轴，那该怎么办呢？我们又知道变换矩阵中旋转部分是一个正交矩阵，只要转置就能得到逆矩阵，就能得到 “把XYZ轴分别旋转到g×t、t、-g方向” 的逆操作 “g×t、t、g方向分别旋转到XY -Z轴”。因此我们使用逆矩阵即可。
  

• 我们将物体和相机一起应用观察矩阵即可保证它们的相对位置不变，同时还把相机移到了一个规范通用简单的位置。

• 模型矩阵：怎样拜访物体。视图矩阵：怎样把物体和相机摆放到标准位置。模型矩阵和视图矩阵都会应用到物体上。

（2）Projection transformation

 当我们把相机和场景都移动到标准位置，即相机位于原点朝向-Z轴时，我们如何得到相机看到的画面呢？想象现在有一个相机，我们知道它的位置（一个点）、朝向（一个向量），我们总不能只描绘出一个点吧？类比我们人类的眼睛，其实可以看到一定角度中的内容，而透视投影定义的就是如何将三维空间投影到一个二维平面上。
 透视投影会看到平行的线不再平行，比如你的眼睛。正交投影不会带来"近大远小"的效果。两种投影的示意图如下：

 从z方向看的好处是我们可以扔掉物体的z坐标(区分前后内容后面再讨论)，只保留x和y。然后不管相机拍摄覆盖区域有多大，我们都把它们的x、y值移动到【-1,1】的区间中。

（2.1）Orthographic projection

 正交投影需要投影一个立方体区域，它假设摄像机距离场景无限远，因此摄像机镜头的边界是两束平行光。定义正交投影，就是定义这样一个立方体是什么样的，我们规定这个立方体有如下参数：

 要注意Z轴朝向的是屏幕以外，即Z值越小其位置离我们越远。不管立方体是怎么样的，我们只需要把它移动到原点然后再缩放到【-1,1】中。

 上述变换对应的变换矩阵如下：

 当我们把原本的一个立方体缩放到【-1，1】，会导致物体的拉伸，但是在所有的变换都做完，所有的物体都处在【-1，1】立方体内时，还会做一次拉伸叫做视口变换。(缩放是xyz都要缩放)
 正交投影的立方体块是我们自己定义的，想要投影哪一块就定义哪一块，设置对应的立方体块参数。

（2.2）Perspective projection

 使用最多的投影方式；近大远小；投影后平行线不再平行，如下图所示：

• 透视投影会将平面投影到另一个平面上，导致平行线不再平行。
  

• 透视投影和正交投影的示意图
  

• 透视投影：先将Frustum四面体挤成一个Cuboid立方体，再进行正交投影。Frustum近平面永远不变，远平面的z值不变，Frustum中心点不变。我们现在要做的是求变换矩阵，从透视到正交的变换矩阵。
  

• 原本的Z值不管，对于Y，从侧面分析得到以下式子：
  

• 对X同理应用相似三角形，得到：
  

• 设变换矩阵为：
  
  

• 根据近平面和远平面中心点不变推导得到参数为：