一、题目描述

给定一个排序数组和一个目标值，在数组中找到目标值，并返回其索引。如果目标值不存在于数组中，返回它将会被按顺序插入的位置。

请必须使用时间复杂度为 O(log n) 的算法。

示例 1:

输入: nums = [1,3,5,6], target = 5
输出: 2

示例 2:

输入: nums = [1,3,5,6], target = 2
输出: 1

示例 3:

输入: nums = [1,3,5,6], target = 7
输出: 4

提示:

1 <= nums.length <= 104
-104 <= nums[i] <= 104
nums 为无重复元素的升序排列数组
-104 <= target <= 104

二、题目分析&解题思路&代码实现

注意题目中所说要求：请必须使用时间复杂度为 O(log n) 的算法。且 nums 为无重复元素的升序排列数组
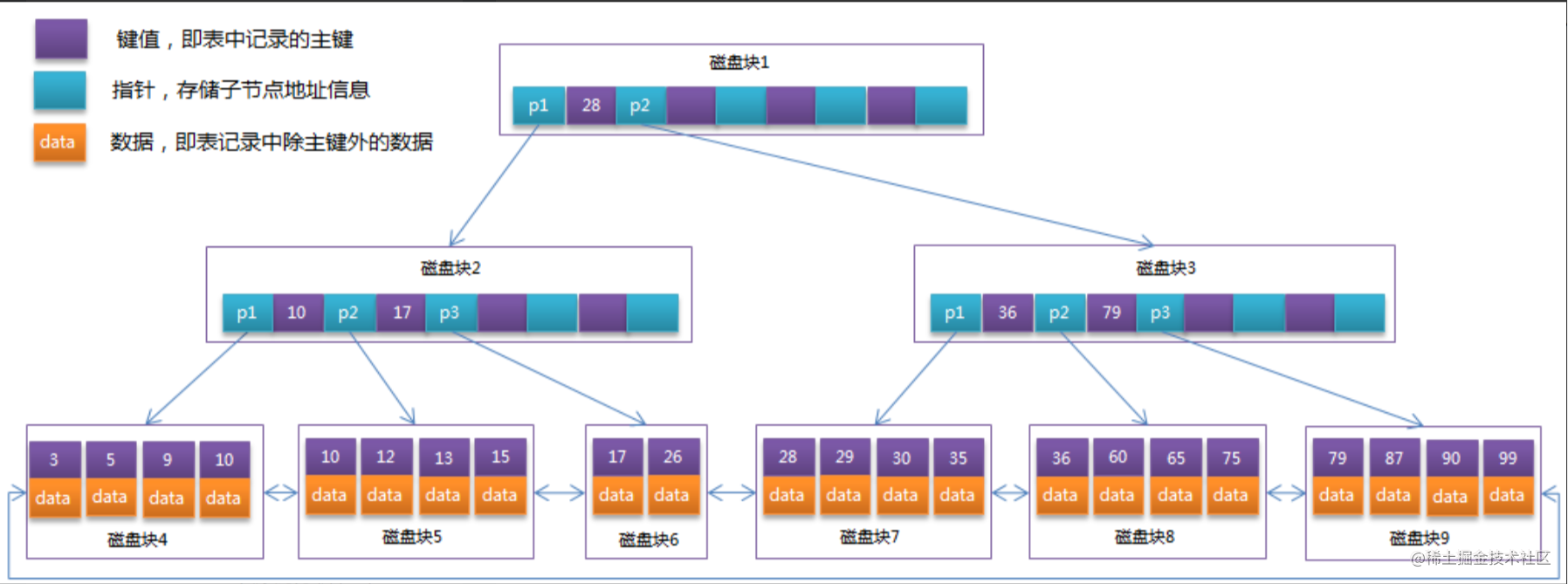
如果对二分法还不了解的可以看下面的示例：
例如我们需要查找的数字是 5
在这里插入图片描述
二分法的思想就是，既然是升序的数组，那么这个需要查找的目标数字一定在这个数组的左区间或者右区间，当然了如果是无序的话，那么二分法将没有任何意义，而我们需要做的就是不断去缩小左右区间：
示例：
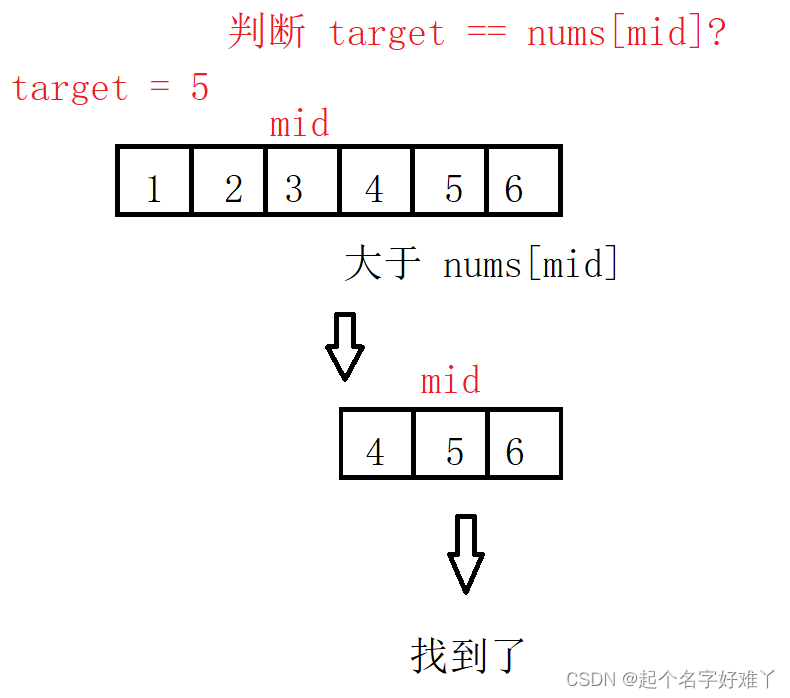
在这里插入图片描述
两次就找到了，最坏情况下 3 次也就找到了，因为 2^2 <= 6 <= 2^3 因此这是一个标准的时间复杂度为 O(log n) 的算法。
代码示例：

    int searchInsert(vector<int>& nums, int target) {
        int left = 0;
        int right = nums.size()-1;
        int iResult = nums.size();//找不到比他小的数说明在最后元素的后一个位置
        while(left <= right)
        {
            int mid = (left+right)/2;
            if(nums[mid] >= target)//目标数字在左区间
            {
                iResult = mid;
                right = mid -1;//缩小右边界
            }
            else//目标数字在区间
            {
                left = mid+1;//缩小左边界
            }

        }
        return iResult;