🎆🎉🎉🎉🎉🎉🎉🎉🎉🎉🎉🎆
今天我要开启一个新计划----【C++天梯计划】
目的是通过天梯计划，通过题目和知识点串联的方式，完成C++复习与巩固。

什么是二叉树？

二叉树（Binary tree）是树形结构的一个重要类型。许多实际问题抽象出来的数据结构往往是二叉树形式，即使是一般的树也能简单地转换为二叉树，而且二叉树的存储结构及其算法都较为简单，因此二叉树显得特别重要。二叉树特点是每个节点最多只能有两棵子树，且有左右之分 。
二叉树是n个有限元素的集合，该集合或者为空、或者由一个称为根（root）的元素及两个不相交的、被分别称为左子树和右子树的二叉树组成，是有序树。当集合为空时，称该二叉树为空二叉树。在二叉树中，一个元素也称作一个节点 。

二叉树的定义

二叉树（binary tree）是指树中节点的度不大于2的有序树，它是一种最简单且最重要的树。二叉树的递归定义为：二叉树是一棵空树，或者是一棵由一个根节点和两棵互不相交的，分别称作根的左子树和右子树组成的非空树；左子树和右子树又同样都是二叉树 。

二叉树的基本形态

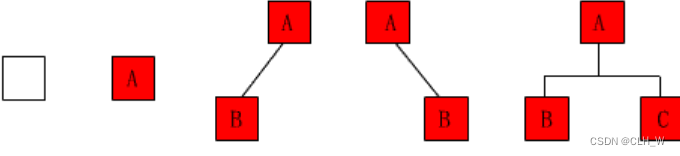
二叉树是递归定义的，其节点有左右子树之分，逻辑上二叉树有五种基本形态
1、空二叉树——如图（1）
2、只有一个根节点的二叉树——如图（2）
3、只有左子树——如图（3）
4、只有右子树——如图（4）
5、完全二叉树——如图（5）

1-----------2-----------------3---------------4------------------5

二叉树的性质

性质1： 二叉树的第i层上至多有2i-1（i≥1）个节点 [6] 。
性质2： 深度为h的二叉树中至多含有2h-1个节点 [6] 。
性质3： 若在任意一棵二叉树中，有n0个叶子节点，有n2个度为2的节点，则必有n0=n2+1 [6] 。
性质4： 具有n个节点的满二叉树深为log2n+1。
性质5： 若对一棵有n个节点的完全二叉树进行顺序编号（1≤i≤n），那么，对于编号为i（i≥1）的节点：
当i=1时，该节点为根，它无双亲节点。
当i>1时，该节点的双亲节点的编号为i/2 。
若2i≤n，则有编号为2i的左节点，否则没有左节点。
若2i+1≤n，则有编号为2i+1的右节点，否则没有右节点 。

例题1：二叉树的遍历

题目描述

给出一个 nn 个结点的二叉树，请求出二叉树的前序遍历，中序遍历和后序遍历。

输入

第一行有一个整数 nn (0 < n ≤ 260<n≤26)，表示二叉树有 nn 个结点；
以下 nn 行，每行第一个为一个大写字母表示结点的值，第 i+1i+1 行的结点编号为 ii ；
后面为两整数，第一个表示该结点左孩子结点编号，第二个表示该结点右孩子的结点编号，如果该编号为 00 表示没有；（编号为 11 的结点是树的根）

输出

共三行，第一行为二叉树的前序遍历，第二行为中序遍历，第三行为后序遍历；

样例

输入
7
F 2 3
C 4 5
E 0 6
A 0 0
D 7 0
G 0 0
B 0 0
输出
FCADBEG
ACBDFEG
ABDCGEF

代码

#include <bits/stdc++.h>
using namespace std;
//1.用孩子表示法，存储二叉树
//2.用递归的方法得到先序中序后序遍历的结果 
const int N = 30;
struct node{
	char c;
	int lc,rc;//左右孩子 
}a[N]; 
int n;

//前序遍历：根左右 
void dfs1(int x){
	cout<<a[x].c;
	if(a[x].lc) dfs1(a[x].lc);
	if(a[x].rc) dfs1(a[x].rc);
} 

//中序
void dfs2(int x){
	if(a[x].lc) dfs2(a[x].lc);
	cout<<a[x].c;
	if(a[x].rc) dfs2(a[x].rc);
}
//后序 
void dfs3(int x){
	if(a[x].lc) dfs3(a[x].lc);
	if(a[x].rc) dfs3(a[x].rc);
	cout<<a[x].c;
}

int main(){
	cin>>n;
	//读入结点
	for(int i = 1;i <= n;i++){
		cin>>a[i].c>>a[i].lc>>a[i].rc;
	} 
	
	//深搜
	//前序遍历
	dfs1(1);	
	cout<<endl;
	//中序遍历
	dfs2(1);
	cout<<endl;
	//后序遍历
	dfs3(1);
	return 0;
}

例题2：哈夫曼树

题目描述

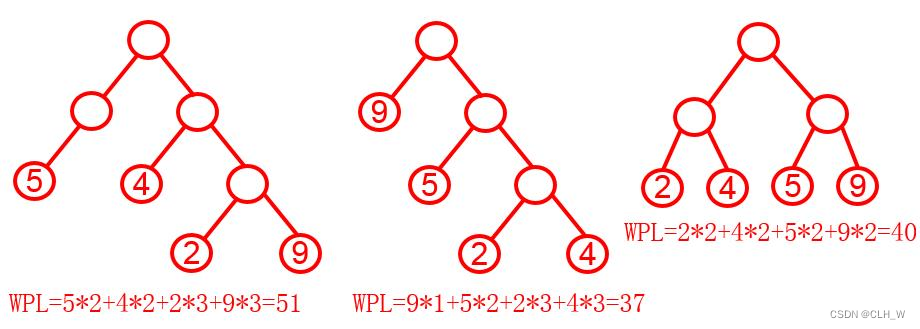
哈夫曼树的定义是：一棵具有 nn 个带权叶结点的二叉树，使得所有叶结点的带权路径长度（叶结点 ×× 叶结点到根结点的路径长度）之和最小，这样的二叉树被称为最优二叉树，也称哈夫曼树。

比如：有 44 个结点的权值是55 44 22 99，可以构建出如下三颗不同的二叉树，第 22 棵二叉树的带权路径长度是最小的。
请读入一个整数 nn ，代表叶结点的数量，再读入 nn 个整数，代表叶结点的权值，请求出对应哈夫曼树的带权路径长度。

输入

输入的第一行包含一个正整数 nn（n≤100n≤100）。
接下来是 nn 个正整数，表示 nn 个叶结点的权值，每个数不超过 10001000 。

输出

输出构造出的哈夫曼树的带权路径长度。

样例

输入
5
5 3 8 2 9
输出
59

代码

#include <bits/stdc++.h>
using namespace std;
//思路：使用优先队列模拟哈夫曼树的构建过程
//小根堆 
priority_queue<int,vector<int>,greater<int> > q; 
int n,x,ans = 0;//ans：代表哈夫曼树的WPL的值 
 
int main(){
	cin>>n;
	//读入n个元素 
	while(n--){
		cin>>x;
		q.push(x);
	}
	
	//当队列中超过1个元素
	//获取队列头部的2个最小的元素
	int a,b; 
	while(q.size() > 1){
		a = q.top();
		q.pop();
		b = q.top();
		q.pop();
		
		ans += a + b;
		q.push(a+b);
	} 
	
	cout<<ans; 
	return 0;
}