【C++进阶3-二叉搜索树】强，但没貌似还不够？

news2024/11/27 22:35:29

今天，带来二叉搜索树的讲解。

文中不足错漏之处望请斧正！

是什么

二叉搜索树（Binary Search Tree）又称二叉排序树。

它可以是一棵空树，也可以是具有以下性质的二叉树:

  • 若它的左子树不为空，则左子树上所有结点的值都小于根结点的值
  • 若它的右子树不为空，则右子树上所有结点的值都大于根结点的值
  • 它的左右子树也分别为二叉搜索树

实现

二叉搜索树有两种搜索模型——Key搜索模型和<Key, Value>搜索模型。

Key搜索模型

Key模型的BST每个结点内存一个Key值，即用Key作为关键码，Key本身就是搜索需要找到的值。

结构

template<class K>
struct BSTreeNode
{
    BSTreeNode(const K& key)
    :_left(nullptr),
    _right(nullptr),
    _key(key)
    {}
    
    BSTreeNode<K>* _left = nullptr;
    BSTreeNode<K>* _right = nullptr;
    K _key;
};

template<class K>
class BSTree
{
    typedef BSTreeNode<K> Node;
public:
		Node* _root = nullptr;
};

Insert

思路：key小往左走，key大往右走。

参考代码

		//依照key值找插入位置（BST元素不重复）
    bool Insert(const K& key)
    {
        if(_root == nullptr)
        {
            _root = new Node(key);
            return true;
        }
        
        Node* cur = _root, *parent = nullptr;
        while(cur)
        {
            if(cur->_key < key)
            {
                parent = cur;
                cur = cur->_right;
            }
            else if(key < cur->_key)
            {
                parent = cur;
                cur = cur->_left;
            }
            else
                return false;
        }
        
        cur = new Node(key);
        if(parent->_key < key)
            parent->_right = cur;
        else
            parent->_left = cur;
        
        return true;
    }

Erase

思路：

1. 要删的是根/没有孩子的结点

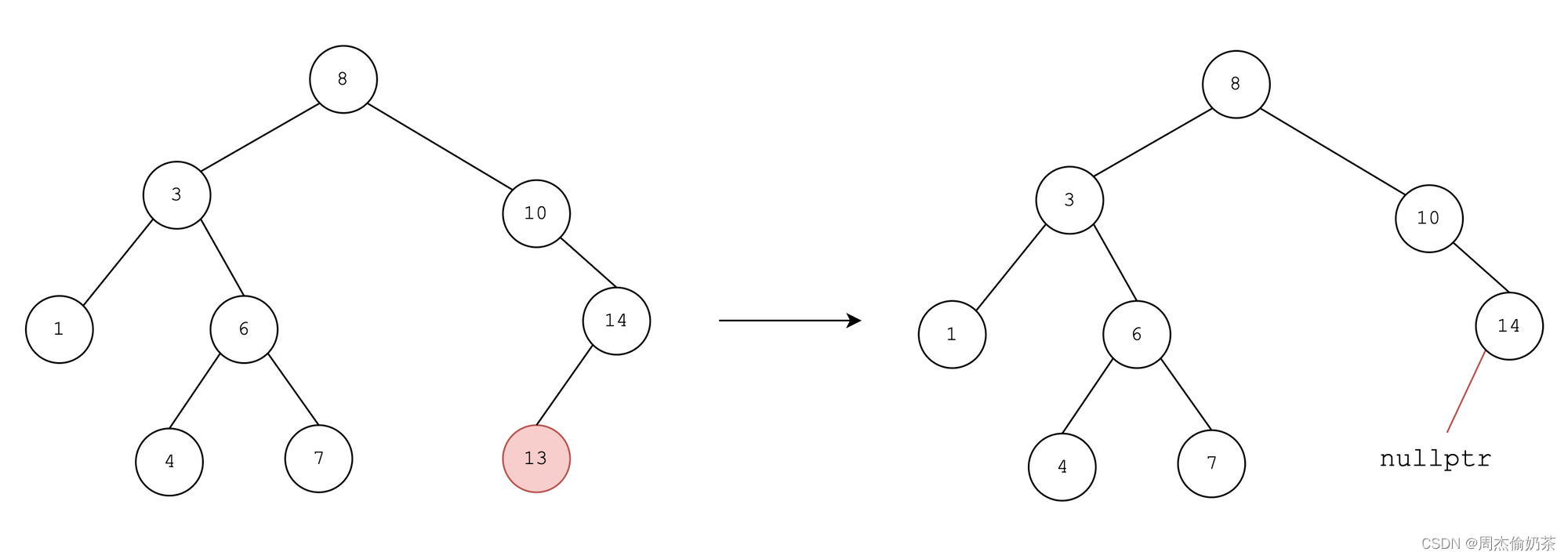
在这里插入图片描述

：直接删

2. 要删的有左孩子/右孩子

在这里插入图片描述

：将左/右孩子托付给自己的父。

3. 要删的有左右孩子

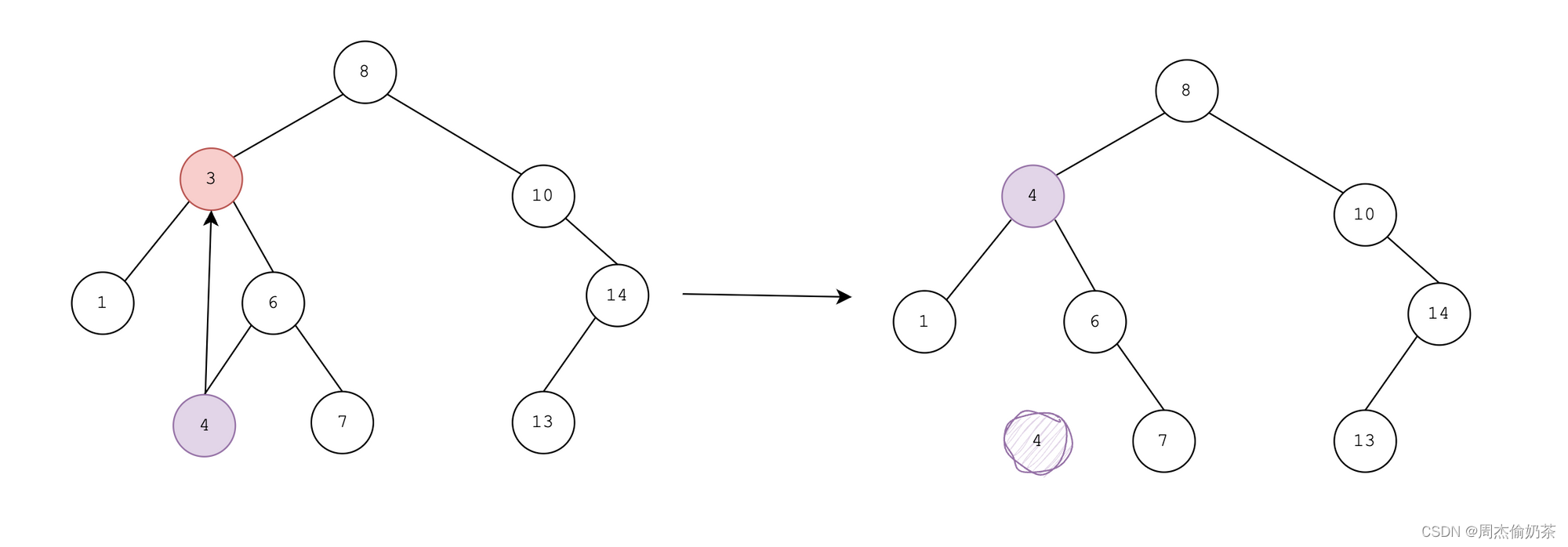
在这里插入图片描述

在这里插入图片描述

替换法删除：找一个合适的结点替换删除。

找谁？

左子树最大 / 右子树最小都可以。

  • BST规则：左子树的全部结点都比右子树小，也可以说右子树的全部结点都比左子树的大。
  • 左子树最大的上来作根：比左子树的都大，比右子树的都小（）
  • 右子树最小的上来作根：比右子树的都小，比左子树的都大（BST规则：左子树的全部都比右子树小）

参考代码

		bool Erase(const K& key) //删除 = 删除 + 链接
    {
        if(Empty()) return false;
        
        Node* cur = _root, *parent = nullptr;
        while(cur)
        {
            if(cur->_key < key)
            {
                parent = cur;
                cur = cur->_right;
            }
            else if(key < cur->_key)
            {
                parent = cur;
                cur = cur->_left;
            }
            else break;
        }
        
        if(cur == nullptr) return false;
        
        //走到这，cur即要删除的结点
        
        //要删的是根 / 要删的结点没有孩子都可以直接包含在这种条件内（复用代码）
        //2. 要删的结点有右孩子 ==> 将右子树托孤
        if(cur->_left == nullptr)
        {
            if(cur == _root)
            {
                _root = cur->_right;
            }
            else
            {
                if(cur == parent->_left)
                    parent->_left = cur->_right;
                else
                    parent->_right = cur->_right;
            }
            delete cur;
            return true;
        }
        //2. 要删的结点有左孩子 ==> 将左子树托孤
        else if(cur->_right == nullptr)
        {
            if(cur == _root)
            {
                _root = cur->_left;
            }
            else
            {
                if(cur == parent->_left)
                    parent->_left = cur->_left;
                else
                    parent->_right = cur->_left;
            }
            delete cur;
            return true;
        }
        //3. 要删的结点有左右孩子 ==> 替换法删除
        else
        {
            Node* minRight = cur->_right, *parent = cur;
            while(minRight->_left) //此分支内，minRight肯定不为空，可以直接解引用
            {
                parent = minRight;
                minRight = minRight->_left;
            }
            
						//覆盖掉要删的
            cur->_key = minRight->_key; 
            if(minRight == parent->_left)
                parent->_left = minRight->_right;
            else
                parent->_right = minRight->_right;
            //我已经去作老大了，这里得清理干净
            delete minRight;
            return true;
        }
        
        return false;
    }

InsertR

可以用递归实现一下，有个很妙的点。

我们插入和删除最大的难点就是链父，插入了，我的父是谁，删除了，我的父是谁？

在递归里，这样的场景我们可以用引用做参数——使得root是父亲的左/右孩子的引用。

		bool _InsertR(Node*& root, const K& key)
    {
        //最大的问题是链父，root作引用，是父结点的left/right
        if(root == nullptr)
        {
            root = new Node(key); //root是父结点的left/right的引用，这一步赋值相当于链父了
            return true;
        }
        
        if(root->_key < key)
            return _InsertR(root->_right, key);
        else if(key < root->_key)
            return _InsertR(root->_left, key);
        else
            return false;
    }

EraseR

递归里我们不能用替换法直接覆盖删了，但是思路一样，还是需要替换，不过绕了个弯子。

我们可以替换，让左子树最大/右子树最小，也可以说是最左/最右结点作根，原本的根换下去。

有两个点：

  1. 最左结点/最右结点必然有一侧是空的，那就可以直接删除或托孤
  2. 替换后不符合BST规则：整体来说不符合，但是从局部来说还符合

局部符合有什么用？
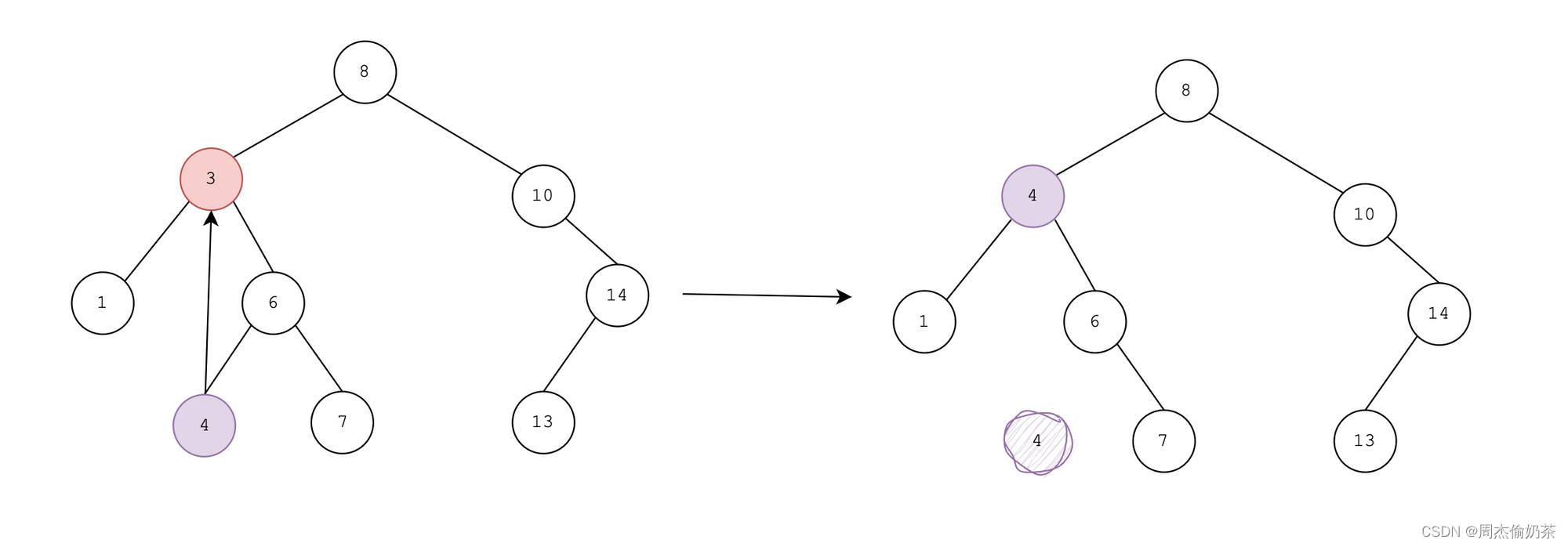
在这里插入图片描述

局部符合我们就可以在局部删！

	bool _EraseR(Node*& root, const K& key)
    {
        if(root == nullptr) return false;
        
        if(root->_key < key)
            return _EraseR(root->_right, key);
        else if(key < root->_key)
            return _EraseR(root->_left, key);
        else
        {
            Node* del = root;
            
            if(root->_left == nullptr)
                root = root->_right; //托孤（右孩子）
            else if(root->_right == nullptr)
                root = root->_left; //托孤（右孩子）
            else
            {
                Node* minRight = root->_right;
                while(minRight->_left)
                    minRight = minRight->_left;
                //交换法：直接找key删，没法删，找替换节点交换，交换后可以删替换节点
                //(因为是最左/最右结点，一定有一侧是空的，也就可以托孤)
                swap(root->_key, minRight->_key);
                //交换后，root为根的子树不符合BST，无法递归，会找不到key
                //但是，因为找来的替换节点是右子树的最左节点，替换后右子树保持BST
                //就可以转换成到root->_right为根的子树找，而交换后，我们可以用托孤的方式删除minRight/maxLeft
                _EraseR(root->_right, key);
            }
            
            delete del;
            
            return true;
        }
    }

子函数

我们把这些需要传递私有成员的函数都作为子函数，或是弄一层函数重载——外面调用时是无法访问私有成员，所以无法传参。

*其实可以写一个GetRoot这种函数给外面提供，但是暴露底层了，不好

子函数：

		//外面可以直接调用
		void InOrder()
		{
			 _InOrder(_root); 
		}
		//封一层
		void _InOrder(Node* root)
    { ... }

函数重载：

		//给外面调用
		void InOrder()
		{
			 InOrder(_root); 
		}
		//给内部调用
		void _InOrder(Node* root)
    { ... }

还有一些拷贝构造和析构什么的，完善一下就好了。

*整体代码在文末

<Key, Value>搜索模型

KV模型的BST每个结点内存一个pair键值对，即用pair中的Key作为关键码，Key对应的Value是需要找到的值。

关于键值对，它存放了一个键和相应值的对，键用于在树中进行查找，而值则相当于查找键所得到的结果。

C++中的pair类模板是一种将两个值组合成一个单元的数据结构。这对于需要将一对值作为一个单元处理的情况非常有用。pair模板具有两个模板参数，一个表示第一个值的类型，另一个表示第二个值的类型。例如，pair<int, string>是一个由int和string类型组成的单元。我们此处用它来将key和value组合成一个单元，实现KV搜索模型。

实现

实现上我们从简，只玩儿精华，看到它和K模型的区别即可。

//KV查找模型：key value
namespace KV
{
template<class K, class V>
struct BSTreeNode
{
    BSTreeNode<K, V>* _left = nullptr;
    BSTreeNode<K, V>* _right = nullptr;
    K _key;
    V _val;
    
    BSTreeNode(const K& key, const V& val)
    :_left(nullptr),
    _right(nullptr),
    _key(key),
    _val(val)
    {}
};

template<class K, class V>
class BSTree
{
public:
    typedef BSTreeNode<K, V> Node;
    
    BSTree()
    :_root(nullptr)
    {}

    bool Insert(const K& key, const V& val)
    {
        if(_root == nullptr)
        {
            _root = new Node(key, val);
            return true;
        }
        
        Node* cur = _root, *parent = nullptr;
        while(cur)
        {
            if(cur->_key < key)
            {
                parent = cur;
                cur = cur->_right;
            }
            else if(key < cur->_key)
            {
                parent = cur;
                cur = cur->_left;
            }
            else
                return false;
        }
        
        cur = new Node(key, val);
        if(parent->_key < key)
            parent->_right = cur;
        else
            parent->_left = cur;
        
        return true;
    }
    
    void InOrder()
    {
        _InOrder(_root); //递归必须要传root：子函数内部传参，不想写GetRoot暴露root
        cout << endl;
    }
    
    Node* Find(const K& key)
    {
        Node* cur = _root;
        while(cur)
        {
            if(cur->_key == key)
                return cur;
            else if(cur->_key < key)
                cur = cur->_right;
            else
                cur = cur->_left;
        }
        return nullptr;
    }

    void _InOrder(Node* root)
    {
        if(root == nullptr) return;
        
        _InOrder(root->_left);
        
        cout << "["
                << root->_key
                << ", "
                << root->_val
            << "]" << endl;
        
        _InOrder(root->_right);
    }
private:
    
    Node* _root = nullptr;
};

BST性能分析

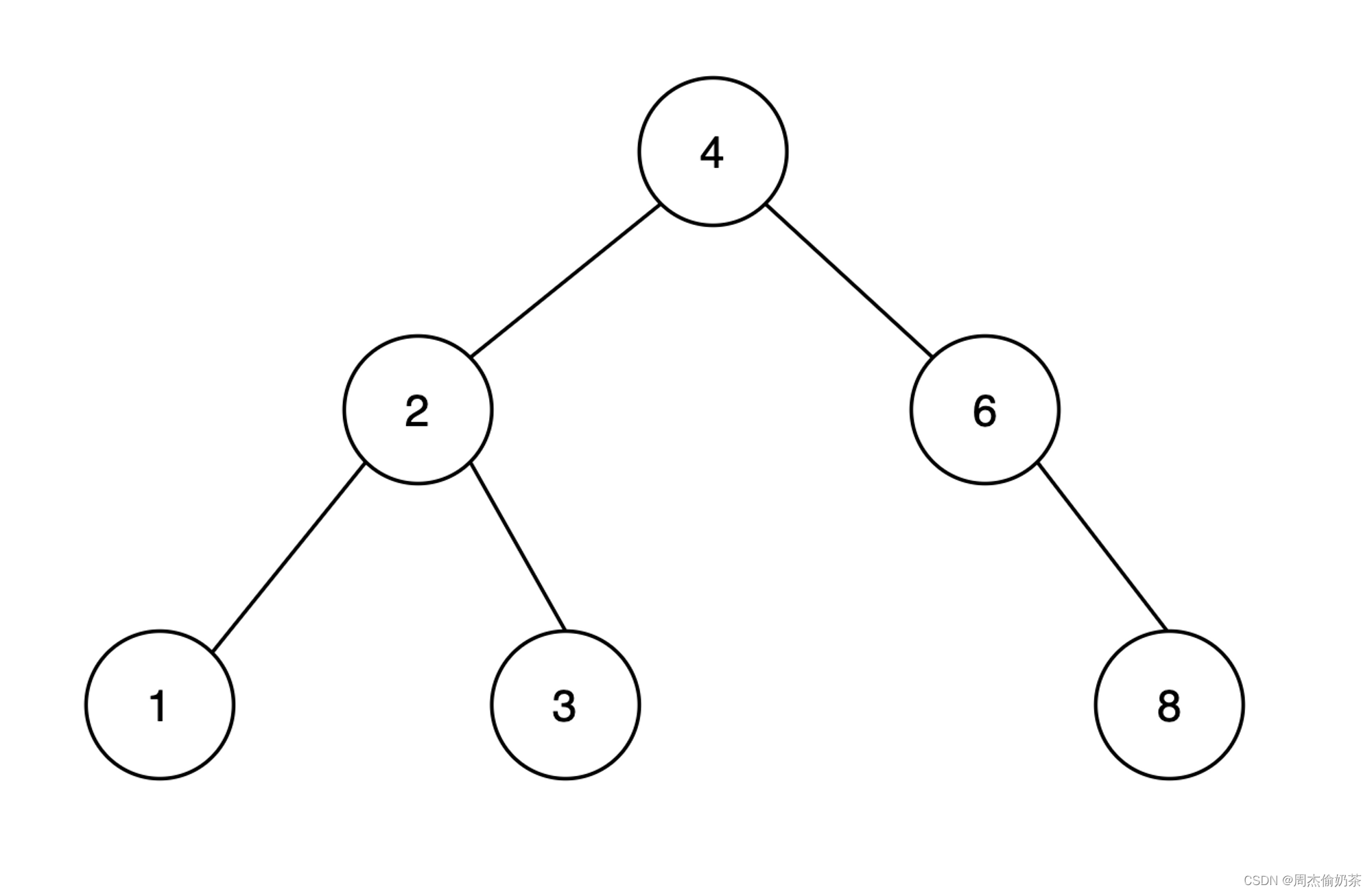
最优情况

是或接近完全二叉树，据key搜索一次需要比较logN次，时间复杂度为O(N)。

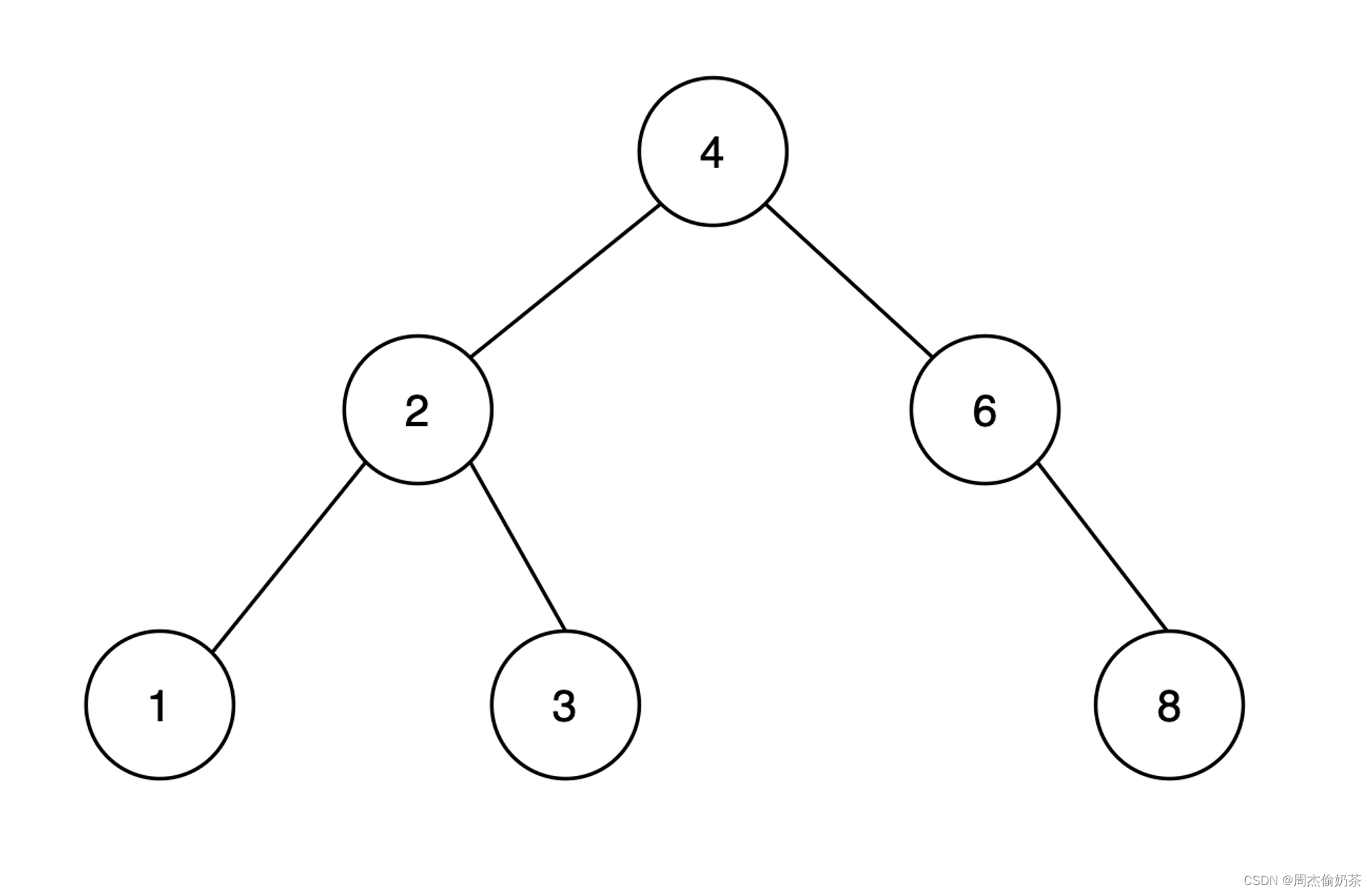
在这里插入图片描述
还是很不错的哦！

最差情况

是或接近单支树，据key搜索一次需要比较N次，时间复杂度为O(N)。

在这里插入图片描述
但是会退化，感觉不够强……

K模型BST的整体参考代码

整体参考代码

//Key搜索模型
template<class K>
struct BSTreeNode
{
    BSTreeNode(const K& key)
    :_left(nullptr),
    _right(nullptr),
    _key(key)
    {}
    
    BSTreeNode<K>* _left = nullptr;
    BSTreeNode<K>* _right = nullptr;
    K _key;
};

template<class K>
class BSTree
{
    typedef BSTreeNode<K> Node;
public:
    BSTree()
    :_root(nullptr)
    {}
    
    ~BSTree()
    {
        Destroy(_root);
    }
    
    BSTree(const BSTree<K>& t)
    {
        _root = Copy(t._root);
    }
    
    BSTree<K>& operator=(BSTree<K> t)
    {
        swap(_root, t._root);
        return *this;
    }
    
    //依照key值找插入位置（BST元素不重复）
    bool Insert(const K& key)
    {
        if(_root == nullptr)
        {
            _root = new Node(key);
            return true;
        }
        
        Node* cur = _root, *parent = nullptr;
        while(cur)
        {
            if(cur->_key < key)
            {
                parent = cur;
                cur = cur->_right;
            }
            else if(key < cur->_key)
            {
                parent = cur;
                cur = cur->_left;
            }
            else
                return false;
        }
        
        cur = new Node(key);
        if(parent->_key < key)
            parent->_right = cur;
        else
            parent->_left = cur;
        
        return true;
    }
    
    void InOrder()
    {
        _InOrder(_root); //递归必须要传root：子函数内部传参，不想写GetRoot暴露root
        cout << endl;
    }
    
    bool Find(const K& key)
    {
        Node* cur = _root;
        while(cur)
        {
            if(cur->_key == key)
                return true;
            else if(cur->_key < key)
                cur = cur->_right;
            else
                cur = cur->_left;
        }
        return false;
    }
    
    bool Empty() { return _root == nullptr;}
    
    bool Erase(const K& key) //删除 = 删除 + 链接
    {
        if(Empty()) return false;
        
        Node* cur = _root, *parent = nullptr;
        while(cur)
        {
            if(cur->_key < key)
            {
                parent = cur;
                cur = cur->_right;
            }
            else if(key < cur->_key)
            {
                parent = cur;
                cur = cur->_left;
            }
            else break;
        }
        
        if(cur == nullptr) return false;

        if(cur->_left == nullptr)
        {
            if(cur == _root)
            {
                _root = cur->_right;
            }
            else
            {
                if(cur == parent->_left)
                    parent->_left = cur->_right;
                else
                    parent->_right = cur->_right;
            }
            delete cur;
            return true;
        }
        else if(cur->_right == nullptr)
        {
            if(cur == _root)
            {
                _root = cur->_left;
            }
            else
            {
                if(cur == parent->_left)
                    parent->_left = cur->_left;
                else
                    parent->_right = cur->_left;
            }
            delete cur;
            return true;
        }
        else
        {
            Node* minRight = cur->_right, *parent = cur;
            while(minRight->_left) //此分支内，minRight肯定不为空
            {
                parent = minRight;
                minRight = minRight->_left;
            }
            
            cur->_key = minRight->_key; //左子树最大 / 右子树最小都符合
            if(minRight == parent->_left)
                parent->_left = minRight->_right;
            else
                parent->_right = minRight->_right;
            
            delete minRight;
            return true;
        }
        
        return false;
    }
    

    
    bool InsertR(const K& key)
    {
        return _InsertR(_root, key);
    }
    
    bool EraseR(const K& key)
    {
        return _EraseR(_root, key);
    }

    bool FindR(const K& key)
    {
        return _FindR(_root, key);
    }

private:
    void Destroy(Node* root)
    {
        if(root == nullptr) return;
        
        Destroy(root->_left);
        Destroy(root->_right);
        
        delete root;
    }
    
    Node* Copy(Node* root)
    {
        if(root == nullptr) return nullptr;
        
        Node* newRoot = new Node(root->_key);
        newRoot->_left = Copy(root->_left);
        newRoot->_right = Copy(root->_right);
        
        return newRoot;
    }
    
    void _InOrder(Node* root)
    {
        if(root == nullptr) return;
        
        _InOrder(root->_left);
        cout << root->_key << " ";
        _InOrder(root->_right);
    }
    
    bool _InsertR(Node*& root, const K& key)
    {
        //最大的问题是链父，root作引用，是父结点的left/right
        if(root == nullptr)
        {
            root = new Node(key); //root是父结点的left/right的引用，这一步赋值相当于链父了
            return true;
        }
        
        if(root->_key < key)
            return _InsertR(root->_right, key);
        else if(key < root->_key)
            return _InsertR(root->_left, key);
        else
            return false;
    }
    
    bool _EraseR(Node*& root, const K& key)
    {
        if(root == nullptr) return false;
        
        if(root->_key < key)
            return _EraseR(root->_right, key);
        else if(key < root->_key)
            return _EraseR(root->_left, key);
        else
        {
            Node* del = root;
            
            if(root->_left == nullptr)
                root = root->_right; //托孤（右孩子）
            else if(root->_right == nullptr)
                root = root->_left; //托孤（右孩子）
            else
            {
                Node* minRight = root->_right;
                while(minRight->_left)
                    minRight = minRight->_left;
                //交换法：直接找key删，没法删，找替换节点交换，交换后可以删替换节点
                //(因为是最左/最右结点，一定有一侧是空的，也就可以托孤)
                swap(root->_key, minRight->_key);
                _EraseR(root->_right, key);
            }
            
            delete del;
            
            return true;
        }
    }
    
    bool _FindR(Node*& root, const K& key)
    {
        if(root == nullptr) return false;
        
        if(root->_key < key)
            return _FindR(root->_right, key);
        else if(key < root->_key)
            return _FindR(root->_left, key);
        else
            return true;
    }
    
    
    Node* _root = nullptr;
};

今天的分享就到这里了，感谢您能看到这里。

这里是培根的blog，期待与你共同进步！

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/533327.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

《花雕学AI》不用花钱，也能和ChatGPT聊天！快来看看这五个免费客户端吧

《花雕学AI》不用花钱，也能和ChatGPT聊天！快来看看这五个免费客户端吧

引言 你有没有想过和一个智能的聊天机器人对话&#xff1f;一个可以陪你聊天、讲故事、写代码、模仿名人、生成歌词等等的聊天机器人&#xff1f;如果你有这样的想法&#xff0c;那么你一定要了解ChatGPT。ChatGPT是一个由OpenAI开发的人工智能聊天机器人程序&#xff0c;它使用…
阅读更多...
基于Ajax+JSon的表格数据浏览【简单版--没连接数据库】+【连接数据库版】

基于Ajax+JSon的表格数据浏览【简单版--没连接数据库】+【连接数据库版】

目录 基于AjaxJSon的表格数据浏览【简单版--没连接数据库】 代码&#xff1a; ajax.js ch10_4.jsp student.java Query.java 运行结果&#xff1a; 点击获取表格后&#xff1a; 基于AjaxJSon的表格数据浏览【简单版--没连接数据库】 代码&#xff1a; ajax.js //声明XM…
阅读更多...
【案例实战】SpringBoot3.x自定义封装starter实战

【案例实战】SpringBoot3.x自定义封装starter实战

1.starter背景简介及作用 &#xff08;1&#xff09;什么是starter starter是SpringBoot中的一个新发明&#xff0c;它有效的下降了项目开发过程的复杂程度&#xff0c;对于简化开发操做有着很是好的效果。 starter的理念&#xff1a;starter会把全部用到的依赖都给包含进来&a…
阅读更多...
三极管的几点应用

三极管的几点应用

三极管有三个工作状态&#xff1a;截止、放大、饱和&#xff0c;放大状态很有学问也很复杂&#xff0c;多用于集成芯片&#xff0c;比如运放&#xff0c;现在不讨论。其实&#xff0c;对信号的放大&#xff0c;我们通常用运放处理&#xff0c;三极管更多的是当做一个开关管来使…
阅读更多...
微信小程序入门05-用户登录注册接口开发

微信小程序入门05-用户登录注册接口开发

用户登录注册&#xff0c;我们先需要开发后端的接口&#xff0c;接口一般需要有入参&#xff0c;然后和数据库进行交互。 1 创建表 我们现在先实现用户的登录及注册&#xff0c;建表语句 create database diancan; use diancan; CREATE TABLE users (id INT AUTO_INCREMENT …
阅读更多...
软件设计模式介绍与入门

软件设计模式介绍与入门

目录 1、软件设计模式的起源 2、什么是设计模式&#xff1f; 2.1、设计模式的设计意图 2.2、设计模式的分类准则 3、为什么要学习设计模式 4、如何学习设计模式 5、最后 VC常用功能开发汇总&#xff08;专栏文章列表&#xff0c;欢迎订阅&#xff0c;持续更新...&#x…
阅读更多...
毕业论文写作技巧

毕业论文写作技巧

毕业论文的组成部分目录自定义目录 摘要&#xff08;Abstract&#xff09;绪论相关工作&#xff08;Related work&#xff09;研究方法和结果&#xff08;Method and Results&#xff09;研究方法研究结果 结论&#xff08;Conclusion&#xff09; 写好一篇论文其实就是讲好一个…
阅读更多...
批量查询域名历史软件-域名历史快照查询工具

批量查询域名历史软件-域名历史快照查询工具

批量查询域名历史和域名历史快照 批量查询域名历史和域名历史快照是一种可以为您提供有关域名历史信息的工具&#xff0c;以下是该主题的详细介绍。 什么是域名历史&#xff1f; 域名历史记录是指域名在被注册前或过去的使用期间所经历的所有事件的记录。这些事件可能包括域…
阅读更多...
SpringBoot拦截器获取Request的body数据

SpringBoot拦截器获取Request的body数据

1. 场景 自定义Token后&#xff0c;需要在拦截器中进行token验证。在验证的过程中需要读取HttpServletRequest的body部分数据进行验证。 2. 存在问题 如果直接配置拦截器进行urlPatterns拦截&#xff0c;并进行参数验证&#xff0c;在拦截器中获取request的输入流&#xff0c…
阅读更多...
智能防盗防偷门锁语音方案设计

智能防盗防偷门锁语音方案设计

智能锁主要功能 防撬报警功能&#xff08;非必须&#xff0c;但很实用&#xff09;&#xff1a;防撬报警功能可以说是指纹密码锁功能中对提升家居安全有效的功能之一。当指纹锁受到外暴力破坏时&#xff0c;就会自动发出警报声&#xff0c;提醒小区安保。好一点的甚至可以自动…
阅读更多...
【AUTOSAR】【以太网】UdpNM

【AUTOSAR】【以太网】UdpNM

目录 一、概述 二、限制与约束 三、功能说明 3.1 协调算法 3.2 操作模式 3.2.1 Network Mode 3.2.2 准备总线睡眠模式 3.2.3 准备总线睡眠模式 3.3 网络状态 3.4 初始化 3.5 通信调度 3.5.1 NM消息发送 3.5.2 NM消息接收 3.6 其他功能 3.7 帧结构 四、API接口 …
阅读更多...
创新案例 | 肆拾玖坊白酒0到20亿增长是传销还是创新

创新案例 | 肆拾玖坊白酒0到20亿增长是传销还是创新

01.背景介绍 中国证券报引用公开数据显示&#xff0c;2016年&#xff0c;规模以上白酒企业数量为1578家&#xff0c;2021年&#xff0c;这一数字下降到965家。 同时&#xff0c;白酒产能逐年向优势产区集中&#xff0c;头部企业市场占有率不断提高。2021年&#xff0c;茅台、…
阅读更多...
性能测试-操作和优化分析

性能测试-操作和优化分析

打流工具 iperf 测试吞吐率 服务端&#xff1a;iperf -u -s 客户端&#xff1a;iperf -u -c 1.1.1.1 -b 500M -t 10 测试结果 ------------------------------------------------------------ Client connecting to 192.168.56.106, UDP port 5001 Sending 1470 byte d…
阅读更多...
全面监测健康数据，更实用的健康手表，dido E55S Pro上手

全面监测健康数据，更实用的健康手表，dido E55S Pro上手

关心健康的朋友&#xff0c;一般都特别关注自己的各项健康数据&#xff0c;会通过智能手表之类的工具来持续检测。现在健康类的智能手表选择很多&#xff0c;功能也很丰富&#xff0c;像是我现在用的这款dido E55S Pro&#xff0c;除了常规的心率、血氧之外&#xff0c;还检测心…
阅读更多...
vector【实现】：迭代器失效以及非法的间接寻址、深拷贝中的浅拷贝。

vector【实现】：迭代器失效以及非法的间接寻址、深拷贝中的浅拷贝。

vector模拟实现_云的小站的博客-CSDN博客 目录 主题&#xff1a; 迭代器失效 Insert导致的迭代器失效 ereas导致的迭代器失效 非法的间接寻址 深拷贝中的浅拷贝。 主题&#xff1a; 1&#xff09;迭代器失效 2&#xff09;非法的间接寻址 3&#xff09;深拷贝中的浅拷…
阅读更多...
2023年最佳SleekFlow最佳替代品

2023年最佳SleekFlow最佳替代品

建立更强大的对话关系的最佳平台是什么&#xff1f;现如今&#xff0c;国内客服集成与营销自动化工具也有非常多&#xff0c;比如SaleSmartly&#xff08;ss客服&#xff09;&#xff0c;被称为SleekFlow的最佳替代品。了解为什么SaleSmartly是SleekFlow的最佳替代品。在这篇文…
阅读更多...
BTC交易费激增，LTC活跃地址数飙升! BRC-20爆火背后，区块链网络经历了什么？

BTC交易费激增，LTC活跃地址数飙升! BRC-20爆火背后，区块链网络经历了什么？

BRC-20 代币和 Ordinals 协议的日益普及推动了对比特币区块空间的需求&#xff0c;比特币区块链的费用已飙升至两年来的高点。 BRC-20代币标准在 Ordinals 协议上运行。Ordinals 允许用户通过将对数字艺术的引用写入基于比特币的小型交易中&#xff0c;来将数据嵌入比特币区块…
阅读更多...
网站历史快照查询软件-批量网站历史快照查询

网站历史快照查询软件-批量网站历史快照查询

批量网站历史快照查询软件 批量网站历史快照查询软件是一种可以让用户在短时间内批量查询多个网站历史快照的工具&#xff0c;可以极大地提高用户的工作效率。批量实时查询是该软件的一大优势&#xff0c;下面主要介绍批量实时查询的优势。 一、高效性 批量实时查询可以同时…
阅读更多...
通过2种Python库，教会你如何在自动化测试时加入进度条？

通过2种Python库，教会你如何在自动化测试时加入进度条？

前言 我们在执行自动化测试或者调试时&#xff0c;自动化测试用例数量过多&#xff0c;不清楚目前用例数执行了多少个了&#xff0c;还差多少个执行完成。 这时候就会猜想&#xff0c;如果执行过程中存在进度条&#xff0c;就很清楚的了解到测试用例的执行情况&#xff0c;今…
阅读更多...
Cannot read properties of null (reading ‘content‘)报错解决

Cannot read properties of null (reading ‘content‘)报错解决

项目是用vue3webpack&#xff0c;始终启动不成功~ 一、问题报错 二、报错解决尝试总结 &#xff08;1&#xff09;首先尝试的是因为我近期在做vite3vue3的需求把node版本升到了 16.17.1 猜测是不是node版本影响的 node版本切了14.15.3&#xff0c;16.17.1&#xff0c;以及很…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023