title: 数据结构lab2-树型结构的建立与遍历
date: 2023-05-16 11:42:26
tags: 数据结构与算法
哈尔滨工业大学计算机科学与技术学院
实验报告
课程名称:数据结构与算法
课程类型:必修
实验项目:树型结构的建立与遍历
实验题目:二叉树存储结构的建立与遍历
实验日期:2021.10.27
班级:2003001
学号:120L021011
姓名:石卓凡
| 设计成绩 | 报告成绩 | 指导老师 |
|---|---|---|
一、 实验目的
\1. 掌握树的链式存储方式及其操作实现(创建、遍历、查找等)。
\2. 掌握二叉树用不同方法表示所对应的不同输入形式。
\3. 掌握二叉树中各种重要性质在解决实际问题中的应用。
\4. 掌握哈夫曼树的构造方法及其编码方法。
\5. 掌握二叉排序树的特性及其构造方法。
二、实验要求及实验环境
1**.****编**写建立二叉树的二叉链表存储结构(左右链表示)的程序,并以适当的形式显示和保存二叉树;
2.采用二叉树的二叉链表存储结构,编写程序实现二叉树的先序、中序和后序遍历的递归和非递归算法以及层序遍历算法,并以适当的形式显示和保存二叉树及其相应的遍历序列;
3**.给定一个二叉树,** 编写算法完成下列应用:(二选一)
(1)判断其是否为完全二叉树;
(2)求二叉树中任意两个结点的公共祖先。
实验环境:
操作系统:Win7/Win10
集成开发环境:devcpp++
外部库:暂无
二、 设计思想(本程序中的用到的所有数据类型的定义,主程序的流程图及各程序模块之间的调用关系)
1. 函数功能和外部接口设计
本系统总计设计了13个函数,每个函数的功能和接口设计如下表所示:
| 序号 | 函数名 | 函数功能 | 函数参数 | 函数返回值 |
|---|---|---|---|---|
| 1 | Main | 根据order执行各函数 | 无 | 无 |
| 2 | Creat | 读入TNode.txt的信息,建立根节点为Node的二叉树 | BTreeNode* &Node | NULL |
| 3 | VLR | 前序遍历 | BTreeNode *T | NULL |
| 4 | LVR | 中序遍历 | BTreeNode *T | NULL |
| 5 | LBR | 后序遍历 | BTreeNode *T | NULL |
| 6 | LevelOrder | 层序遍历 | BTreeNode* T | NULL |
| 7 | IsWanQuanErChaShu | 判断是否为完全二叉树 | BTreeNode* T | Bool(True or false) |
| 8 | ShuZuHua | 将链式存储转为顺序数组存储 | BTreeNode* NODE,TreeList TList[],int i | NULL |
| 9 | GongGongZuXian | 求两个节点对应的最近公共组先 | TreeList TList[],char A,char B | NULL |
| 10 | PreOrder_2 | 先序遍历非递归 | BTreeNode* T | NULL |
| 11 | InOrder_2 | 中序遍历非递归 | BTreeNode* T | NULL |
| 12 | PostOrder_2 | 后序遍历非递归 | BTreeNode* T | NULL |
| 13 | Show | 图形展示二叉树 | BTreeNode* T | NULL |
| 14 | Depth | 求出树的深度 | BTreeNode* T | Int(depth) |
数据定义
typedef struct BTreeNode
{
char Value;
struct BTreeNode *Left;
struct BTreeNode *Right;
}BTreeNode;
typedef struct TreeList
{
char Value;
}TreeList;
1.逻辑设计
(1)先序递归遍历
1.如果树T不为空
1.1输出T的数据域
1.2递归的遍历左子树
1.3递归的遍历右子树
(2)中序递归遍历
1.如果树T不为空
1.1递归的遍历左子树
1.2输出T的数据域
1.3递归的遍历右子树
(3)后序递归遍历
1.如果树T不为空
1.1递归的遍历左子树
1.2递归的遍历右子树
1.3输出T的数据域
(4)先序遍历非递归
\1. 如果根节点不为空则入栈
\2. While循环,当T不空或者栈不空
2.1 借助while循环沿着T左子树,并且输出当前T,一直走到最左下角的空结点
2.2 如果栈非空,则T=栈顶元素,并且弹出栈顶,进入T的右子树
2.3 在新的右子树为根节点重复上述进行遍历
(5)中序遍历非递归
\1. 如果根节点不为空则入栈
2 While循环,当T不空或者栈不空
2.1借助while循环沿着T左子树一直走到最左下角的空结点
2.2如果栈非空,则T=栈顶元素,并且弹出栈顶,并且输出当前T,进入T的右子树
2.3在新的右子树为根节点重复上述进行遍历
(6)后序遍历非递归
\1. 如果根节点不为空则入栈
\2. While循环,当T不空或者栈不空
2.1如果T不空则一直T=T的左子树,并且进栈
2.2如果T为空,T等于栈顶元素,并且弹出栈顶元素,考虑T的右子树,如果右子树存在且从未访问过,则最右子树进行后序遍历。否则,输出当前的T,并且用r记录当前的T,令T=NULL进行下一次循环
(7)层序遍历
\1. 如果根节点不为空则入队
\2. 循环直到队列为空
2.1 q=队头元素且出队,cout<<q;
2.2 如果q有左儿子则入队
2.3 如果q有右儿子则入队
(8)判断是否为完全二叉树
\1. 如果根节点不为空则入队
\2. 循环直到队列为空
2.1 如果左右孩子都有,直接左右孩子入队
2.2 如果左孩子为空,右孩子不为空,则不是完全二叉树
2.3 如果左孩子不为空,有孩子为空 ,或者如果左右孩子都为空,则从此以后访问到的结点都必须是叶子结点。如果此后出现非叶子结点,则不是完全二叉树
(9)求两个节点对应的最近公共组先
\1. 利用递归将链式存储转为数组存储
1.1 如果传入的NODE不为空,则将Value和传入的下标i,对应存入数组,并且再次调用函数,将NODE的左右儿子及其对应下标传入函数
1.2如果传入的NODE为空,则Value为#
\2. While循环直到找到公共祖先
2.1 将两个结点下标较大的除以2,将其下标指向其父节点下标
2.2 当两个节点下标相同时候,结束循环
(10)图形展示二叉树
\1. 如果根节点不为空则入队,同时利用Depth求出树的深度
\2. While直到所有都已经成功输出
2.1 len记录当前队里size代表这一层有多少个结点
2.2 While将当前这一层的所有节点输出,将左右子树入队,并且左右子树为空时候NEW一个节点将Value设为#,利用深度控制输出次数
(11)创建二叉树
\1. 文件读入根结点,入队
\2. 如果根节点不空
2.1 弹出队列首元素,读入左儿子,入队
2.2 读入右儿子,入队
2.3 借队列依次重复读入
(12)求出树的深度
\1. 如果结点存在,则递归调用返回左右子树最大值+1
\2. 如果节点不存在,直接return 0
2.物理设计
1.BTreeNode用到左右儿子链式存储,链表结点中储存了Value值, BTreeNode *Left指向该节点的左儿子,BTreeNode *Right指向该节点的右儿子
2.TreeList用到左右儿子顺序存储,存储了Char型的Value,代表这个树节点的value值,下标关系代表和其他节点相应的父子关系
3.stack栈用链式存储,栈有指向头节点的指针Node *head指向最初进入的元素(栈底),指向尾结点的Node *p,p指向栈顶最新进入的元素,记录栈元素数量的int length,而每个Node节点有对应数据类型的data,指向下一个结点的Node *next,
4.queue队列用链式存储,有指向队首的指针Node *head,指向队尾的指针Node *rear,记录队列元素多少的int length,而每一个Node结点内部都有,对应数据类型的data,指向下一个结点的Node *next
\3. 主程序流程图及各程序模块之间的调用关系
\4.
流程图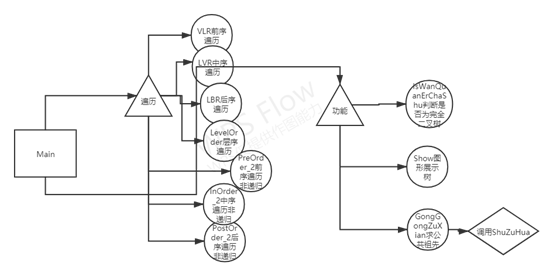
调用关系
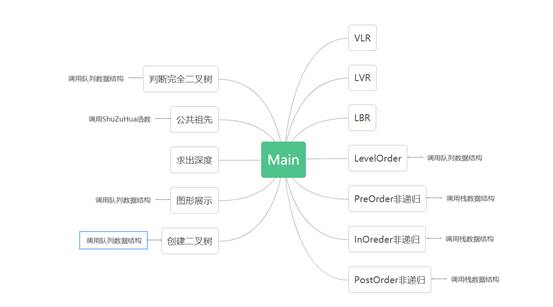
**四、**测试结果
样例1:
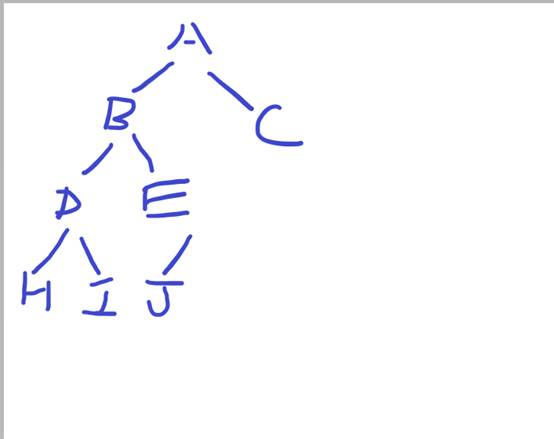
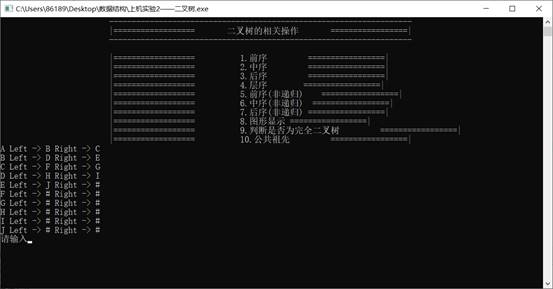
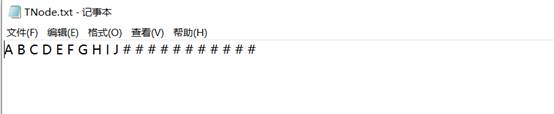
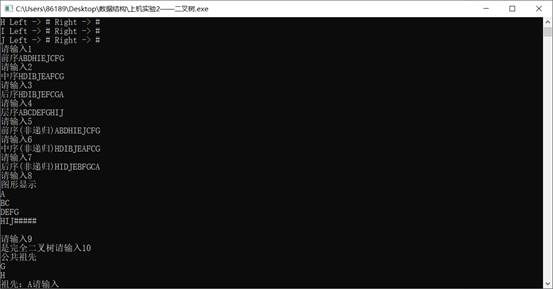

样例2**:**
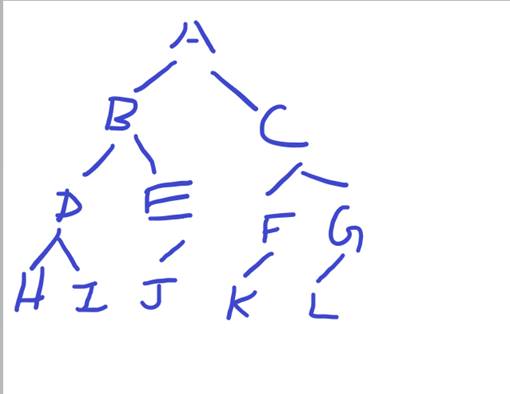
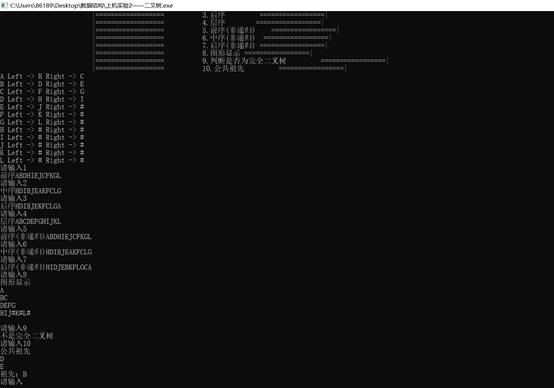


**五、**经验体会与不足
经验体会:
(1)对于遍历的非递归算法就是将递归算法利用while循环与if条件判断以及队列和栈的辅助,同一个思路写出来,递归算法简单易懂,非递归能够更进一步深入理解这种方式
(2)在求判断是否为完全二叉树等很多关于二叉树的问题都是基于遍历二叉树的算法上来做的
(3)在求公共祖先时候发现二叉树的存储方式,链式存储和数组存储各有利弊,在求公共祖先时候需要将链式转为数组,利用数组中父子结点对应下标数学关系很容易求出公共祖先
(4)在后面我们所学习到的图的深度遍历和树的先序遍历十分相似,在非递归上也都应用到栈。
过程暴露的不足:
① 对于书写非递归遍历时候,没有一个总体的把握,第一次写while循环内部判断条件总是没有考虑完全
② 解决方法:对while循环判断条件在写出程序大体框架之后再补充写出判断条件
③ 对于首次从链式存储转为数组存储树的时候非递归代码占了100多行,过于冗长
④ 解决方法:换成递归算法,直观而且简洁
**六、**附录:源代码(带注释)
**
//****文本输入样例:A B C D E F G H I J # # # # # # # # # # #**
\#include<iostream>
\#include<stdlib.h>
\#include<stdio.h>
using namespace std;
\#define MAXSIZE 100
typedef struct BTreeNode
{
char Value;
struct BTreeNode *Left;
struct BTreeNode *Right;
}BTreeNode;
typedef struct TreeList
{
char Value;
}TreeList;
template<class T>class stack
{
private:
struct Node
{
T data;
Node *next;
};
Node *head;
Node *p;
int length;
public:
stack()
{
head = NULL;
length = 0;
}
void push(T n)//入栈
{
Node *q = new Node;
q->data = n;
if (head == NULL)
{
q->next = head;
head = q;
p = q;
}
else
{
q->next = p;
p = q;
}
length++;
}
void pop()//出栈 不会!!并且不会!!!将出栈的元素返回
{
if (length <= 0)
{
abort();
}
Node *q;
T data;
q = p;
data = p->data;
p = p->next;
delete(q);
length--;
}
int size()//返回元素个数
{
return length;
}
T top()//返回栈顶元素
{
return p->data;
}
bool empty()//判断栈是不是空的
{
if (length == 0)
{
return true;
}
else
{
return false;
}
}
};
template<class T>class queue
{
private:
struct Node
{
T data;
Node *next;
};
Node *head;//!
Node *rear;//!队尾
int length;
public:
queue()
{
head = NULL;
rear = NULL;//!初始化
length = 0;
}
void push(T n)//入队
{
Node *node = new Node;
node->data = n;
node->next = NULL;//!
if (head == NULL)
{
head = node;
rear = node;
}
else
{
rear->next = node;
rear = node;
}
length++;
}
void pop()//出栈 不会!!并且不会!!!将出栈的元素返回
{
if (length <= 0)
{
abort();
}
Node *temp = head;
head = head->next;
delete (temp);
length--;
}
int size()//返回元素个数
{
return length;
}
T front()//!返回队首元素
{
return head->data;
}
bool empty()//判断栈是不是空的
{
if (length == 0)
{
return true;
}
else
{
return false;
}
}
};
void Creat(BTreeNode* &Node);
void VLR(BTreeNode *T);
void LVR(BTreeNode *T);
void LBR(BTreeNode* T);
void LevelOrder(BTreeNode* T);
bool IsWanQuanErChaShu(BTreeNode* T);
void ShuZuHua(BTreeNode* NODE,TreeList TList[],int i)//将链式存储转为顺序存储 ,赋值TList[i].Value
{//利用递归的不断进行 i从1开始,为后续 父*2=左子
if(NODE)
{
TList[i].Value=NODE->Value;
ShuZuHua(NODE->Left,TList,2*i);
ShuZuHua(NODE->Right,TList,2*i+1);
}
else//NODE==NULL,赋值#后当前这一层结束
{
TList[i].Value='#';
}
}
void GongGongZuXian(TreeList TList[],char A,char B)//寻找A与B公共祖先
{
int Father=-1;//公共祖先下标
int Anum=-1;//A下标
int Bnum=-1;//B下标
for(int i = 1;i<MAXSIZE;i++)
{
if(A==TList[i].Value)
Anum=i;
if(B==TList[i].Value)
Bnum=i;
}//寻找A B下标
while(1)//寻找公共祖先,利用儿子/2=父亲的数字关系,类似解方程
{
if(Anum==Bnum)
{
cout<<"祖先:"<<TList[Anum].Value;
return;
}
else if(Anum>Bnum)
{
Anum=Anum/2;
}
else if(Bnum>Anum)
Bnum=Bnum/2;
}
}
void Creat(BTreeNode* &Node)//层次建立
{
FILE *p;
FILE *pout;
if((pout=fopen("TNodeOut.txt","a"))==NULL)
{
cout<<"文件打开失败";
exit(0);
}
if((p=fopen("TNode.txt","r"))==NULL)
{
cout<<"文件打开失败";
exit(0);
}
queue<BTreeNode*> que;
char Value;
fscanf(p,"%c ",&Value);
//先对第一个根结点进栈处理,原因1,&Node会一起把Node地址修改,原因2方便栈循环有第一个元素
if(Value=='#')//代表空
{
Node=NULL;
return;
}
else//!='#'
{
Node = new BTreeNode;
Node->Value = Value;
que.push(Node);
}
while(!que.empty())
{//类似层次遍历,依次,某个节点,该节点左儿子,该节点右儿子,
BTreeNode *node = que.front();//读取队列里的待取元素,来依次赋值该元素的左右儿子
que.pop();
printf("%c ",node->Value);
fprintf(pout,"%c ",node->Value);
fscanf(p,"%c ",&Value);//读取
if(Value!='#')
{
node->Left = new BTreeNode;
node->Left->Value =Value;
printf("Left -> %c ",Value);
fprintf(pout,"Left -> %c ",Value);
que.push(node->Left);
}
else//=='#',代表该元素没有左儿子
{
node->Left=NULL;
printf("Left -> %c ",Value);
fprintf(pout,"Left -> %c ",Value);
}
fscanf(p,"%c ",&Value);
if(Value!='#')
{
node->Right = new BTreeNode;
node->Right->Value =Value;
printf("Right -> %c \n",Value);
fprintf(pout,"Right -> %c \n",Value);
que.push(node->Right);
}
else//=='#'
{
node->Right=NULL;
printf("Right -> %c \n",Value);
fprintf(pout,"Right -> %c \n",Value);
}
}
fclose(p);
fclose(pout);
}
void VLR(BTreeNode *T)//前序遍历
{
if(T==NULL)
return ;
else
{
cout<<T->Value;
VLR(T->Left);
VLR(T->Right);
}
}
void LVR(BTreeNode *T)
{
if(T==NULL)
{
return;
}
else
{
LVR(T->Left);
cout<<T->Value;
LVR(T->Right);
}
}
void LBR(BTreeNode* T)
{
if(T==NULL)
{
return;
}
else
{
LVR(T->Left);
LVR(T->Right);
cout<<T->Value;
}
}
void LevelOrder(BTreeNode* T)
{
FILE *pout;
if((pout=fopen("TNodeOut.txt","a"))==NULL)
{
cout<<"文件打开失败";
exit(0);
}
fprintf(pout,"层序遍历:");
if(T ==NULL)
return ;
queue<BTreeNode*> que;
que.push(T);//先处理根节点方便之后走循环while
while(!que.empty())
{
BTreeNode* t;
t=que.front();
que.pop();
fprintf(pout,"%c",t->Value);
cout<<t->Value;
if(t->Left!=NULL)
que.push(t->Left);
if(t->Right!=NULL)
que.push(t->Right);
}
fprintf(pout,"\n");
fclose(pout);
}
void PreOrder_2(BTreeNode* T)
{
FILE *pout;
if((pout=fopen("TNodeOut.txt","a"))==NULL)
{
cout<<"文件打开失败";
exit(0);
}
fprintf(pout,"前序遍历:");
if(T==NULL)
return;
stack<BTreeNode*> s;
while(T||!s.empty())//如果只有s.empty()一个判断条件,第一个就进入不了while循环
{//从自己这个结点和左子树先cout干净
while(T)
{
fprintf(pout,"%c",T->Value);
cout<<T->Value;
s.push(T);
T=T->Left;
}//最后一个进栈,然后T=null,
if(!s.empty())
{//这三句话是最终目的返回上一级的右子树,并对其前序遍历
T=s.top();//返回上一级已经cout,在下面马上进入未访问过右子树
s.pop();
T=T->Right;//进入右子树,如果右儿子不为空√,如果右儿子为NULL,在下一次while进行没有push,只有T.top(),正好用光栈一个节点返回一次的机会
}
}
fprintf(pout,"\n");
fclose(pout);
}
void InOrder_2(BTreeNode* T)
{
FILE *pout;
if((pout=fopen("TNodeOut.txt","a"))==NULL)
{
cout<<"文件打开失败";
exit(0);
}
fprintf(pout,"中序遍历:");
if(T==NULL)
return;
stack<BTreeNode*> s;
while(T||!s.empty())
{
while(T)
{
s.push(T);
T=T->Left;
}
if(!s.empty())
{
T=s.top();
s.pop();
fprintf(pout,"%c",T->Value);
cout<<T->Value;
T=T->Right;
}
}
fprintf(pout,"\n");
fclose(pout);
}
void PostOrder_2(BTreeNode* T)
{
if(T==NULL)
return;
BTreeNode* r=NULL; //r为最近访问过的结点
stack<BTreeNode*> s;
//进行对每个子树来后序遍历
while(T||!s.empty())
{
if(T)
{
s.push(T);
T=T->Left;
//一直左,然后到T=NULL
}
else //T=NULL 看返回之后是否能右转
{
T=s.top();//T=最左下方的非NULL结点,T没有左子树
if(T->Right&&r!=T->Right)//1,右子树存在且从来没有访问输出过
{
T=T->Right;//然后会进入下一次循环的if(T),s.push(T),对其这个以新的T进行后续遍历
}
else//2,没有右子树 ,或者已经访问输出过
{
s.pop();//只有当从右儿子回来时或者没有右儿子,满足后序,才弹出当前根节点,不会再回来
cout<<T->Value;//只有当从右儿子回来时或者没有右儿子,满足后序,才弹出当前根节点,不会再回来
r=T;//记录最近访问的结点,用来判断
T=NULL; //下一次循环中进入T=s.top(); ,不能直接 T=s.top()否则进入if(T)
}
}
}
}
bool IsWanQuanErChaShu(BTreeNode* T)
{
if(T==NULL)
return false;//树为空返回错 空树这里认为不是完全二叉树
queue<BTreeNode*>q;
q.push(T);
while(!q.empty())
{
BTreeNode* Top = q.front();
if(Top->Left&&Top->Right)//1如果左右孩子都有,直接记录
{
q.pop();
q.push(Top->Left);
q.push(Top->Right);
}
if(Top->Left==NULL&Top->Right!=NULL)//2如果该节点左孩子为空,右孩子不为空,则一定不是完全二叉树
{
return false;
}
if((Top->Left&&Top->Right==NULL)||(Top->Left==NULL&&Top->Right==NULL))
{//3如果该节点左孩子不为空,右孩子为空或者该节点为叶子节点,则该节点之后的所有结点都是叶子节点
q.pop();//则该节点之后的所有结点都是叶子节点
if(Top->Left)
q.push(Top->Left);
//缩减为判断当前队列里面是不是都是叶子
while(!q.empty())
{
Top=q.front();
if(Top->Left==NULL&Top->Right==NULL)
{
q.pop();
}
else
{
return false;
}
}
return true;
}
}
return true;
}
int Depth(BTreeNode* T)//求树高
{
if(T)
return max(Depth(T->Left),Depth(T->Right))+1;
else
return 0;
}
void Show(BTreeNode* T)//图形展示
{
int TDepth = Depth(T);//高度
if(T==NULL)
return;
queue<BTreeNode*> q;//不设queue设成deque才有迭代器it
q.push(T);
while(1)
{
int len=q.size();//记录当前这一层有多少个结点
if(TDepth==0)//利用深度控制输出每一层次数
break;
while(len>0)
{
T =q.front();
q.pop();
cout<<T->Value;
if(T->Left)
q.push(T->Left);
else
{
BTreeNode* temp;
temp=new BTreeNode;
temp->Value='#';
temp->Left=NULL;
temp->Right=NULL;
q.push(temp);
}//NULL就新建立一个'#'也入栈
if(T->Right)
q.push(T->Right);
else
{
BTreeNode* temp;
temp=new BTreeNode;
temp->Value='#';
temp->Left=NULL;
temp->Right=NULL;
q.push(temp);
}//NULL就新建立一个'#'也入栈
len--;
}//这里为一层
cout<<endl;//当前这一层结束
TDepth--;
}
}
int main()
{
BTreeNode* T;
TreeList TList[MAXSIZE];
int n;
cout<<" -------------------------------------------------------------------\n";
cout<<" |================== 二叉树的相关操作 =================|\n";
cout<<" -------------------------------------------------------------------\n\n";
cout<<" |================== 1.前序 =================|\n";
cout<<" |================== 2.中序 =================|\n";
cout<<" |================== 3.后序 =================|\n";
cout<<" |================== 4.层序 =================|\n";
cout<<" |================== 5.前序(非递归) =================|\n";
cout<<" |================== 6.中序(非递归) =================|\n";
cout<<" |================== 7.后序(非递归) =================|\n";
cout<<" |================== 8.图形显示 =================|\n";
cout<<" |================== 9.判断是否为完全二叉树 =================|\n";
cout<<" |================== 10.公共祖先 =================|\n";
Creat(T);
while(1)
{
cout<<"请输入";
cin>>n;
switch(n)
{
case 1:
cout<<"前序";
VLR(T);
cout<<endl;
break;
case 2:
cout<<"中序";
LVR(T);
cout<<endl;
break;
case 3:
cout<<"后序";
LBR(T);
cout<<endl;
break;
case 4:
cout<<"层序";
LevelOrder(T);
cout<<endl;
break;
case 5:
cout<<"前序(非递归)";
PreOrder_2(T);
cout<<endl;
break;
case 6:
cout<<"中序(非递归)";
InOrder_2(T);
cout<<endl;
break;
case 7:
cout<<"后序(非递归)";
PostOrder_2(T);
cout<<endl;
break;
case 8:
cout<<"图形显示\n";
Show(T);
cout<<endl;
break;
case 10:
cout<<"公共祖先"<<endl;
ShuZuHua(T,TList,1);//提前转为顺序存储方便用下标
char C1,C2;
cin>>C1>>C2;
GongGongZuXian(TList,C1,C2);//利用下标找
cout<<"\n";
break;
case 9:
if(IsWanQuanErChaShu(T)==true)
cout<<"是完全二叉树\n";
else
cout<<"不是完全二叉树\n";
break;
}
}
}