🪐9.6 偏序
- 1、⛺偏序关系和偏序集
- ⛲偏序关系
- ⛲偏序(关系)的例子
- a. “大于或等于” 关系
- b. “整除” 关系
- c. “包含” 关系
- 🎬偏序集
- 🎬可比性(comparability)
- " ≼ " 符号
- a. 可比 & 不可比
- b. 全序( =线序 )
- c. 良序集、良序归纳原理及其应用
- 🎬偏序集的例子
- a. 可比
- b. 全序
- c. 良序集
- 2、⛺字典序(Lexicographic Orderings)
- 3、⛺哈塞图(Hasse Diagrams)
- 构造哈塞图
- 覆盖
- 4、⛺偏序集上的特殊元素
- 极大元、极小元
- 最大元、最小元
- 上确界、下确界
- 在Hasse图中看最大元、最小元、极小元、极大元
- 5、⛺格(Lattices)
⭐这一节期末会考大题
1、⛺偏序关系和偏序集
⛲偏序关系
定义:定义在集合 S 上的关系 R,如果它是自反的、反对称的和传递的,就称为偏序(或 偏序关系)。
❗注意:在一个集合的偏序关系中,并不是任何2个元素之间都具有偏序关系,例如 aRb cRd,但是 a与c之间可能不具有偏序关系R
⛲偏序(关系)的例子
证明是否是偏序,要依次验证自反性、反对称性、传递性满足与否
a. “大于或等于” 关系
证明:“ 大于或等于 ” ( ≥ )关系是整数集合上的偏序关系。
🔴解:
自反性: 对所有整数 a 有 a ≥ a,✔️
反对称性: 如果 a ≥ b 且 b ≥ a,那么 a = b,✔️
传递性: 因为 a ≥ b 且 b ≥ c 蕴涵 a ≥ c,✔️
综上所述, ≥ 关系是整数集上的偏序关系
b. “整除” 关系
证明:“ 整除 ”( | )关系是正整数集合上的偏序关系。
🔴解:
自反性: 对所有整数 a,有 a | a,✔️
反对称性: 如果 a 和 b 是正整数,且有 a | b 和 b | a,那么 a = b,✔️
传递性: 假设 a 整除 b 并且 b 整除 c。则有正整数 k 和 l 使得 b = ak 和 c = bl 成立。因此,c = a(kl),所以 a 整除 c,✔️
综上所述, 整除 关系是正整数集合上的偏序关系
c. “包含” 关系
证明:集合的包含(⊆)关系 是定义在集合 S 的幂集上的偏序。
🔴解:
自反性: 只要 A 是 S 的子集,就有 A ⊆ A,✔️
反对称性: A ⊆ B 和 B ⊆ A 蕴涵 A = B,✔️
传递性: A ⊆ B 和 B ⊆ C 蕴涵 A ⊆ C,✔️
综上所述, 包含关系是定义在集合 S 的幂集上的偏序。
🎬偏序集
集合 S 与定义在其上的偏序关系R 一起称为偏序集,记作 (S, R)。
集合 S 中的成员称为偏序集的元素
🎬可比性(comparability)
" ≼ " 符号
符号" ≼ " 用于表示任何偏序集中的关系。
在不同的偏序集中,会使用不同的符号表示偏序,如≤、⊆ 和 │
👉然而,我们需要一个符号用来表示任意一个偏序集中的序关系:
通常,在一个偏序集 (S,R)中,记号a ≼ b表示( a , b )∈R。使用这个记号是由于 “ 小于或等于 ” 关系是偏序关系的范例,而且符号" ≼ " 和 " ≤ "很相似。
(注意符号" ≼ " 用来表示任意偏序集中的关系,并不仅仅是“小于或等于”关系)
❗当 a 与 b 是偏序集 (S, ≼ ) 的元素时,不一定有 a ≤ b 或 b ≤ a
例如,在偏序集 ( P(Z),⊆ ) 中,{1,2}与{1,3}没有关系,反之亦然,因为没有一个集合被另一个集合包含。
a. 可比 & 不可比
定义:偏序集 (S, ≼) 中的元素 a 和 b 称为可比的,如果 a ≼ b 或 b ≼ a。
当 a 和 b 是 S 中的元素并且既没有 a ≼ b,也没有 b ≼ a,则称 a 与 b 是不可比的(incomparable)。
❗注意:这里的“ ≼ ” 不同于 “ ≤ ”,写的时候要尽可能弯一点,便于区分
“ ≼ ”:![]()
“ ≤ ”:![]()
b. 全序( =线序 )
定义:如果(S, ≼)是偏序集,且 S 中的每对元素都是可比的,则 S 称为全序集(totally ordered set)或线序集(linearly ordered set),且 " ≼ " 称为全序或线序。
一个全序集也称为链(chain)
c. 良序集、良序归纳原理及其应用
良序集定义:
对于偏序集( S, ≼ ),如果 " ≼ "是全序,并且 S 的每个非空子集都有一个最小元素,就称它为良序集(well-ordered set)。
(良序是对于结构很好的全序(线序)而言的)
良序归纳原理:
设S是一个良序集。如果(归纳步骤)对所有y∈𝑆,如果 P(x) 对所有 x∈𝑆 且 x ≺ y 为真,则P(y)为真,那么P(x)对所有的 x∈𝑆 为真
(证明:假设P(x)不对所有的x∈𝑆为真。那么存在一个元素 y∈𝑆,使得P(y)为假。于是集合A = {x∈𝑆|P(x)为假} 是非空集合。因为S是良序的,所以A有最小元素a, 根据a是选自A的最小元素,对所有 x∈𝑆 且 x ≺ a 都有 P(x) 为真。由归纳步骤得P(a)为真。这个矛盾就证明了P(x)必须对所有的x∈𝑆为真。)
良序归纳原理的应用:
比数学归纳法更简单,使用良序归纳法进行证明时,不需要基础步骤
因为若 x0 是良序集的最小元素,由归纳步骤可知 P(x0) 为真。因为不存在 x∈S 且x≺x0,所以P(x) 对所有 x∈S 且 x≺x0 为真
🎬偏序集的例子
a. 可比
在偏序集 ( Z+ , | )中,整数 3 和 9 是可比的吗?5 和 7 是可比的吗?
🔴解:
整数 3 和 9 是可比的,因为 3|9
整数 5 和 7 是不可比的,因为 5不可整除7,且 7 不可整除 5
b. 全序
全序:每对元素都是可比的
①偏序集(Z,≤ )是全序集,因为只要a,b是整数,就有a ≤ b 或者b ≤ a
②偏序集(Z+,| )不是全序集,因为它包含不可比的元素,比如 3 和 5
c. 良序集
正整数的有序对的集合:Z+ × Z+,与 ≼ 构成良序集(因为存在最小元素),其中如果a1 < b1 ,或如果a1 = b1且a2 < b2 ,则(a1 ,a2 )≼(b1 ,b2 )
集合 Z 与通常的 ≤ 不是良序的,因为 Z 中包含负整数集合,而负整数集合中没有最小元素
2、⛺字典序(Lexicographic Orderings)
定义:给定两个偏序集 ( A1 , ≼1 ) 和 ( A2, ≼2 ) ,在 A1 × A2 上的字典顺序 ≼ 定义为 (a1, a2) 小于 (b1, b2),即 (a1, a2) ≺ (b1, b2),或者a1 ≺ 1 b1,或者 a1 = b1 且 a2 ≺2 b2
(把相等增加到 A1 × A2 的序 ≺ 上,就得到一个偏序 ≼ )
例:考虑由小写英语组成的字符串的集合。使用字母在字母表中的顺序,可以构造在字符串的集合上的字典顺序。这与字典中使用的顺序相同。
🔴
discreet ≺ discrete,因为字符串在第7位出现不同字母,且 e ≺ t
discreet ≺ discreetness,因为这两个字符串前8个字母相同,但是第二个字符串更长
3、⛺哈塞图(Hasse Diagrams)
**定义:**哈塞(Hasse) 图是偏序的一种可视化表示,它省略了由于自反性和传递性而必须出现的边
构造哈塞图
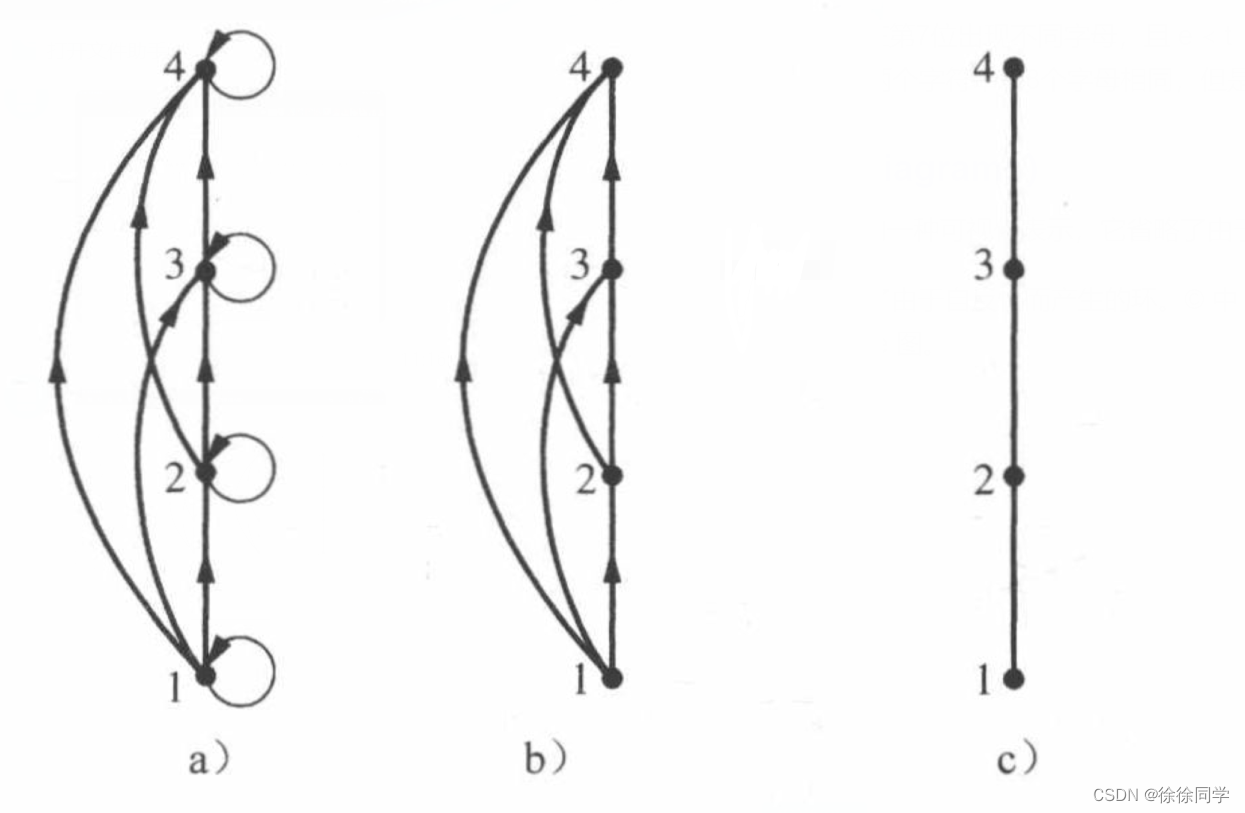
偏序如上图 (a) 所示
构造Hasse图的步骤:
① 移走 由于自反性而产生的 环( 如图 b))
② 移走 由于由于传递性而必须出现的 边( 如图c))
③最后,排列每条边使得它的 起点在终点的下面
覆盖
设 ( S, ≼ ) 是一个偏序集。若x ≺ y且不存在元素z∈S使得x ≺ z ≺ y,则称元素y∈S 覆盖 元素x∈S。
y 覆盖 x 的有序对 (x,y) 的集合称为(S, ≼ )的 覆盖关系
对应到Hasse图,即上下直接相邻连接的两个元素有覆盖关系
从对偏序集的哈塞图的描述中,我们可以看出,在(S,≤)的哈塞图中的边是指向上面的边并且与(S,≤)的覆盖关系中的有序对相对应。而且,我们可以从偏序集的覆盖关系中得到这个偏序集,因为它是它的覆盖关系的传递闭包的自反闭包。
这就告诉我们,可以从哈塞图中构造一个偏序
4、⛺偏序集上的特殊元素
极大元、极小元
极大元:假设a为极大元,则任取与a具有关系R的元素x,都有xRa.(也就是说:并不是A中的任意元素都与a有关系R,这就是最大元与极大元的区别)
极小元:假设a为极小元,则任取与a具有关系R的元素x,都有aRx.
最大元、最小元
论最大元、最小元,前提是可比!!!
最大元:偏序集中存在一个元素大于每个其他的元素。这样的元素称为最大元
( 假设a为最大元,则在集合A中,任取元素x,都有xRa )
最小元:类似地,一个元素称为最小元,当它小于偏序集的所有其他元素。
( 假设a为最小元,则在集合A中,任取元素x,都有aRx )
最大元、最小元是唯一的,极大元与极小元不唯一
上确界、下确界
A是一个偏序集,B包含于A,在哈斯图中,求B的上界、上确界,下界、下确界:
y 比 B 中所有的元素都要大,称y是B的上界。上界中最小的叫做上确界
y 比 B 中所有的元素都要小,称y是B的下界。下界中最大的叫做下确界
从哈斯图上看出 上界、上确界、下界、下确界的方法:
在A的哈斯图中,标出子集B中的结点,
则不低于(不高于)其中最高结点(最低结点)并有与它们均相连且只通过下方( 上方)直线相连 (包括环) 的结点都为B的上界(下界);
在上界集(下界集)中距B中最高结点(最低结点)路径最短的结点是上确界(下确界)
例:
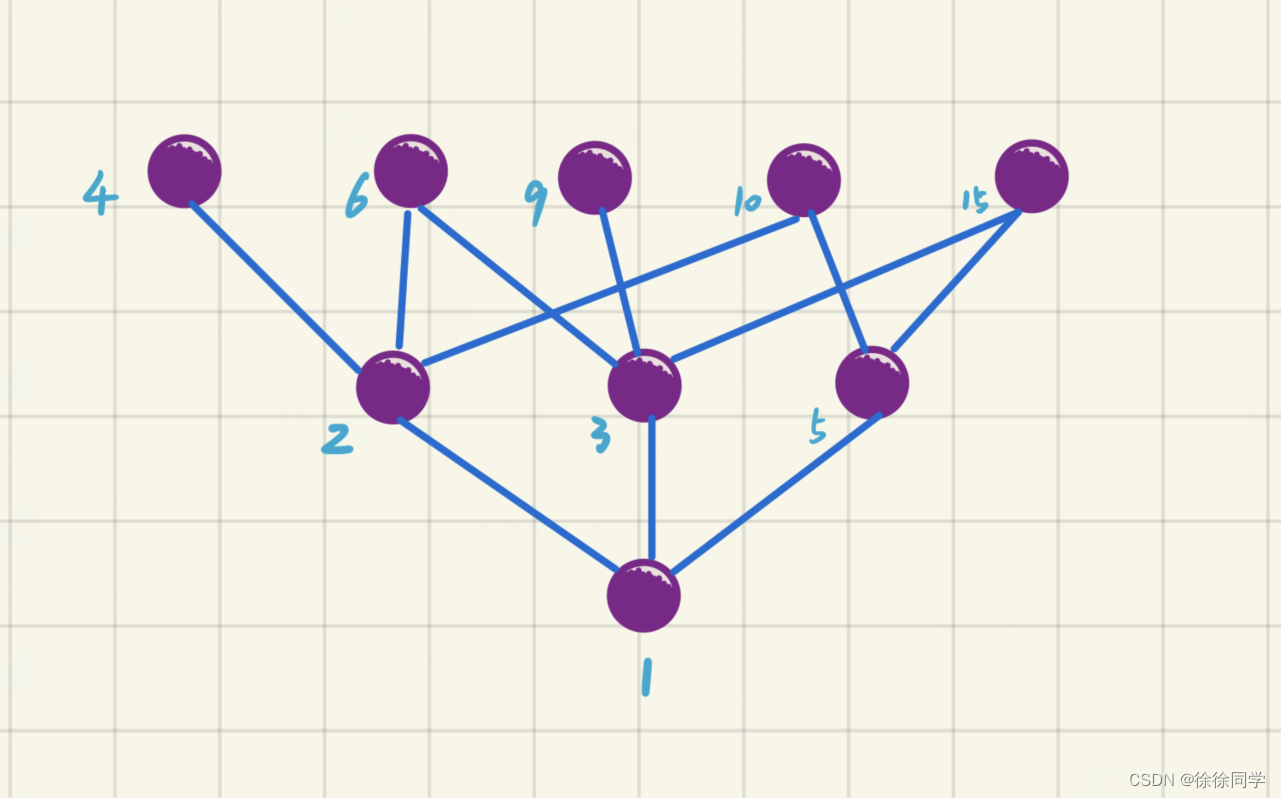
集合 A = { 1 , 2 , 3 , 4 , 5 , 6 , 9 , 10 , 15 },
(A,|)是一个偏序集,在哈斯图中,求A的上界、上确界,下界、下确界
🔴解:
A不存在上界,当然也不存在上确界;
1 比 A 中所有的元素都要小,所以 1 是 A 的下界,也是下确界
在Hasse图中看最大元、最小元、极小元、极大元
从哈斯图上看出 最大元、最小元、极小元、极大元的方法:
(以下均就A是一个偏序集而言,B包含于A,求B中的极大元、极小元、最大元、最小元)
(1)极大元:在B的哈斯图中每一个 孤立结点 或 只有下方连线的结点 是B的极大元。
(2)极小元:在B的哈斯图中每一个 孤立结点 或 只有上方连线的结点 是B的极小元。
(3)最大元和最小元:首先找出B的极大元和极小元 → 若极大元或极小元只有一个,则这个极大元或极小元就是B的最大元或最小元;若不止一个,则B的最大元或最小元不存在。
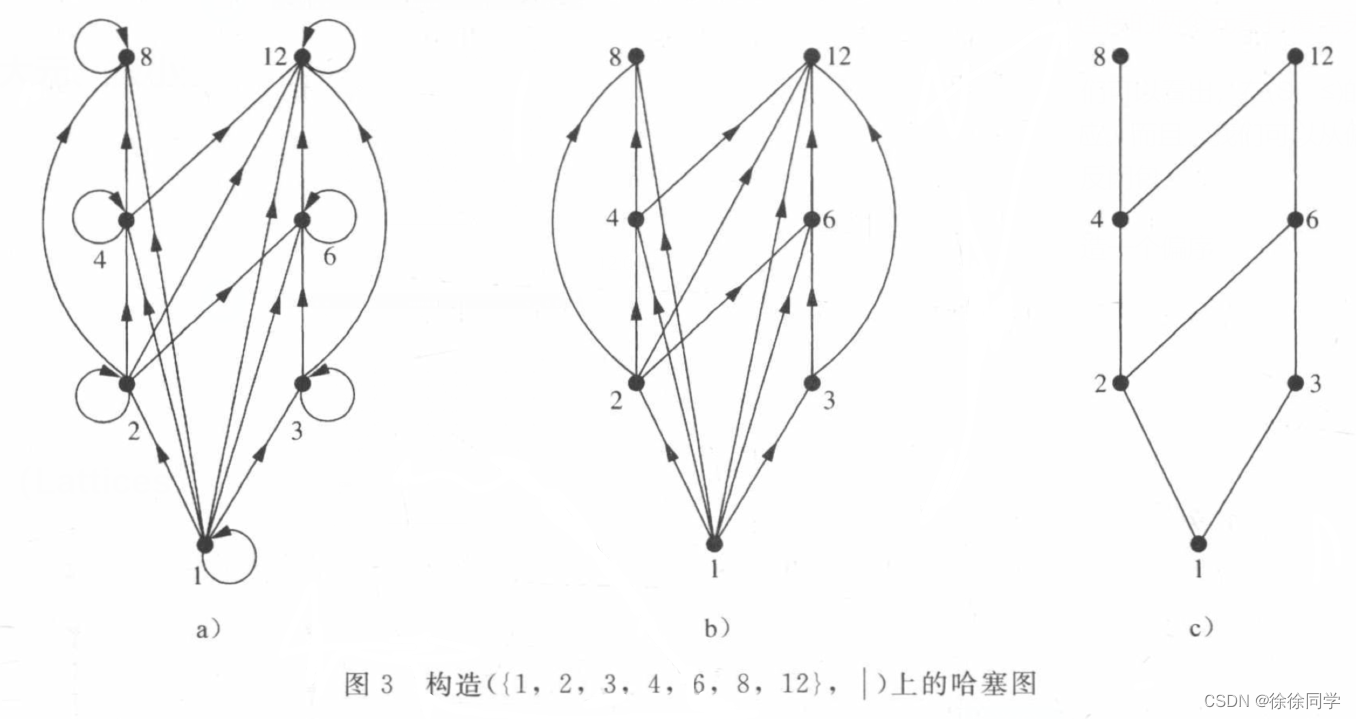
例1:偏序集 ( { 2,4,5,10,12,20,25 } ,| ) 中的哪些元素是极大元,哪些是极小元?
🔴解:
画出这个偏序集的哈塞图(如图),显示了极大元是12,20,25;极小元是2,5
(没有最大元、最小元)
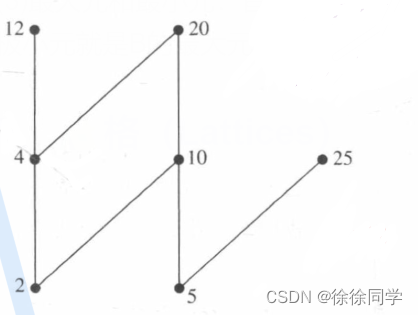
例2:
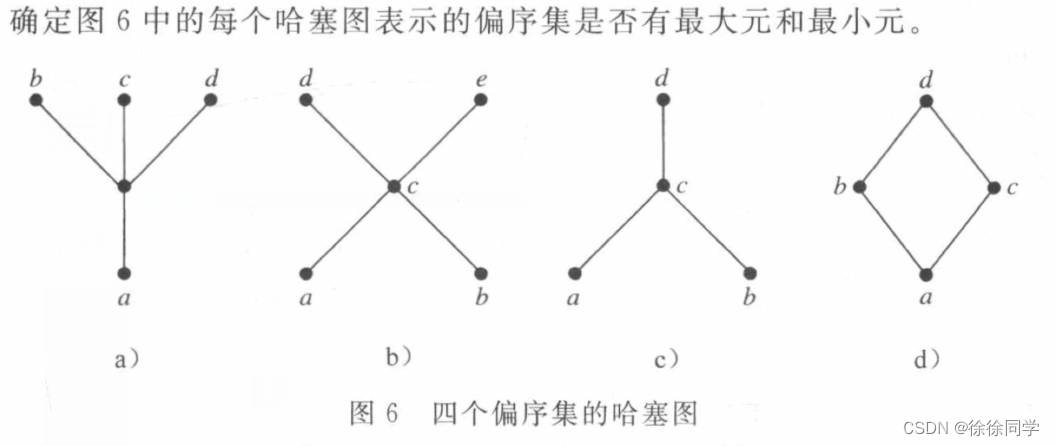 a) 没有最大元,有最小元a
a) 没有最大元,有最小元a
b)都没有
c) 最大元d,没有最小元
d)最大元是d,最小元是a
5、⛺格(Lattices)
如果一个偏序集的每对元素都有最小上界和最大下界,则称这个偏序集为格
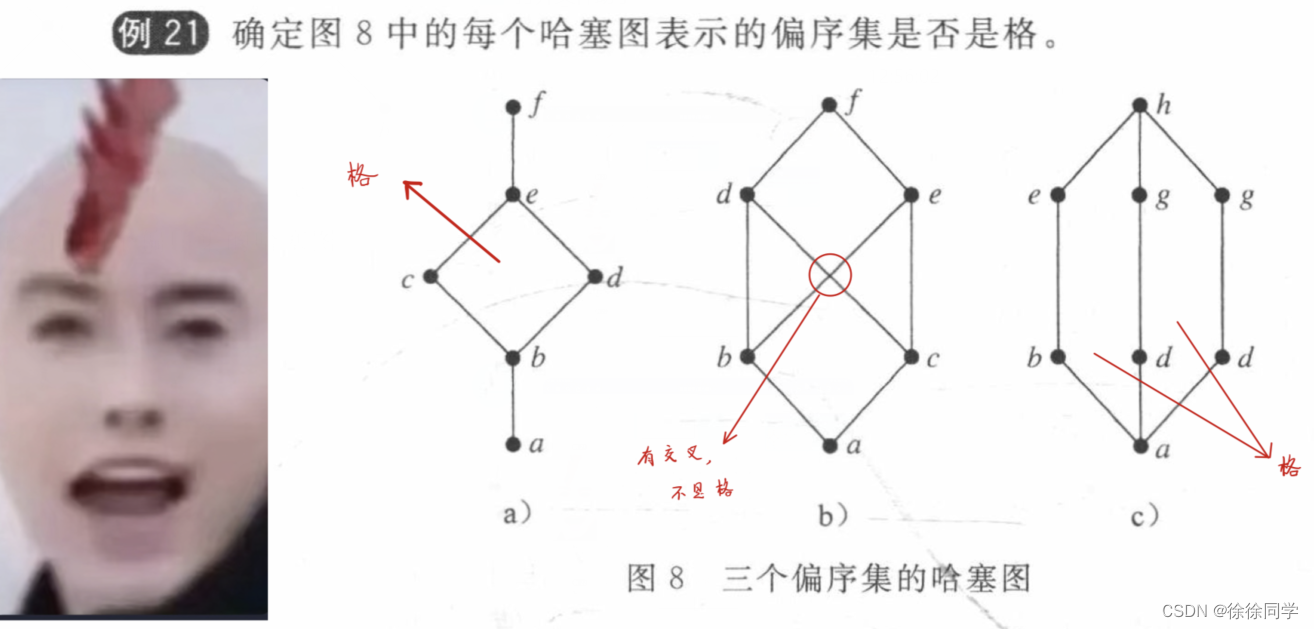
a)、c)每对元素都有最小上界和最大下界,比较好判断
对于b):
b)所示的Hasse图表示的偏序不是格,因为元素b和c没有最小上界(b,c有上界d和e,但是d、e不可比,无法确定d e哪个最小 )
(书上的几个例题:)