本文来自:GIS科研实验室
基本概念
1.什么是克里金插值?
克里金插值又称空间局部插值法,是以半变异函数理论和结构分析为基础,在有限区域内对区域化变量进行无偏最优估计的一种方法,是地统计学的主要内容之一。南非矿产工程师D.R.Krige在寻找金矿时首次运用这种方法,法国著名统计学家G.Matheron随后将该方法理论化、系统化,并命名为Kriging,即克里金方法。——引自《地理信息系统空间分析实验教程》
2.克里金插值的适用条件?
区域化变量要存在空间相关性,即半变异函数和结构分析的结果表明区域化变量存在空间相关性。
3.克里金插值需要注意的点?
-
数据应符合前提假设。例如,普通克里金要求数据变化呈正态分布。
-
数据应尽量充分,样本数尽量大于80,每一种距离间隔分类中的样本对数尽量多余10对。
-
在具体建模过程中,很多参数是可调的,且每个参数对结果的影响不同。
-
当数据足够多时,各种插值方法的效果基本相同。(我理解的数据足够多,是指数据量在500以上)
4.克里金方法的分类?
普通克里金、简单克里金、泛克里金、协同克里金、对数正态克里金、指示克里金、概率克里金和析取克里金。
下面我将以普通克里金为例,进行石家庄主城区住宅价格的克里金插值教学。普通克里金是区域化变量的线性估计,它假设数据变化呈正态分布,认为区域化变量的期望值是未知的常量。插值过程类似于加权滑动平均,权重值的确定来自于空间数据分析。
1.首先打开地统计工具条.
右键ArcGIS工具条,勾选Geostatistical Analyst模块。

图1
2.首先判断数据是否呈正态分布,如果不是,对数据进行log变换。判断数据是否呈正态分布的方法有很多种,例如:直方图和正态QQ图。我们以直方图为例进行判断。选择Geostatistical Analyst—探索数据—直方图。怎么看数据是否呈正态分布呢?在直方图提供的汇总统计数据中,如果数据服从正态分布,则平均值与中值类似,偏度应接近零,并且峰度应接近 3。如果数据高度偏斜,可选择对数据进行变换,看是否可以使数据更接近正态分布。
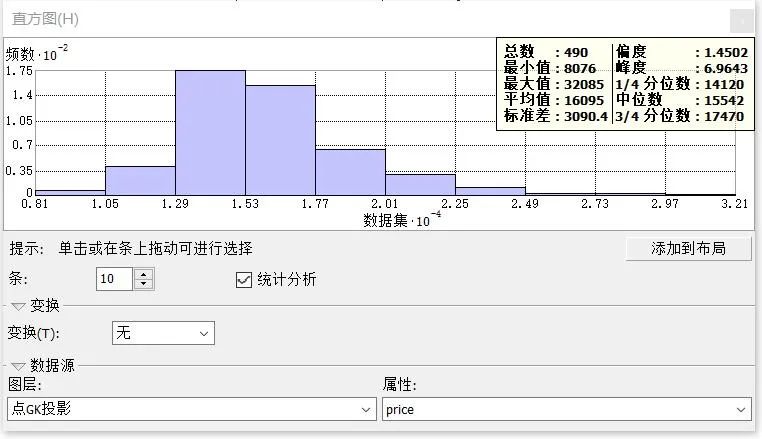
图2
我们这里的数据看起来就不是很正态,所以我们可以对数据进行log变换。选择变换—log就可以了。这下看起来就像是正态分布了,符合原假设。
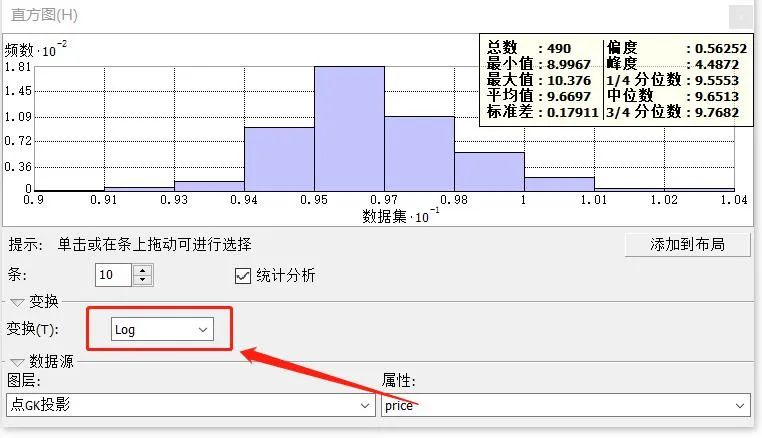
图3
3.下面对数据进行趋势面分析。选择Geostatistical Analyst—探索数据—趋势分析。

图4
4.我们可以看到在x和y方向存在明显的二阶趋势,注意在做克里金分析的时候剔除,如果你的数据在这里面是平的,并没有像示例数据这样的曲线,就不需要剔除二阶趋势(后面会讲到)

图5
还有一点需要注意,在做趋势分析的时候,你的图层和属性一定是你要分析文件的图层和属性!!!

图6
5.前期的分析工作做完了。这一部开始进行克里金插值。选择Geostatistical Analyst—地统计向导。

图7
6.选择地统计方法中的克里金法/协同克里金法,然后设置好源数据集和数据字段,点击下一步。

图8
7.这里选择使用平均值。

图9
8.这一步中,克里金法类型选择普通克里金,输出表面类型选择预测。由于我们在前面的分析中发现原始数据并不呈正态分布,只有当数据进行log变换后才呈正态分布,因此这里的变换类型选择log。还有就是在趋势分析中,我们发现数据存在二阶趋势,因此这里趋势的移除阶数选择二次。
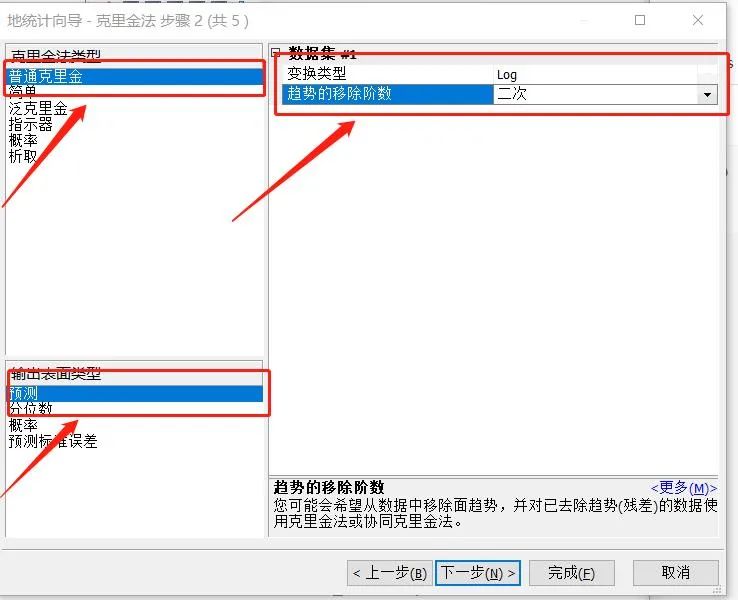
图10
9.这一步不用管,我们保持默认值就OK。

图11
10.这一步是半变异函数的设置,如果你会用GS+软件,可以根据GS+软件的计算结果来修改相关参数,如果不会你就按照我的设置来就可以了,因为我曾经比较过GS+软件计算的参数和ArcGIS自己计算的参数,结果是ArcGIS自己计算的参数效果会比较好一点。对于这一步参数的设置,我的建议是,除了各向异性选择True(各项异性就是说你的数据在各个方向的分布趋势都是不相同的,如果是近似相同的,那么此项就选择fasle),其余保持默认设置就可以了。

图12
11.下一步不用管,保持默认设置就好。

图13
12.下一步就是模型的相关参数,也是判断模型拟合度是否良好的标准。符合以下标准的模型是最优的:标准平均值最接近于0,均方根预测误差最小,平均标准误差最接近与均方根预测误差,标准均方根预测误差最接近于1。

图14
13.生成的克里金插值图如下。

图15
14.下面我们对这幅图进行美化。首先将该图裁剪至研究范围内。右键图层—属性—范围—将范围设置为(研究区域的范围,本文为矩形范围主城4区(区县,GK))

图16
15.然后就变成这样了。
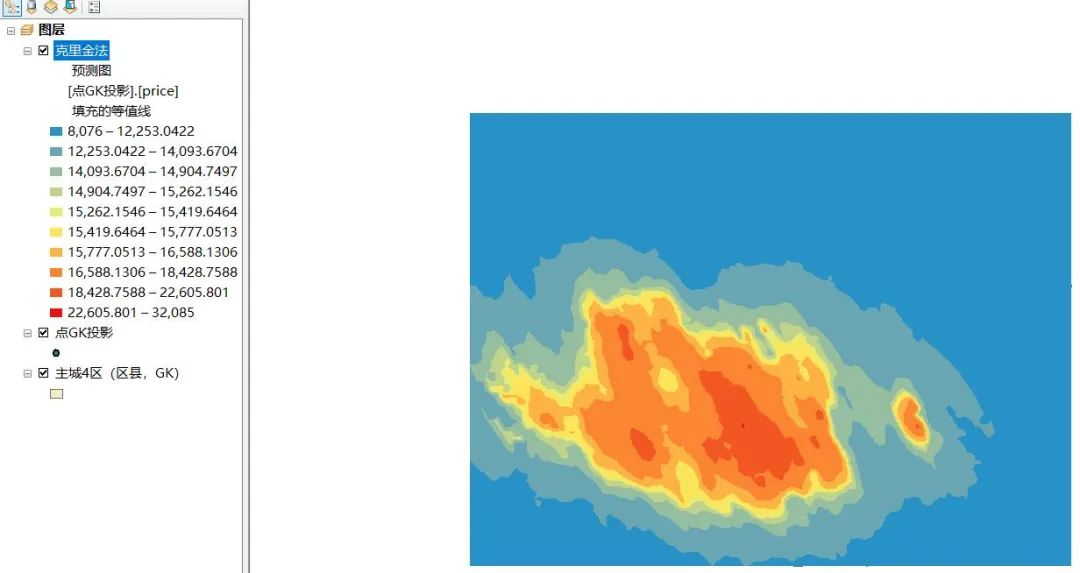
图17
16.右键图层—属性—数据框—裁剪选项—裁剪至形状—指定形状—要素的轮廓—选择研究区域图层(本文为主城4区(区县,GK))

图18
17.点击应用后,图层就会变成如下所示的样子。

图19
18.最后可以在符号系统中选择自己喜欢的色带,并加上一些特效。
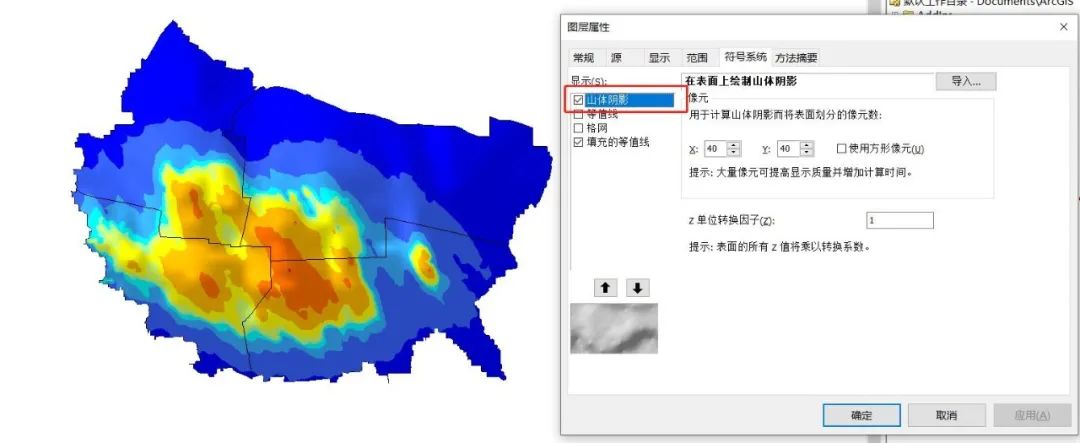
树谷资料库资源大全(4月19日更新)
树谷课堂-汇总