OWL本体语言
基于RDF语法,最规范,最严谨,表达能力最强
一 语法
三元组
二 逻辑基础
描述逻辑:基于对象的知识表示的形式化,是一阶谓词逻辑的一个可判定子集
三 描述逻辑系统
一个描述逻辑包含4个基本组成部分
1.最基本的元素:概念,关系,个体
(1)概念:解释为一个领域的子集
一元,集合,学生:{x|Student}
(2)关系:解释为一个领域的二元关系(笛卡尔乘积)
例如:{<x,y>|friend(x,y)}
(3)个体:一个领域内的实例
小明{Ming}
2.TBox术语集:泛化的知识
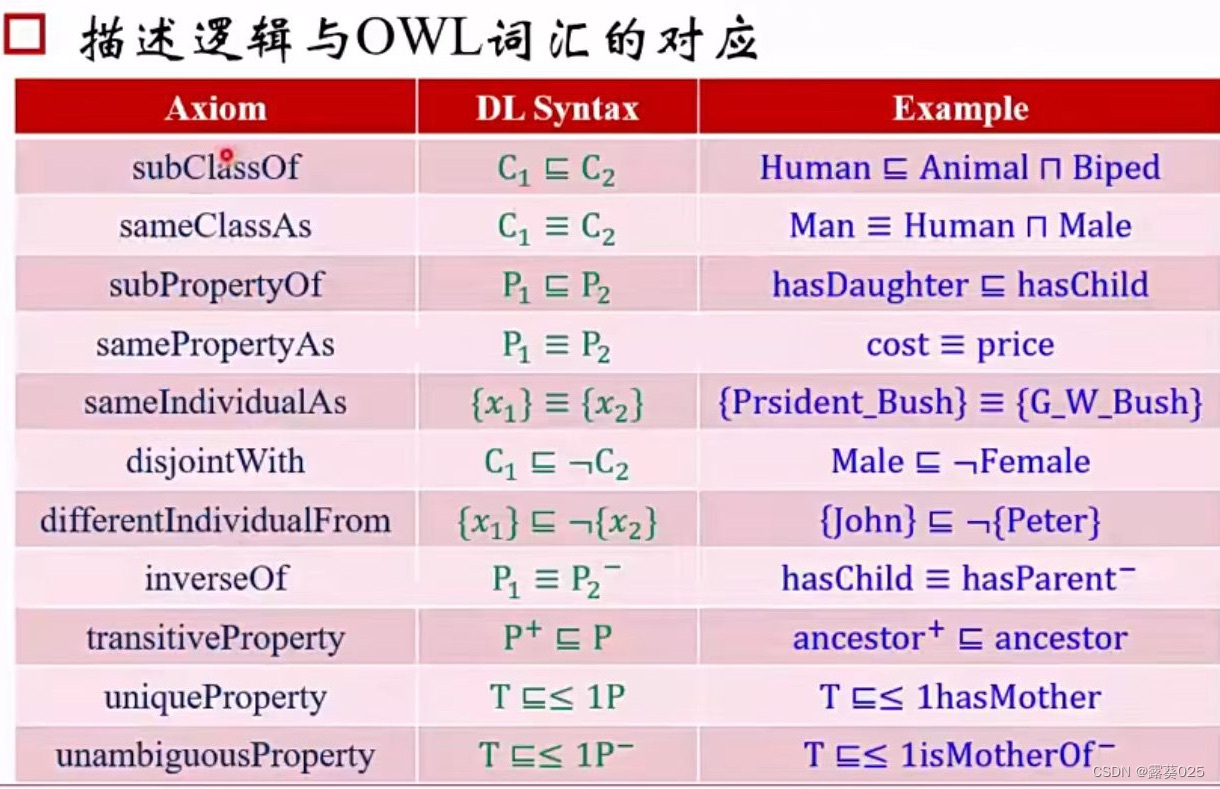
描述概念和关系的知识,被称之为公理(Axio
m),由于概念之间包含关系,TBox知识形成类似格(Lattic)的结构,这种数学结构是由包含关系决定的,与具体实现无关。
定义
引入概念以及关系名称。
例如:Mother,Person,has_Child
包含
声明包含关系的公理。
例如Mother属于 存在has_Child.Person
3.ABox断言集:具有个体的信息。
ABox包含外延知识(又称断言(Assertion)),描述论域中的特定个体。
概念断言
表示一个对象是否属于某个概念:
Mother(Alice),Person(Bob)
关系断言
表示两个对象是否满足特定关系:
has_Child(Alice,Bob)
4.TBox和ABox上的推理机制
描述逻辑知识库
K:=<T,A>
描述逻辑的语义:可满足性
解释I是知识库K的模型,当且仅当I是K中每个断言的模型。
若一个知识库K有一个模型,则称K是可满足的。
若断言A对于K的每个模型是满足的,则称K逻辑蕴含A,记为K|=A。
对于概念C,若有一个模型I使得⬇️,则称C是可满足的。

四 知识推理任务
通过各种方法获取新的知识或者结论,这些知识和结论满足意义
1.可满足性
(1)本体可满足性:
检查本体是否可满足,即是否具有模型。
(2)概念可满足性:
即检查是否具有模型,使得针对概念的解释不是空集。
2.分类
针对TBox的推理,计算新的概念包含关系。
Mother 属于 Women
Women 属于 Person
⬇️
Mother 属于 Person

3.实例化
计算属于某个概念或关系的所有实例的集合
计算新的实例信息:Mother(Alice)
Mother 属于 Women
⬇️
Women(Alice)
计算新的二元组:has_son(Alice,Bob)
has_son 属于 has_Child
⬇️
has_Child(Alice,Bob)
本体推理方法与工具介绍
1.基于Tableaux运算的方法
Tableaux运算:检查某一本体的可满足性,以及实例检测
基本思想:通过一系列规则构建Abox,以检测可满足性,或者检测某一实例是否存在与某概念,类似于一阶逻辑的归结反驳。
给定如下本体,检测实例Allen是否在Women中?
Man 交 Woman 属于 空
Man(Allen)
Woman(Allen)?——待反驳的结论
若⬆️在初始情况已经存在于原始本体,那么推导出该本体不可满足
相关工具:
| 工具 | 支持语言 |
|---|---|
| FacT++ | OWL,DL |
| Pellet | OWL,DL |
| Racer | OWL,DL |
| HermiT | OWL,2 Proflies |
2.基于逻辑编程改写的方法
(1)推理规则

(2)Datlog语言
1). 原子(Atom)
p(t1,t2,t3,…tn) p-谓词;ti:项(常量或变量);n:目数
如:has_Child(X,Y)
2). 规则(Rule)
H:-B1,B2,B3,…,Bm H:头部原子;Bn:本部原子
如:has_Child(X,Y):-has_son(X,Y)
3). 事实(Fact)
F(c1,c2,c3,…,cn):- 没有本部且没有变量的规则
如:has_Child(Alice,Bob):-
Datlog程序是规则的集合
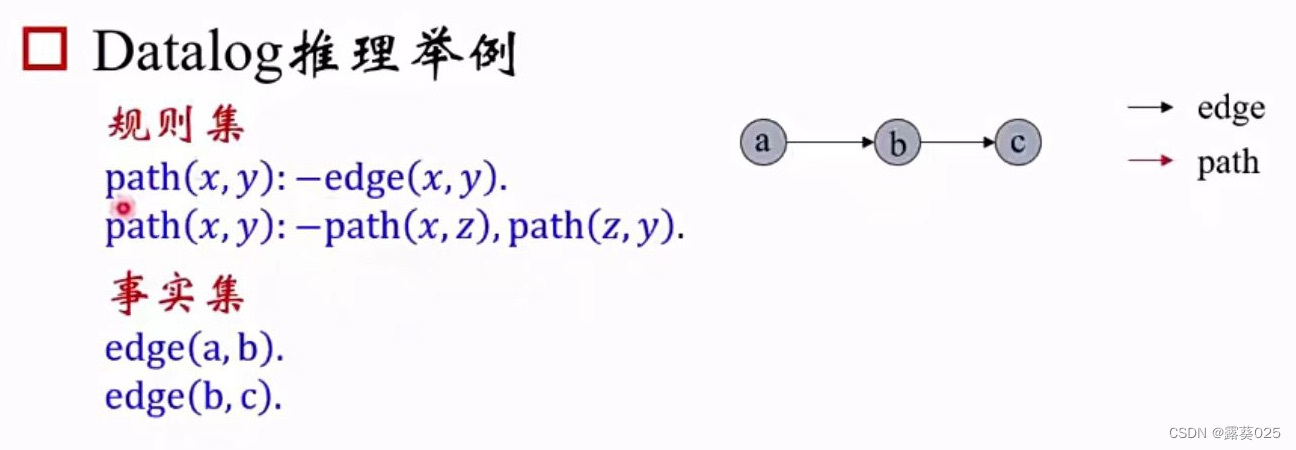
结果集:
Path(a,b)
Path(b,c)
Path(a,c)
相关工具:
| 项目 | Value |
|---|---|
| RDFox | OWL 2 RL |
| KAON2 | OWL DL/SWRL |
3.基于 一节查询重写的方法
(1)查询重写的目的:
高效地结合不同数据格式的数据源,重写方法关联起了不同的查询语言。
(2)一阶查询:
具有一阶逻辑形式的查询语言,Datalog是数据库的一种查询语言,同时具有一阶逻辑形式。
(3)针对本体基于一阶查询进行重写:
以Datalog语言为中间语言,首先重写SPARQL语言为Datalog,再将Datalog重写为SQL查询
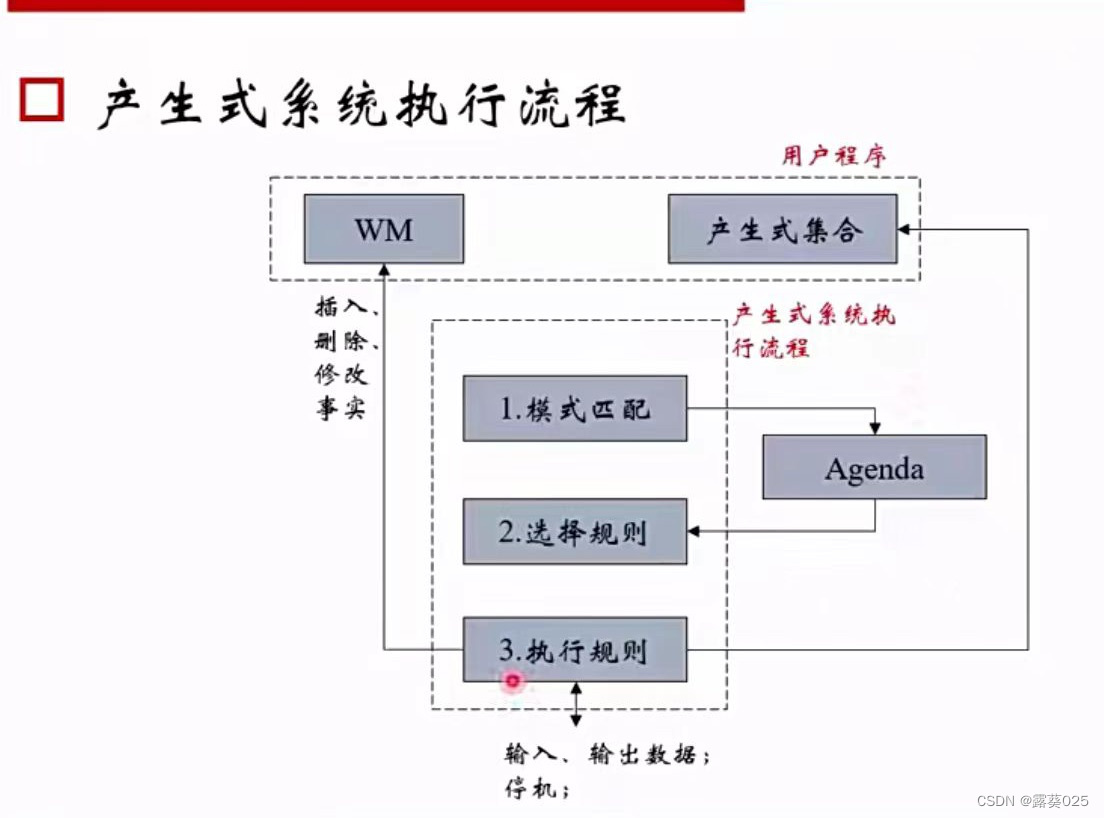
4.基于产生式规则的方法:
(1)产生式系统:
一种前向推理系统,可以按照一定机制执行规则,从而达到某些目标。常应用于自动规划,专家系统。
(2)产生式系统的组成:
事实集合,产生式/规则集合,推理引擎
(3)事实集/运行内存:
事实的集合,用于存储当前系统中所有事实
(4)事实(ABox):
描述对象:概念:属性:属性值
Student name:Alice
age:24
描述关系:
basicFact relation:oldThan
FirstArg:John
SecondArg:Alice
⬇️简
older Than John Alice
(5)产生式集合(类似于TBox)
产生式:IF condition THEN actions
condition:由条件组成的集合(LHS)

action:由动作组成的序列(RHS)

例如:
IF(Student name :x)
Then ADD(Person name:x)
如果有一个学生名为x,那么向事实集中加入一个事实,表示有一个名为x的人
(6)推理引擎
1).控制系统的执行
模式匹配(核心):用规则的条件部分匹配是事实集中的事实(WM),整个LHS都被满足的规则触发,并被加入议程(队列)。
(type x y),(subClassOf y z) ➡️ ADD(type x z)
x的type是y,y是z的子类 ➡️ 加一条x的tpe是z
(type Alice Ta) , (subClassOf Student Person)
(type Bob Ta) , (subClassOf Ta Student)
(type Mary Student)
⬇️融合join操作
(type Alice Ta) , (subClassOf Ta Student)
(type Bob Ta) , (subClassOf Ta Student)
(type Mary Student) , (subClassOf Student Person)
解决冲突:按一定的策略从被触发的多条规则中选择一条。
执行动作:执行被选择出来的规则的RHS,从而对WM进行一定的操作
产生式系统 = 事实集 + 产生式集合 + 推理引擎