Mysql实战-索引结构 二叉树/平衡二叉树/红黑树/BTree/B+Tree

我们在项目中都会使用索引，所以我们要了解索引的存储结构，今天我们就着重讲解下Mysql的索引结构存储模型，并且看下 二叉树，平衡二叉树，红黑树，BTree及B+Tree的演变过程

1.索引的组成

为什么会有索引？

为了方便我们查找数据，快捷的查找数据，就像目录一样，我们在翻书的时候，可以根据目录，直接找到相应的位置，在DB中，索引就是在读取的数据的过程中，查找数据的目录信息

什么是联合索引？

联合索引就是多个字段的索引， 为什么需要联合索引呢？ 下面我们看一个例子

user 表结构如下

CREATE TABLE `user` (
  `id` bigint NOT NULL AUTO_INCREMENT COMMENT '主键',
  `id_card` char(32) CHARACTER SET utf8mb4 COLLATE utf8mb4_unicode_ci NOT NULL COMMENT '身份证ID',
  `user_name` char(32) CHARACTER SET utf8mb4 COLLATE utf8mb4_unicode_ci NOT NULL COMMENT '用户名字',
  `age` int NOT NULL COMMENT '年龄',
  PRIMARY KEY (`id`)
) ENGINE=InnoDB AUTO_INCREMENT=1 DEFAULT CHARSET=utf8mb4 COLLATE=utf8mb4_unicode_ci COMMENT='用户表'

> OK
> 时间: 0.627s

如果我们需要查询 身份证号 和 姓名信息， 我们应该如何操作？

select user_name from user where id_card = "xxxxx"

这个查询语句意味着什么？ 回表查询

为什么会发生回表？这就要探究下我们的索引结构了，怎么能避免回表

2.索引结构

什么是回表查询 ？ 讲清楚 回表查询之前，我们必须清楚的知道 Mysql的索引存储结构，这样才能讲明白回表查询

大家都知道Mysql 采用B+Tree 来存储索引结构，那么你一定听说过BTree， 那么他们俩到底有什么区别呢？

• Btree 是为了磁盘或其他存储设备而设计的一种多叉平衡树
• Btree 相当于二叉树，Btree每个内节点有多个分支，即多叉
• B+Tree是BTree的一个变种，是BTree在数据库中的一个实现，是常见的也是数据库中使用最为频繁的一种索引

2.1 二叉树，二叉平衡树

二叉树是什么？

这是二叉树大致的情况

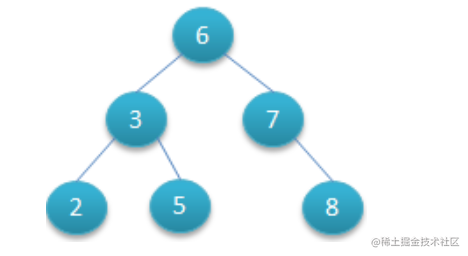
二叉树的极端情况-单链到底
二叉树 存在一种极端的情况， 这种效率就很差，一条链路走到底，效率极为低下

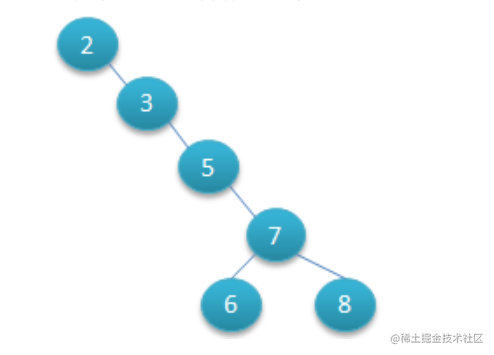
二叉平衡树
为了解决 一条路走到底的问题， 印出来了二叉平衡树，平衡二叉树 (AVL) 树是一种自平衡二叉查找树 (BST)，

• 平衡二叉树是二叉树对于空间密度提升的升级
• 平衡二叉树比二叉树比较有规则，所以深度比二叉树小
• 所有节点的左右子树的高度差不能超过 1
• 平衡二叉树在数据量大的时候查询和插入速度都大于二叉树

2.2 红黑树

那什么是红黑树呢？ 其实红黑树和上面的平衡二叉树类似， 红黑树是一种自平衡二叉搜索树

• 红黑树 每个节点多了一个额外的位置用来存储节点的颜色（红色或黑色）
• 每个节点颜色只有红或黑，要么是红色，要么是黑色，唯一选择
• 红黑树的根节点一定是黑色的
• 红黑树所有的叶子节点全是null，黑色
• 红黑树不能有相邻的红色节点，即红色节点不能有父/子 红节点
• 从任一节点到子树的每个叶子节点黑色节点数相同 叫做节点的黑高
• 从根节点到每个叶子节点路径的黑色节点数相同 叫做树的黑高

上面这些限制就是为了 红黑树实现自平衡而定义的准则，有了这些准则，就能避免 二叉树极端情况成为单链的场景，最后两点比较难理解，我们来验证下

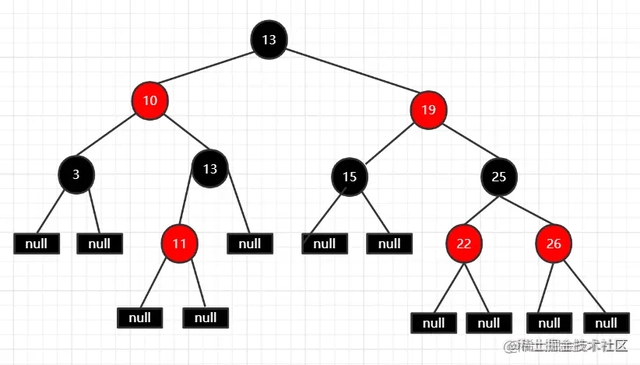
1. 从任一节点到子树的每个叶子节点黑色节点数相同 叫做节点的黑高
   • 计算节点黑高
   • 根13->叶子A， 13->3->null 节点黑高3
   • 根13->叶子B，13->19->25->26->null， 黑色节点 13，25，null 节点黑高3
   • 所以从任一节点到叶子节点 黑节点数相同，黑高
2. 从根节点到每个叶子节点路径的黑色节点数相同 叫做树的黑高
   • 根节点 13，到叶子A， 3个黑色节点， 树的黑高就是3
   • 黑高为3的红黑树，最小高度是3，全黑
   • 黑高为3的红黑树，最大高度是5，交替红黑
   • 黑稿为3的红黑树，子树最小高度是2，最大高度为4
     

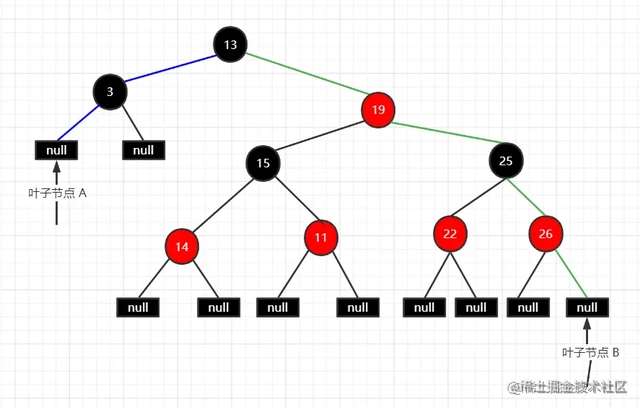
红黑树有什么操作呢？

红黑树的基本操作和其他树形结构一样，一般都包括查找、插入、删除等操作。

• 查找 红黑树是二叉树的一种，查找过程和二叉查找树一样
• 插入 红黑树的插入很复杂，红黑树插入新节点后，需要进行调整，新插入的新节点一定是红色
  • 如果插入的节点是黑色，那么这个节点所在路径比其他路径多出一个黑色节点，这个调整起来会比较麻烦。
  • 如果插入的节点是红色，此时所有路径上的黑色节点数量不变，仅可能会出现两个连续的红色节点的情况，这种情况下，通过变色和旋转进行调整即可
• 删除 删除更为复杂，要确定待删除节点有几个孩子，还要找删除节点的前驱/后继节点等等，不做赘述

2.3 B-Tree就叫做BTree

不存在B减树， 要么是BTree 要么是B+Tree，不存在B减树这种叫法，B树是一种多路自平衡搜索树，它类似普通的二叉树，但是BTree 允许每个节点有更多的子节点,这是和二叉树最大的区别， 每个子节点存在多节点

下面我们来看下BTree的特点 以下以下

• 所有键值分布在整个树中
• 任何关键字出现且只出现在一个节点中
• 搜索有可能在非叶子节点结束
• 在关键字全集内做一次查找，性能近似于二分查找算法

BTree 的数据存在每个节点中，所以每个节点能够保存的索引值很少，所以存储大量数据时，树的层级会很高，这样就导致与磁盘的 IO 交互次数增多，查找数据的效率就变得很低，为什么这么说？

我们来模拟一下BTree查找过程
可以看到有磁盘块和P1/P2/P3指针信息， 比如我现在要查找 60 60元素存储在 磁盘块9 中

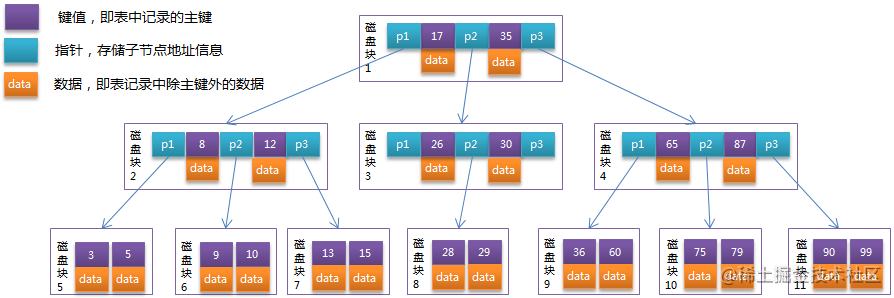
• 第一步 找 60 ， 先根据根节点信息，找到根节点存储的磁盘1 ，把磁盘1信息加载到内存 发生磁盘IO操作第1次
• 第二步 加载磁盘1后，内存中有两个文件17和35及3个记录其他磁盘的地址的指针数据P1/P2/P3，根据 60 >35 ,因此我们二叉树右子树查找，找到指针 P3
• 第三步 根据P3指针，定位磁盘4， 然后把磁盘4的信息加载到内存，发生磁盘IO操作第2次
• 第四步 加载磁盘4后，内存中有两个文件 65和87及3个记录其他磁盘的地址的指针数据P1/P2/P3，根据 60 < 65 ，因此我们找二叉树左子树查找，找到指针 P1
• 第五步 根据指针P1， 定位磁盘9， 然后把磁盘9的信息加载到内存，发生磁盘IO操作第3次
• 第六步 加载磁盘9后，内存中有两个文件 36和60， 对比 要找的元素 60，找到，并且定位了该文件所在的磁盘位置 磁盘9

该过程 发生了三次IO过程，从磁盘加载了3次数据信息， 频繁的从IO磁盘获取数据， 这就产生了B+Tree，下一篇文章，我们介绍下B+Tree

---

本文 我们介绍了索引的基本结构，包括二叉树，平衡二叉树，红黑树，BTree的演变过程和他们之间的区别，特别是红黑树，插入和删除都需要复杂的操作，也讲解了BTree的读取原理，继而引出B+Tree与之对比