503.下一个更大元素II

难点在于如何是实现数组的循环
但使用模拟遍历两次的时候注意始终使用index，别出现越界

class Solution {
public:
    vector<int> nextGreaterElements(vector<int>& nums) {
        stack<int> st;
        st.push(0);
        vector<int> res(nums.size(),-1);
        
        for(int i = 0; i < nums.size()*2;i++){
            int index = i % nums.size();
            while(!st.empty() && nums[index] > nums[st.top()]){
                res[st.top()] =  nums[index];
                st.pop();
            }
            st.push(index);
        }
        return res;
    }
};

42. 接雨水

本题首先要明确：按行统计还是按照列统计。
核心思想：按列统计，找到每一列左右两侧的最大值，取其中最小值，减去当前值就是这一列的雨水。其中第一根柱子和最后一根不做统计。
例如求列4的雨水高度：
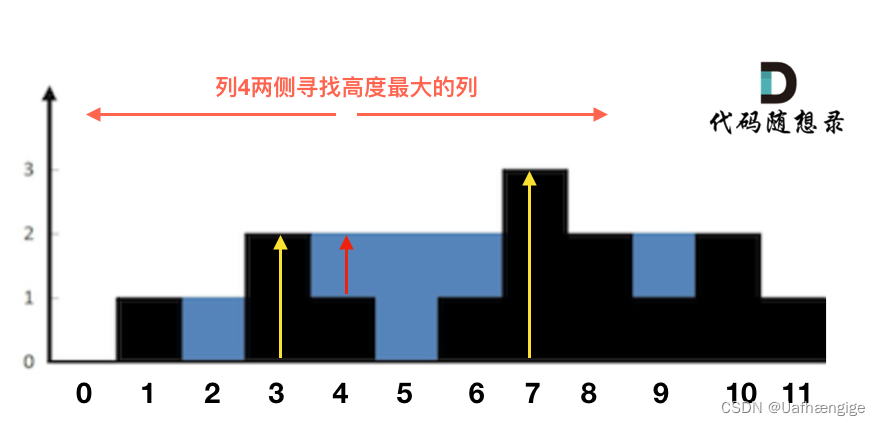列4 = min(2 , 3) - 1 = 1

1、暴力解法

那么暴力解法就是遍历数组，同时嵌套for寻找两边的最大值，这样时间复杂度就是O(n²)，超时

2、双指针优化
但其实没必要嵌套for数组，直接用数组遍历两边，每个列左边最大值记录在maxLeft数组，右边记录在maxRight数组就行。最后再遍历原始数组。

class Solution {
public:
    int trap(vector<int>& height) {
        vector<int> maxLeft(height.size(),0);
        vector<int> maxRight(height.size(),0);
        maxLeft[0] = height[0];
        for(int i = 1; i < height.size();++i){
            maxLeft[i] = max(height[i],maxLeft[i-1]);
        }
        maxRight[height.size()-1] = height[height.size()-1];
        for(int i = height.size()-2;i>=0;i--){
            maxRight[i] = max(maxRight[i+1],height[i]);
        }

        int sum = 0;
        for(int i = 1;i<height.size()-1;++i){
            int temp = min(maxLeft[i-1],maxRight[i+1]) - height[i];
            if(temp>0) sum+= temp;
        }
        return sum;
    }
};

3、单调栈解法
单调栈是按照行方向来计算雨水

一旦发现添加的柱子高度大于栈头元素了，此时就出现凹槽了，栈头元素就是凹槽底部的柱子，栈头第二个元素就是凹槽左边的柱子，而添加的元素就是凹槽右边的柱子。

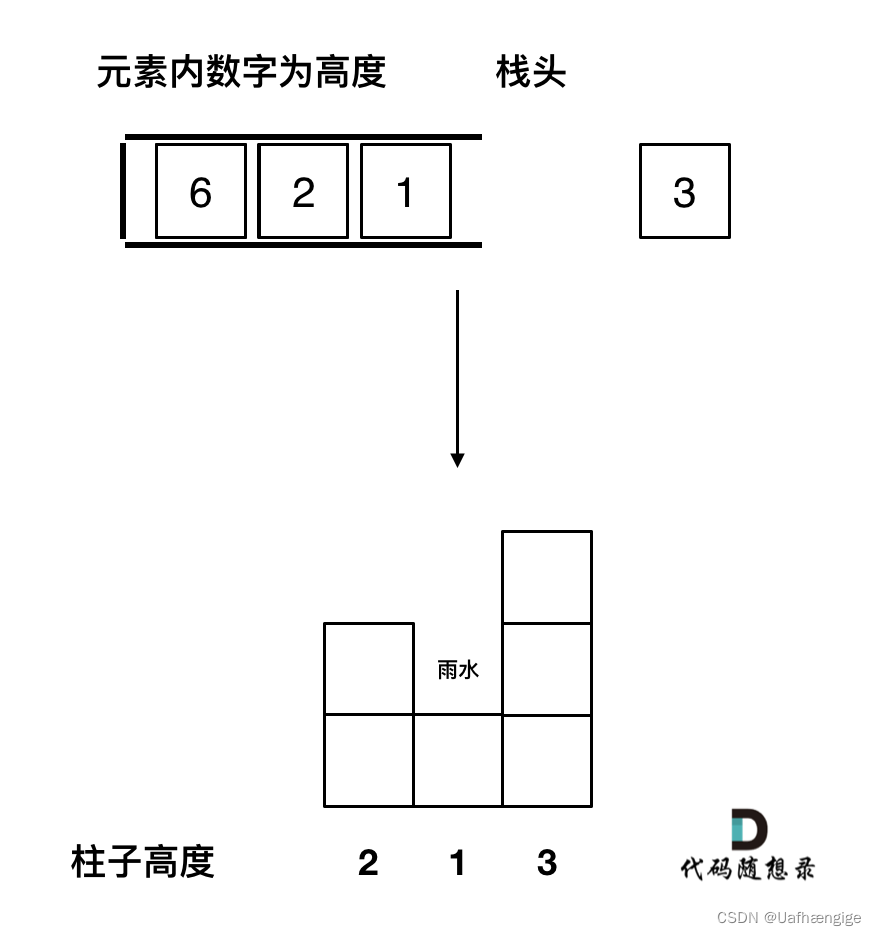
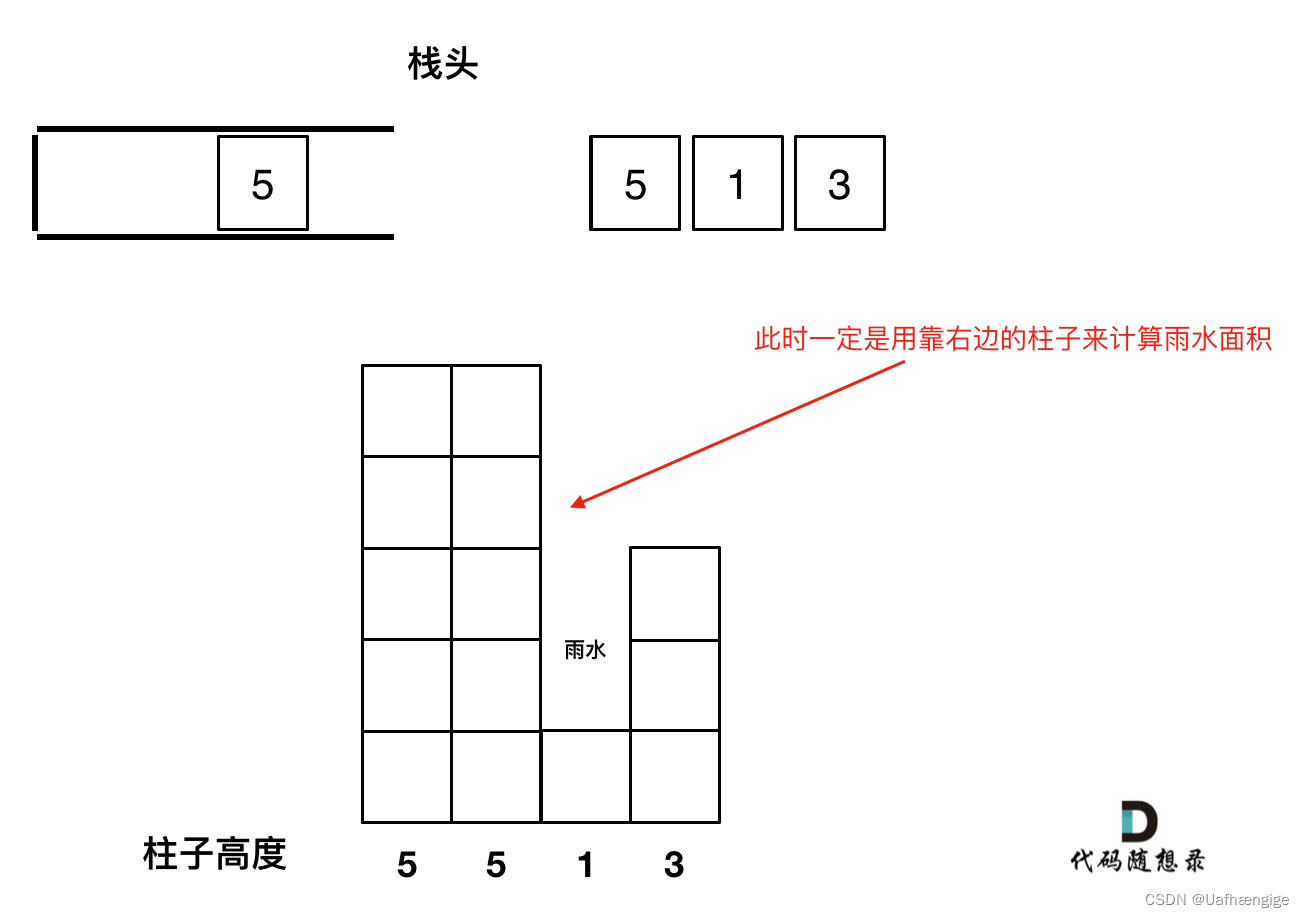
情况一：当前遍历的元素（柱子）高度小于栈顶元素的高度 height[i] < height[st.top()] 直接push
情况二：当前遍历的元素（柱子）高度等于栈顶元素的高度 height[i] == height[st.top()] 替换下标
情况三：当前遍历的元素（柱子）高度大于栈顶元素的高度 height[i] > height[st.top()] 利用左中右三个元素来求雨水

class Solution {
public:
    int trap(vector<int>& height) {
        stack<int> st;
        st.push(0);
        int sum = 0;
        for(int i = 1; i < height.size();++i){
            while(!st.empty() && height[i] > height[st.top()]){
                int mid = st.top();
                st.pop();
                if(!st.empty()){
                    int h = min(height[st.top()],height[i])-height[mid];
                    int w = i-st.top()-1;
                    sum += h*w;
                }
            }
            st.push(i);
        }
        return sum;
    }
};

84.柱状图中最大的矩形

跟接雨水相似，但是又不同。42. 接雨水 (opens new window)是找每个柱子左右两边第一个大于该柱子高度的柱子，而本题是找每个柱子左右两边第一个小于该柱子的柱子。
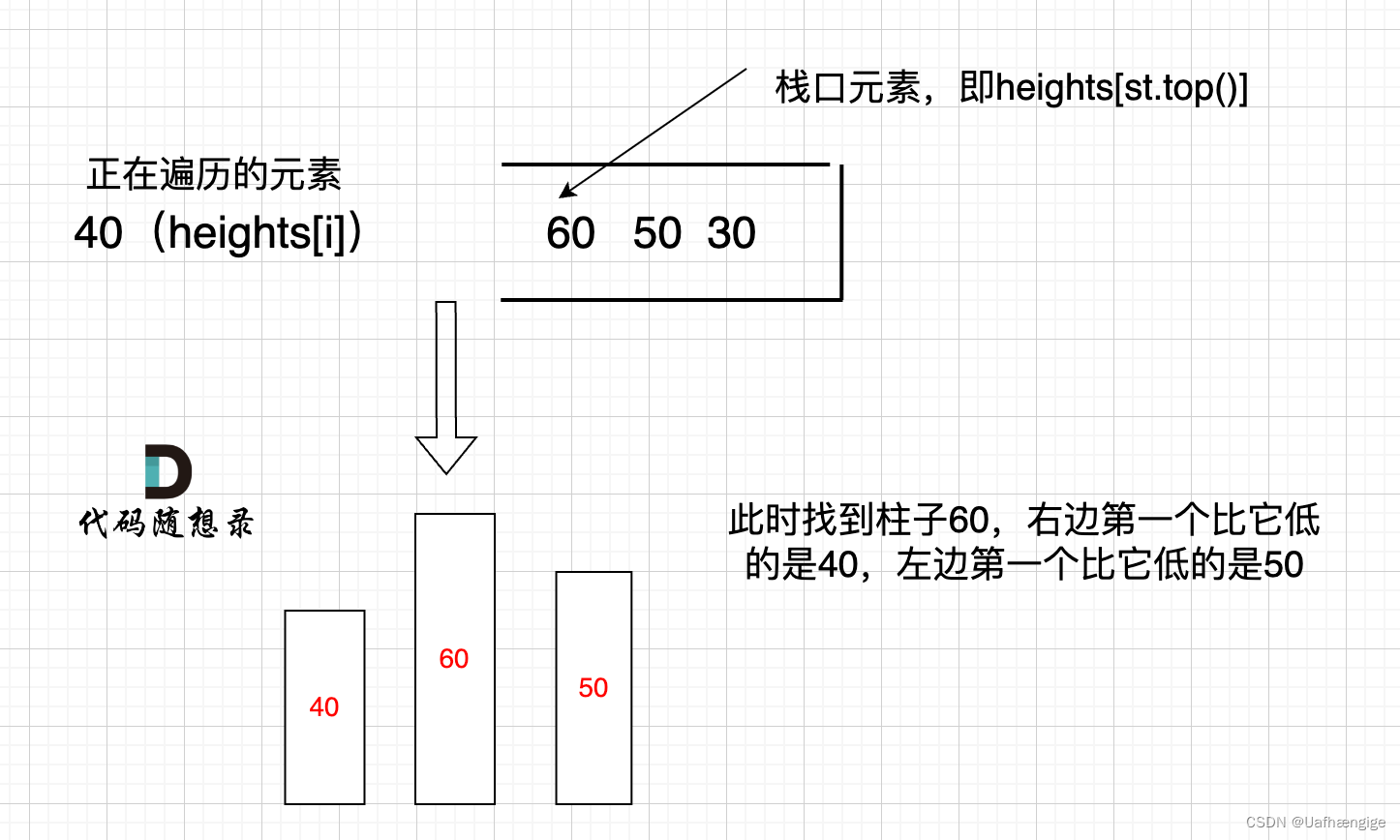只有栈里从大到小的顺序，才能保证栈顶元素找到左右两边第一个小于栈顶元素的柱子。

class Solution {
public:
    int largestRectangleArea(vector<int>& heights) {
        stack<int> st;
        heights.insert(heights.begin(), 0); // 数组头部加入元素0
        heights.push_back(0); // 数组尾部加入元素0
        st.push(0);
        int result = 0;
        for (int i = 1; i < heights.size(); i++) {
            while (heights[i] < heights[st.top()]) {
                int mid = st.top();
                st.pop();
                int w = i - st.top() - 1;
                int h = heights[mid];
                result = max(result, w * h);
            }
            st.push(i);
        }
        return result;
    }
};