ROC / AUC
- 1：坐标含义
- - （横坐标）FPR：伪阳性率，分类器 “分类错误的负样本个数” 占 “总负样本个数” 的比例。
  - （纵坐标）TPR：真阳性率，分类器 “分类正确的正样本个数” 占 “总正样本个数” 的比例。（召回率）
- 2：如何绘制roc曲线
- - 方法1：阈值法：更改阈值计算坐标点
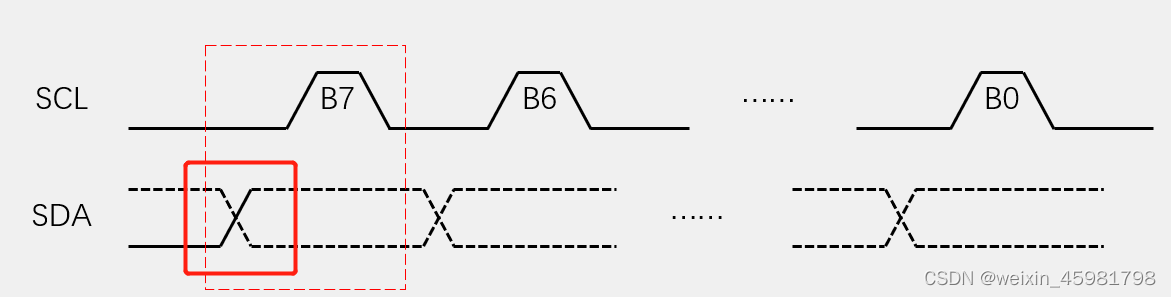
  - 方法2：折线法：遇到正负样本就画折线（样本概率从大到小排，经过一个正样本就向上，经过一个负样本就往右）
- 3：如何计算auc值
- - 方法1：根据定义（随机抽取样本对，正>负的概率）
  - 公式：[rank(正)累加 - m(m+1)/2] / m*n
  - - 分母：比如正M个，负N个，正负对为 M * N
    - 分子：正样本排名（从大到小）相加 - (1+2+...m-1)
    - 问题：两个样本概率值一样怎么办？（rank按照平均值处理）
    - 实现方法：
  - 方法2：按照图像面积累加（最后转化后跟公式版一样）
  - - 横面积：以负样本为阈值，每次为一格，每次就是1 / N
    - 纵面积：第一次大于负样本（第一个）为 a1/M 个，第二次大于负样本（第二个）为 a2/M 个。
    - 总面积：1 / N * a1/M + 1 / N * a2/M + .... = (a1+a2+... )/ M*N ; 分子为正大于负的总个数。
    - 总结：其实就是按照第二种画法去求的，将样本拍好序列，然后对于每个负样本为阈值，每过一次负样本就往横坐标去移动，然后横坐标的分割为1/N，纵坐标的高度即为每个负样本socre高的正样本的个数，即为正样本概率大于负样本概率的个数。
- 5：auc优点 / 缺点
- - 优点：
  - - a：AUC衡量的是一种排序能力，因此特别适合排序类业务；
    - b：AUC对正负样本均衡并不敏感，在样本不均衡的情况下，也可以做出合理的评估。其他指标比如precision，recall，F1，根据区分正负样本阈值的变化会有不同的结果，而AUC不需要手动设定阈值，是一种整体上的衡量方法。
  - 缺点：
  - - a：忽略了预测的概率值和模型的拟合程度；
    - b：AUC反应了太过笼统的信息。无法反应召回率、精确率等在实际业务中经常关心的指标；它没有给出模型误差的空间分布信息，AUC只关注正负样本之间的排序，并不关心正样本内部，或者负样本内部的排序，这样我们也无法衡量样本对于好坏客户的好坏程度的刻画能力；
- 6：采样对AUC的影响？
- - 问题：负采样在什么情况下提高auc ? 有些时候负采样提高不了auc。
- 7：auc衍生指标
- - 衍生1：总体计算没有反映个人（gauc）
  - - auc缺点：
    - - 1：不同用户，对比的个数不一样。造成影响不一样。
      - 2：无法体现不同用户真实的排序能力。
    - 如何计算GAUC：一般场景下权重为用户曝光的长度。
    - trick：
    - - 1：实际处理时可以尝试过滤掉单个用户全是正样本或负样本的情况。
      - 2：尽量不做batch的gauc指标，无法捕捉到用户的所有样本。
    - gauc其他场景的用处：
    - - 1：实数型目标时，转化为2分类，比如预测时长转为“有效播放”，“是否长播放”。
      - 2：在计算ctr的gauc时候，将权重调整为用户观看时长；计算cvr时候，转为用户消费金额。将重点反应模型对高价值用户群体的排序性能。
    - gauc代码实现：
- 8：你auc为啥这么高？过拟合了吧！论不平衡数据的评价指标选择
- - 现象：比如阈值0.5，label=1样本在0.7正太分布，如果100个正样本，那么在0.5以上有80个，召回率80%，准确率为XX，如果1000个正样本，那么在0.5以上有800个，召回率80%不变，但是准确率就会变大，因为正样本在所有样本中的比例变大。
  - 总结：不平衡比例在1:1到1:10的时候，如果你对正负样本的识别都比较看重，可以用用Accurate；在1:10到1:100之间的时候，可以用用AUC；极端不平衡时，分段统计P和R更加务实。
  - 衍生2：在广告场景中有缺陷（CPM-sensitive AUC）
- 问题：auc / PR 区别
- 问题：大数据量AUC怎么计算？
- - 方法1：采样
  - 方法2：[基于 PS-Lite 分布式计算 AUC](https://zhuanlan.zhihu.com/p/87339470)
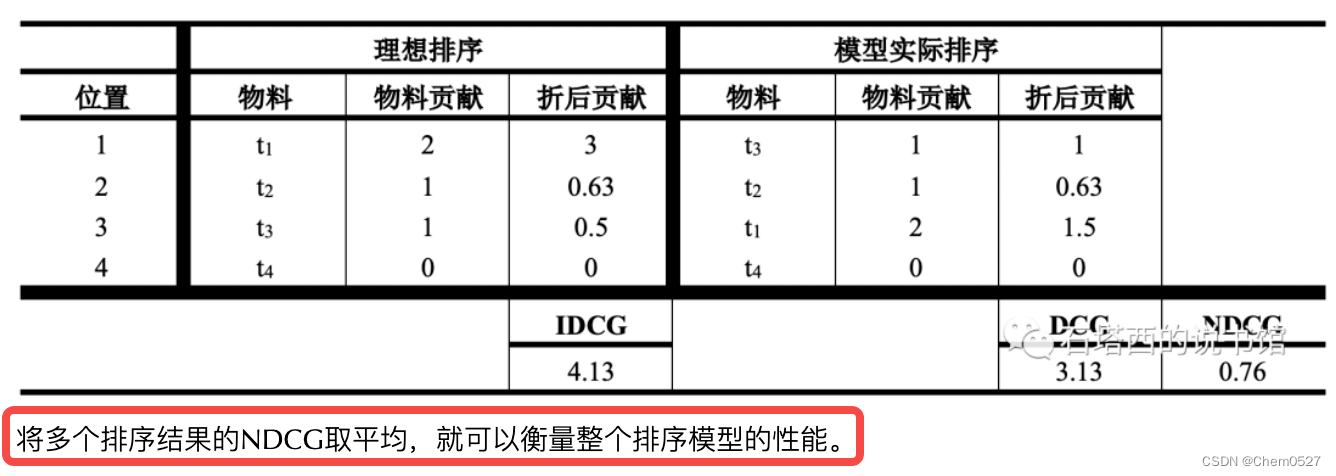
NDCG：考虑到每个位置上物料带来的收益和这个位置上的折扣效应。
- 解决的问题：排序越靠前越有可能被点击，auc不能反应这个“折扣”现象，比如[Plong,N1,Pshort,N2]，与[Pshort,N1,Plong,N2]，auc计算结果一样。
- DCG：
- IDCG：理论上完美的排序模型，按照物料的真实贡献度排名。
- 归一化 NDCG@K = DCG@K / IDDCG@K

ROC / AUC

看完这篇AUC文章，搞定任何有关AUC的面试不成问题~

随机挑选一个正样本和负样本，分类器将正样本排在负样本前面的概率。

使用AUC或者logloss可以避免把预测概率转换成类别。

1：坐标含义

（横坐标）FPR：伪阳性率，分类器 “分类错误的负样本个数” 占 “总负样本个数” 的比例。

（纵坐标）TPR：真阳性率，分类器 “分类正确的正样本个数” 占 “总正样本个数” 的比例。（召回率）

与基尼系数关系：gini+1 = 2*AUC
可以通过约登指数（TPR+1-FPR）取得最大时的阈值来确定一个分类器合适的阈值；

2：如何绘制roc曲线

方法1：阈值法：更改阈值计算坐标点

样本概率从大到小排，然后遍历每个样本进行设置阈值，分别计算横纵坐标，当我们将threshold设置为1和0时，分别可以得到ROC曲线上的(0,0)和(1,1)两个点。将这些(FPR,TPR)对连接起来，就得到了ROC曲线。当threshold取值越多，ROC曲线越平滑。（记好召回率大的时候就是阈值小的时候，把所有物品都判为正。）

方法2：折线法：遇到正负样本就画折线（样本概率从大到小排，经过一个正样本就向上，经过一个负样本就往右）

3：如何计算auc值

方法1：根据定义（随机抽取样本对，正>负的概率）

公式：[rank(正)累加 - m(m+1)/2] / m*n

分母：比如正M个，负N个，正负对为 M * N

分子：正样本排名（从大到小）相加 - (1+2+…m-1)

其实分子就是想计算出所有正比负大的组合数目，那么我们先按照score排序后，把所有正的score加起来，每个正的排名（99），就代表着这个正样本要比99个样本score大，但是里面包含了一部分正正情况(第一名正，包含了M-1种情况，第二名正包含了M-2种，最后一名正包含0种正正），所以将所有正的排名加起来再减去各自正正的个数，就是所有样本中正比负score大的个数。

手动版：
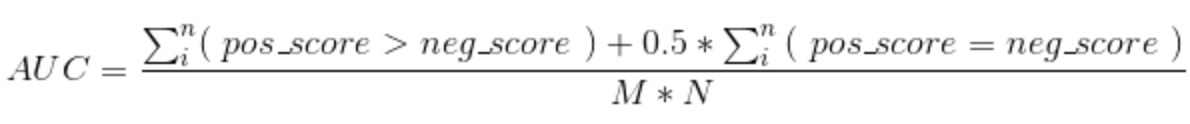
在这里插入图片描述
上式中，统计一下所有的 M×N(M为正类样本的数目，N为负类样本的数目)个正负样本对中，有多少个组中的正样本的score大于负样本的score。当二元组中正负样本的 score相等的时候，按照0.5计算。然后除以MN。

公式版：
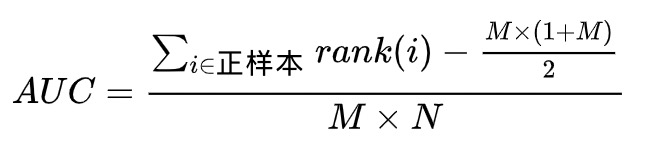
在这里插入图片描述

问题：两个样本概率值一样怎么办？（rank按照平均值处理）

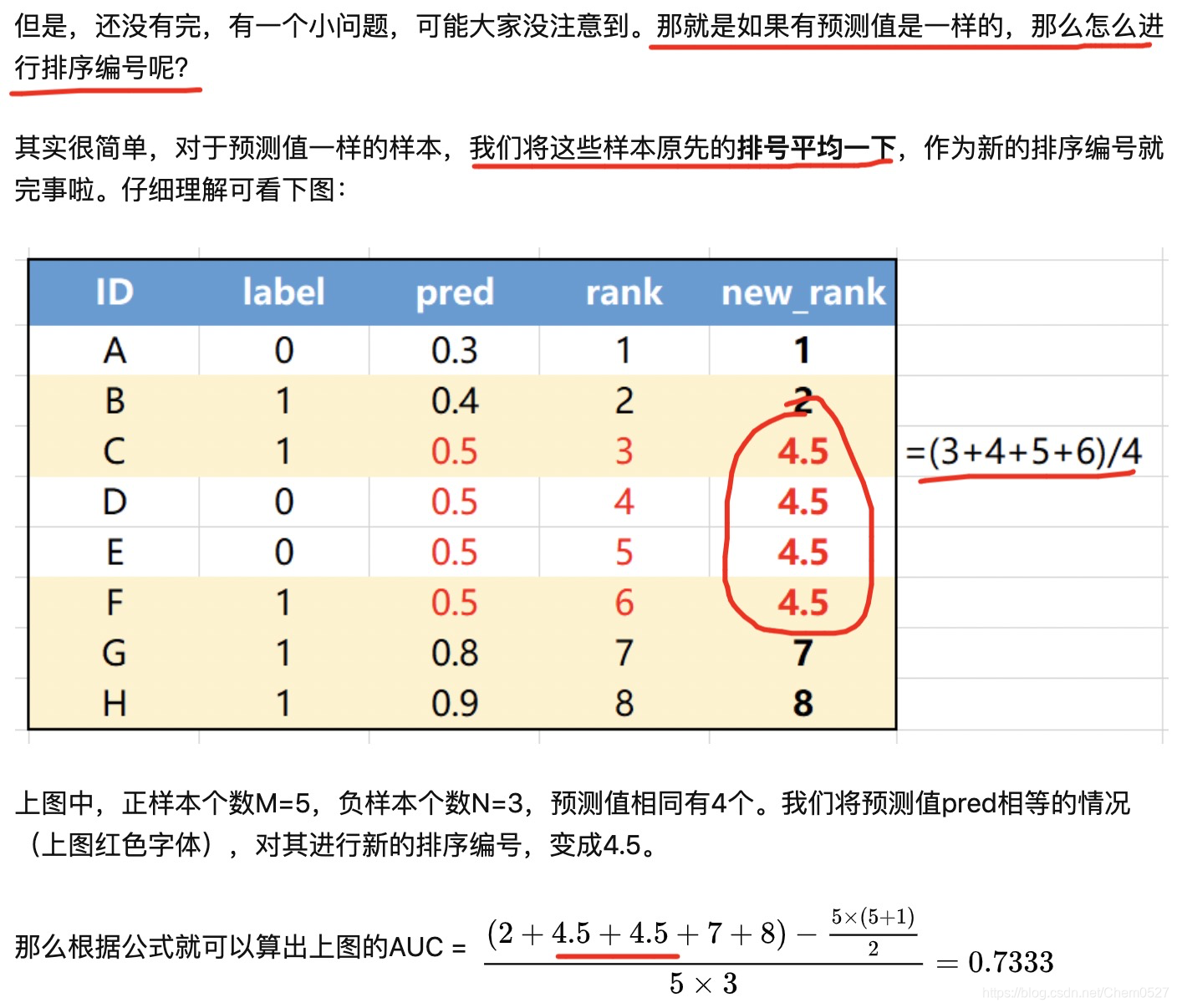
在这里插入图片描述

实现方法：

实现1：
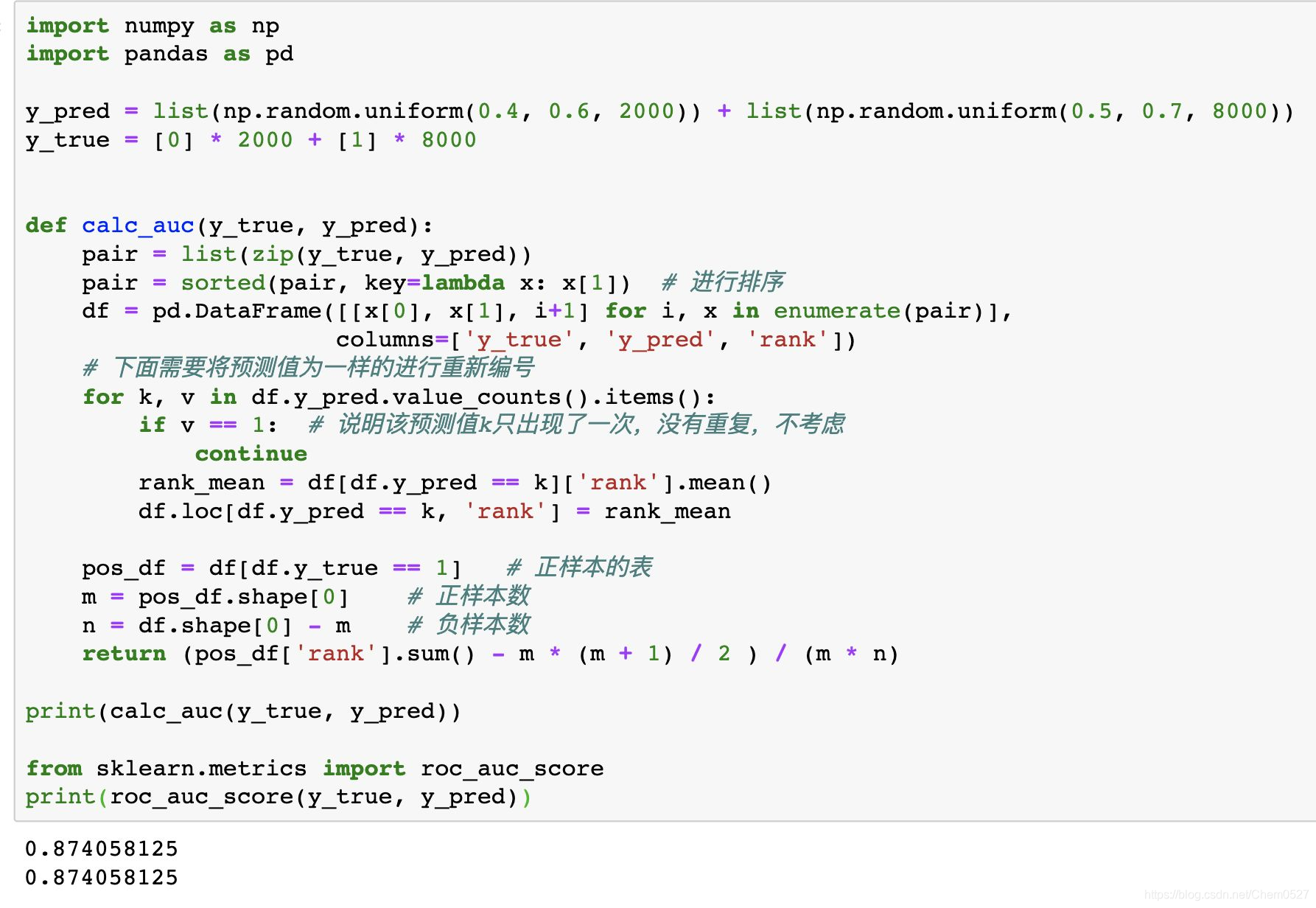
在这里插入图片描述
实现2：

def calAUC(prob,labels):
    """
    计算AUC主题逻辑
    :param prob:
    :param labels:
    :return:
    """

    # 组装预测值、标签，返回 List[(0.011547, 1), (0.00102014, 0), (0.000152839, 1)] 形式
    f = list(zip(prob, labels))
    # 以预测值为key进行排序，得到rank，记录了按照预测值排序后的label
    rank = [values2 for values1, values2 in sorted(f, key=lambda x:x[0])]
    # rankList记录了rank中正样本的位置（从1开始）
    rankList = [i+1 for i in range(len(rank)) if rank[i]==1]
    posNum = 0
    negNum = 0
    # 遍历label列表，查找正负样本数
    for i in range(len(labels)):
        if labels[i] == 1:
            posNum += 1
        else:
            negNum += 1
    auc = 0
    # 计算AUC, 计算公式 AUC = {正样本位置的和 - [正样本数*(正样本数+1)]/2} / 正样本数*负样本数
    auc = (sum(rankList) - (posNum*(posNum+1))/2)/(posNum*negNum)
    return auc


y = []
pred = []
with open("result_v1", 'r') as infile:
    for line in infile:
        pred.append(float(line.strip()))
with open("data/test_shuffle", 'r') as infile:
    for line in infile:
        y.append(int(line.strip().split(' ')[0]))

print(calAUC(pred,y))

实现3：

#!/usr/bin/env python
#-*- coding: utf-8 -*-
# ******************************************************************************
# 程序名称: roc_auc_score.py
# 功能描述: 计算roc曲线下方的面积
# 创建人名: aylanyang
# 创建日期: 2019-09-03
# 版本说明: v1.0
# ******************************************************************************

## import
import numpy as np
from sklearn.metrics import roc_auc_score, roc_curve
import matplotlib.pyplot as plt

def roc_auc_score_v1(prob, label):
    '''
    :param prob: 预测值
    :param label: 真实值
    :return: auc
    '''
    listTuple = list(zip(label, prob))
    rank = [values2 for values1, values2 in sorted(listTuple, key=lambda x: x[0])]
    rankList = [i+1 for i in range(len(rank)) if rank[i]==1]
    posNum = 0
    negNum = 0
    for i in range(len(label)):
        if(label[i] == 1):
            posNum += 1
        else:
            negNum += 1
    auc = (sum(rankList) - (posNum*(posNum+1))/2)/(posNum*negNum)
    return auc

def plot_roc(label, prob):
    fpr, tpr, _ = roc_curve(label, prob, pos_label=1)
    plt.figure()
    plt.plot(fpr, tpr, color='darkorange', lw=2, label='ROC Curve (Area = {:.2f}'.format(roc_auc_score(label, prob)))
    plt.plot([0, 1], [0, 1], color='navy', linestyle='--')
    plt.xlim([0, 1])
    plt.ylim([0, 1.05])
    plt.xlabel('False Positive Rate')
    plt.ylabel('True Postive Rate')
    plt.title('Receiver Operating Characteristic Curve')
    plt.legend(loc='lower right')
    plt.savefig('roc.png')
    plt.show()

if __name__ == "__main__":
    prob = np.array([0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9])
    label = np.array([0, 0, 0, 1, 0, 1, 1, 0, 1])
    auc = roc_auc_score_v1(label, prob)
    print('roc auc score: {:.4f}'.format(auc))
    auc = roc_auc_score(label, prob)
    print('roc auc score: {:.4f}'.format(auc))
    plot_roc(label, prob)

实现4：

import numpy as np
import matplotlib.pyplot as plt


def get_roc(y_label, y_score):

    """

    :param y_label:
    :param y_score:
    :return:
    """
    assert len(y_label) == len(y_score)
    # invert sort y_pred
    score_indices = np.argsort(y_score, kind="mergesort")[::-1]
    y_prob = np.array(y_score)[score_indices]
    y_true = np.array(y_label)[score_indices]

    # ------------------get tps and fps at distinct value -------------------------
    # extract the indices associated with the distinct values
    distinct_value_indices = np.where(np.diff(y_prob))[0]
    threshold_idxs = np.r_[distinct_value_indices, y_true.size - 1]

    # accumulate the true positives with decreasing threshold
    tps = np.cumsum(y_true)[threshold_idxs]

    # computer false positive
    fps = threshold_idxs + 1 - tps
    # ------------------------------ computer tpr and fpr---------------------------
    # Add an extra threshold position
    # to make sure that the curve starts at (0, 0)
    tps = np.r_[0, tps]
    fps = np.r_[0, fps]
    if fps[-1] <= 0:
        fpr = np.repeat(np.nan, fps.shape)
    else:
        fpr = fps / fps[-1]
    if tps[-1] <= 0:
        tpr = np.repeat(np.nan, tps.shape)
    else:
        tpr = tps / tps[-1]
    # -------------------------------computer auc------------------------------------
    height = np.diff(fpr)
    bottom = np.convolve(tpr, v=[1, 1], mode='valid')
    auc = np.sum(height * bottom / 2)

    return tpr, fpr, auc


def roc_plot(tpr, fpr, auc):
    """

    :param tpr:
    :param fpr:
    :param auc:
    :return:
    """
    plt.figure(figsize=(12, 8))

    plt.plot(fpr, tpr, color='darkorange',
             lw=2, label='ROC curve (area = {:.4f})'.format(auc))
    plt.plot([0, 1], [0, 1], color='navy', lw=2, linestyle='--')
    plt.fill_between(fpr, tpr, color='C0', alpha=0.4, interpolate=True)
    plt.xlim([0.0, 1.0])
    plt.ylim([0.0, 1.05])
    plt.xlabel('False Positive Rate')
    plt.ylabel('True Positive Rate')
    plt.title('Receiver operating characteristic example')
    plt.legend(loc="upper left")
    plt.show()


def main():
    y_label = [1, 1, 1, 1, 1, 0, 1, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 0, 1, 0]

    y_score = [-0.20079125, 0.30423529, 0.2010557, 0.27523383, 0.42592946, -0.15043958,
               -0.08794977, -0.12733765, 0.22931154, -0.23913774, -0.0638661, -0.14958713,
               -0.04915145, 0.09898199, 0.05155884, -0.1142967, 0.16105883, 0.04871601,
               -0.08258422, -0.26105925]

    tpr, fpr, auc = get_roc(y_label, y_score)
    roc_plot(tpr, fpr, auc=auc)
    print('Done')


if __name__ == "__main__":
    main()

实现5 sql：

整体计算：

select
    (ry - 0.5*n1*(n1+1))/n0/n1 as auc
from(
    select
        sum(if(y=0, 1, 0)) as n0, --50
        sum(if(y=1, 1, 0)) as n1,--100
        sum(if(y=1, r, 0)) as ry --100
    from(
        select y, row_number() over(order by score asc) as r
        from(
            select label as y, score
            from table.name
        )A
    )B
)C

分场景计算：

select
    scene,(ry - 0.5*n1*(n1+1))/n0/n1 as auc
from(
    select scene,
        sum(if(y=0, 1, 0)) as n0, --50
        sum(if(y=1, 1, 0)) as n1,--100
        sum(if(y=1, r, 0)) as ry --100
    from(
        select scene,y, row_number() over(partition by scene order by score asc) as r
        from(
            select scene,label as y, score
            from table.name
        )A
    )B group by scene
)C

用SQL计算AUC的三种方法

方法2：按照图像面积累加（最后转化后跟公式版一样）

横面积：以负样本为阈值，每次为一格，每次就是1 / N

纵面积：第一次大于负样本（第一个）为 a1/M 个，第二次大于负样本（第二个）为 a2/M 个。

总面积：1 / N * a1/M + 1 / N * a2/M + … = (a1+a2+… )/ M*N ; 分子为正大于负的总个数。

在这里插入图片描述
参考：LTR那点事—AUC及其与线上点击率的关联详解

总结：其实就是按照第二种画法去求的，将样本拍好序列，然后对于每个负样本为阈值，每过一次负样本就往横坐标去移动，然后横坐标的分割为1/N，纵坐标的高度即为每个负样本socre高的正样本的个数，即为正样本概率大于负样本概率的个数。

5：auc优点 / 缺点

优点：

a：AUC衡量的是一种排序能力，因此特别适合排序类业务；

b：AUC对正负样本均衡并不敏感，在样本不均衡的情况下，也可以做出合理的评估。其他指标比如precision，recall，F1，根据区分正负样本阈值的变化会有不同的结果，而AUC不需要手动设定阈值，是一种整体上的衡量方法。

缺点：

a：忽略了预测的概率值和模型的拟合程度；

b：AUC反应了太过笼统的信息。无法反应召回率、精确率等在实际业务中经常关心的指标；它没有给出模型误差的空间分布信息，AUC只关注正负样本之间的排序，并不关心正样本内部，或者负样本内部的排序，这样我们也无法衡量样本对于好坏客户的好坏程度的刻画能力；

6：采样对AUC的影响？

问题：负采样在什么情况下提高auc ? 有些时候负采样提高不了auc。

在这里插入图片描述

7：auc衍生指标

衍生1：总体计算没有反映个人（gauc）

auc缺点：

1：不同用户，对比的个数不一样。造成影响不一样。

在这里插入图片描述

2：无法体现不同用户真实的排序能力。

在这里插入图片描述

如何计算GAUC：一般场景下权重为用户曝光的长度。

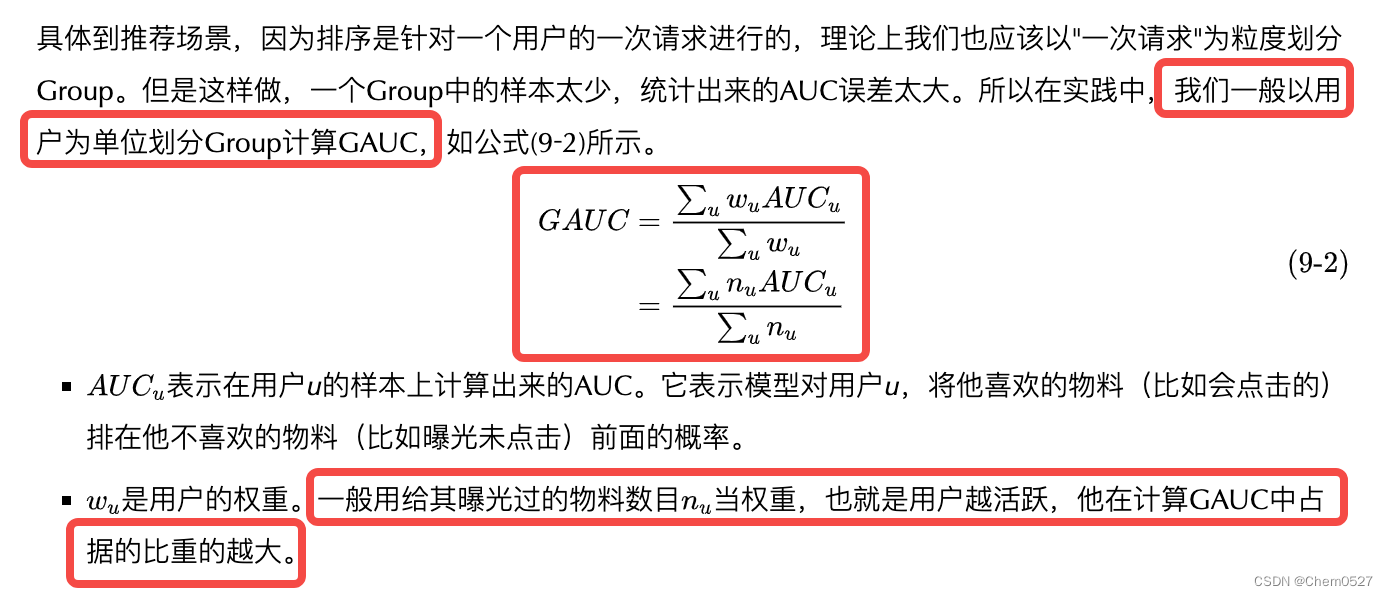
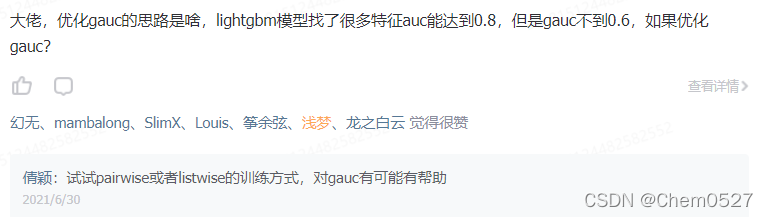
在这里插入图片描述

trick：

1：实际处理时可以尝试过滤掉单个用户全是正样本或负样本的情况。

在这里插入图片描述

2：尽量不做batch的gauc指标，无法捕捉到用户的所有样本。

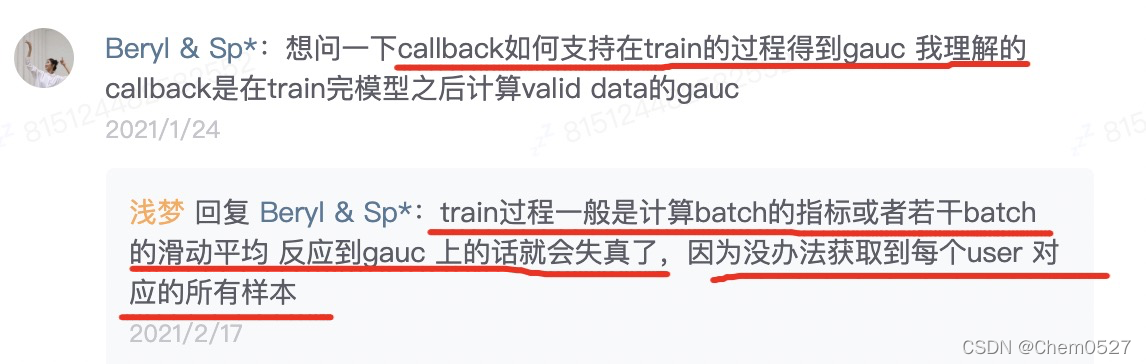
在这里插入图片描述

gauc其他场景的用处：

1：实数型目标时，转化为2分类，比如预测时长转为“有效播放”，“是否长播放”。

2：在计算ctr的gauc时候，将权重调整为用户观看时长；计算cvr时候，转为用户消费金额。将重点反应模型对高价值用户群体的排序性能。

在这里插入图片描述

gauc代码实现：

#!/usr/bin/env python
#-*- coding: utf-8 -*-
 
import numpy as np
from sklearn.metrics import roc_auc_score
from collections import defaultdict

def gauc(label, pred, user_id):
    '''
    :param label: ground truth
    :param prob: predicted prob
    :param user_id: user index
    :return: gauc
    '''
    if(len(label) != len(user_id)):
        raise ValueError("impression id num should equal to the sample num,"\
                         "impression id num is {}".format(len(user_id)))
    group_truth = defaultdict(lambda: [])
    group_score = defaultdict(lambda: [])
    for idx, truth in enumerate(label):
        uid = user_id[idx]
        group_truth[uid].append(label[idx])
        group_score[uid].append(pred[idx])
    group_flag = defaultdict(lambda: False)
    for uid in set(user_id):
        truths = group_truth[uid]
        for i in range(len(truths)-1):
            if(truths[i] != truths[i+1]):
                flag = True
                break
        group_flag[uid] = flag
    total_auc = 0
    total_impression = 0
    for uid in group_flag:
        if group_flag[uid]:
            total_auc += len(group_truth[uid]) * roc_auc_score(np.asarray(group_truth[uid]), np.asarray(group_score[uid]))
            total_impression += len(group_truth[uid])
    group_auc = float(total_auc) / total_impression
    group_auc = round(group_auc, 4)
    return group_auc

if __name__ == '__main__':
    user_id = ['a', 'a', 'a', 'b', 'b', 'b', 'a']
    label = [1, 0, 1, 0, 1, 1, 0]
    pred = [0.4, 0.5, 0.7, 0.2, 0.6, 0.7, 0.4]
    group_auc = gauc(label, pred, user_id)
    print('group_auc: {:.4f}'.format(group_auc))
    auc = roc_auc_score(label, pred)
    print("auc: {:.4f}".format(auc))

参考：推荐算法评价指标

8：你auc为啥这么高？过拟合了吧！论不平衡数据的评价指标选择

现象：比如阈值0.5，label=1样本在0.7正太分布，如果100个正样本，那么在0.5以上有80个，召回率80%，准确率为XX，如果1000个正样本，那么在0.5以上有800个，召回率80%不变，但是准确率就会变大，因为正样本在所有样本中的比例变大。

总结：不平衡比例在1:1到1:10的时候，如果你对正负样本的识别都比较看重，可以用用Accurate；在1:10到1:100之间的时候，可以用用AUC；极端不平衡时，分段统计P和R更加务实。

https://zhuanlan.zhihu.com/p/552278753

衍生2：在广告场景中有缺陷（CPM-sensitive AUC）

但是在广告排序场景下，线上排序通常考虑收益最大化，通过CTR * Bid进行排序，而非仅仅通过CTR进行排序。如果线下仅仅通过AUC来评价离线模型的效果，你往往会发现，线下的AUC涨了，但是线上的收入eCPM（千次广告展示收入）却降了。这是因为线下AUC的评估仅考虑点击率CTR，而线上展示不仅考虑了CTR，同时考虑了广告主的出价BID，二者之间存在一定的gap。

csAUC中，样本的排序是多层次的，负例是的level是最低的（lowest），而正例会按照其对应的bid进行排序，正例的bid越高，其level也是越高的。

参考：RS Meet DL(75)-考虑CPM的评估方法csAUC

问题：auc / PR 区别

P-R曲线及与ROC曲线区别

PR曲线会随着正负样本比例的变化而变化；但是ROC曲线不会。

从公式(2)和表中可以看出，TPR考虑的是第一行，实际都是正例，FPR考虑的是第二行，实际都是负例。因此，在正负样本数量不均衡的时候，比如负样本的数量增加到原来的10倍，那TPR不受影响，FPR的各项也是成比例的增加，并不会有太大的变化。因此，在样本不均衡的情况下，同样ROC曲线仍然能较好地评价分类器的性能，这是ROC的一个优良特性，也是为什么一般ROC曲线使用更多的原因。
即假设采样是随机的，采样完成后，给定一条正样本，模型预测为score1，由于采样随机，则大于score1的负样本和小于score1的负样本的比例不会发生变化。
但如果采样不是均匀的，比如采用word2vec的negative sample，其负样本更偏向于从热门样本中采样，则会发现auc值发生剧烈变化。
在这里插入图片描述