算法设计期末考试
- 1.分治法3选1
- 1.1全排列
- 1.2二分法--金块问题
- 1.3子数组换位问题
- 2.贪心选2题
- 2.1 活动安排
- 2.2 活动安排(改)
- 2.3 最优装载
- 2.4 多机调度
- 2.5 最优服务次序问题
- 2.6 多处最优服务次序问题
- 3.动态规划选1-2题
- 3.1最长公共子序列
- 3.2最大子段和
- 3.3 01背包问题
- 3.4 01背包问题--加入体积
- 4.回溯法1-2题
- 4.1 最优装载
- 4.2 01背包回溯法
- 4.3 批处理作业调度
- 4.4 n后问题
1.分治法3选1
1.1全排列
从n个不同元素中任取m(m≤n)个元素,按照一定的顺序排列起来,叫做从n个不同元素中取出m个元素的一个排列。当m=n时所有的排列情况叫全排列。
#include <iostream>
using namespace std;
const int MAX=2e5+7;
int result[MAX];
//下面是手工模拟了下第一趟的过程
//初始:i=1 k=1 m=4 1234
//prm(1,m):k=1 i=1 11交换 1234
//perm(2,m):k=2 i=2 22交换 1234
//perm(3,m):k=3 i=3 33交换 1234
//perm(4,m) k=4 结束 输出 1234
//33交换恢复 1234
//perm(3,m):k=3 i=4 34交换 1243
//perm(4,m) 结束 输出 1243
//34交换恢复 1234
//22交换恢复 1234
//perm(2,m):k=2 i=3 23交换 1324
// 33交换 1324
//输出结果 1324
//33交换恢复1324
//34 交换 1342
//输出结果 1342
// 34 交换 1324
//23交换恢复 1234
//perm(2,m):k=2 i=4 24交换 1432
//33
//输出
//33恢复
//34
//输出
//34恢复
//24交换恢复
//12交换 第2次循环开始
void swap(int a,int b){
int temp=result[a];
result[a]=result[b];
result[b]=temp;
}
void perm(int k,int m){
if(k==m){
//全排列结束
for(int i=1;i<=m;i++){
cout<<result[i]<<" ";
}
cout<<endl;
}
else{
for(int i=k;i<=m;i++){
if(i!=k) swap(i,k);//数组i和k位置元素互换
perm(k+1,m);
if(i!=k) swap(i,k);
}
}
}
int main(){
int m;
cin>>m;
for(int i=1;i<=m;i++){
result[i]=i;
}
perm(1,m);
return 0;
}
1.2二分法–金块问题
老板有一袋金块。每个月将有两名雇员会因其优异的表现分别被奖励一个金块。按规矩,排名第一的雇员将得到袋中最重的金块,排名第二的雇员将得到袋中最轻的金块。
#include <iostream>
using namespace std;
const int MAX=2e5+7;
float gold[MAX];
int Max_gold(int left,int right){
//如果只有一个金块,则这个金块为最大的
if(left==right) return gold[right];
//如果有2个金块,比较一下选出最大的
if(right-left==1) return (gold[right]> gold[left]? gold[right]:gold[left]);
//分治
int mid=(left+right)/2;
int max1=Max_gold(left,mid);
int max2=Max_gold(mid,right);
return max1>max2? max1:max2;
}
//下面同理
int Min_gold(int left,int right){
//如果只有一个金块,则这个金块为最小的
if(left==right) return gold[right];
//如果有2个金块,比较一下选出最大的
if(right-left==1) return (gold[right]> gold[left]? gold[left]:gold[right]);
//分治
int mid=(left+right)/2;
int min1=Min_gold(left,mid);
int min2=Min_gold(mid,right);
return min1<min2? min1:min2;
}
int main(){
int n;
cout<<"输入金块数目"<<endl;
cin>>n;
cout<<"输入各个金块重量"<<endl;
for(int i=0;i<n;i++){
cin>>gold[i];
}
cout<<Max_gold(0,n-1)<<endl<<Min_gold(0,n-1);
return 0;
}
1.3子数组换位问题
设a[0:n-1]是一个有n个元素的数组,k(0<=k<=n-1)是一个非负整数。
试设计一个算法将子数组a[0:k]与a[k+1,n-1]换位。要求算法在最坏情况下耗时O(n),且只用到O(1)的辅助空间。
当a[k]左边子数组的长度等于右边的子数组长度时,直接将两个子数组对应的元素互换即可
当左边子数组长度小于右边子数组长度时,将左边子数组与右边子数组右边的等长子数组对换,再对结果递归 调用对换函数
当右边子数组长度小于左边子数组长度时,将右边子数组与左边子数组左边的等长子数组对换,再对结果递归调用对换函数

#include <iostream>
using namespace std;
const int MAX=2e5+7;
float a[MAX];
//left:左边开始交换位置
//right:右边开始交换位置
void swap(int left,int right,int n){
int i=0,temp=0;
for(int i=0;i<n;i++){
temp=a[left+i];
a[left+i]=a[right+i];
a[right+i]=temp;
}
}
void patition(int k,int start,int end){
int n_left=k-start+1;
int n_right=end-k;
//左边子数组长度等于右边数组长度
if(n_left==n_right){
swap(start,start+n_left,n_left);
}
//左边子数组长度小于右边数组长度
else if(n_left<n_right){
swap(start,end-n_left+1,n_left);
patition(k,start,end-n_left);
}
//左边子数组长度大于右边数组长度
else{
swap(start,end-n_right+1,n_right);
patition(k,start+n_right,end);
}
}
int main(){
int n,k;
cout<<"输入n个数字"<<endl;
cin>>n;
for(int i=0;i<n;i++){
cin>>a[i];
}
cout<<"输入k"<<endl;
cin>>k;
//k==n-1时会发生数组地址越界,且k==n-1也不需要交换
if(k!=n-1){
patition(k,0,n-1);
}
for(int i=0;i<n;i++){
cout<<a[i];
}
return 0;
}
2.贪心选2题
2.1 活动安排
设有n个活动的集合E={1,2,…,n},其中每个活动都要求使用同一资源,如演讲会场等,而在同一时间内只有一个活动能使用这一资源。每个活动i都有一个要求使用该资源的起始时间si和一个结束时间fi,且si <fi。如果选择了活动i,则它在半开时间区间[si, fi)内占用资源。若区间[si, fi)与区间[sj, fj)不相交,则称活动i与活动j是相容的。也就是说,当si≥fj或sj≥fi时,活动i与活动j相容。活动安排问题就是要在所给的活动集合中选出最大的相容活动子集合。
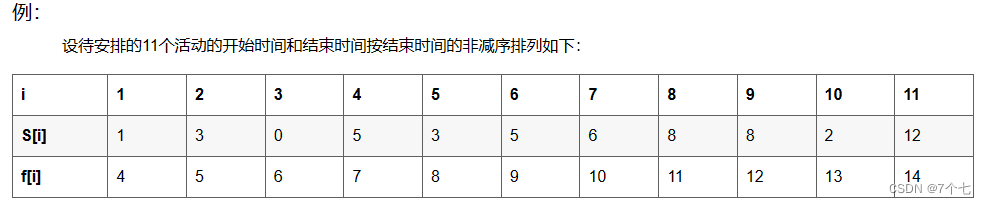
#include <iostream>
using namespace std;
int s[12]={0,1,3,0,5,3,5,6,8,8,2,12},f[12]={0,4,5,6,7,8,9,10,11,12,13,14};
int n=11;
bool flag[12];
int activitySelect(){
int count=1;
int last_fi=4;
flag[1]=true;
for(int i=2;i<=11;i++){
if(s[i]>=last_fi){
flag[i]=true;
last_fi=f[i];
count++;
}
}
return count;
}
int main(){
cout<<"活动序号:"<<endl;
for(int i=1;i<=11;i++)
cout<<i<<" ";
cout<<endl<<"活动开始时间:"<<endl;
for(int i=1;i<=11;i++)
cout<<s[i]<<" ";
cout<<endl<<"活动结束时间:"<<endl;
for(int i=1;i<=11;i++)
cout<<f[i]<<" ";
cout<<endl<<activitySelect()<<endl;
cout<<"选取的活动序号如下:"<<endl;
for(int i=1;i<=n;i++){
if(flag[i]) cout<<i<<" ";
}
return 0;
}
2.2 活动安排(改)

最少会场数 (按起始时间排序)
最多活动数 (按结束时间排序)
2.3 最优装载
#include<iostream>
#include<algorithm>
using namespace std;
const int MAXN=10000;
int main(){
int c,n; //c:船的最高载重量 n:物品数量
int sum=0,weight=0; //sum:装入的物品数量 weight:装入的物品重量
int w[MAXN]; //单个物品对应的重量
cout<<"请输入最高载重量和需载的物品数目:"<<endl;
cin>>c>>n;
cout<<"请分别输入这些物品的重量:"<<endl;
for(int i=1;i<=n;++i)
cin>>w[i];
sort(w+1,w+1+n);
for(int i = 1 ; i<=n ; i++){
weight += w[i]; //先将重量加进去
if(weight >= c){
if(weight == c) //恰好装满时
sum = i;
else
sum = i-1; //超重了,需要减去一个
break;
}
}
cout<<"最多可以装"<<sum<<"个"<<endl;
for(int i=1;i<=sum;i++)
cout<<w[i]<<" ";
return 0;
}
2.4 多机调度
设有n个独立的作业{1, 2, …, n},由m台相同的机器{M1, M2, …, Mm}进行加工处理,作业i所需的处理时间为ti(1≤i≤n),每个作业均可在任何一台机器上加工处理,但不可间断、拆分。多机调度问题要求给出一种作业调度方案,使所给的n个作业在尽可能短的时间内由m台机器加工处理完成。
贪心算法求解多机调度问题的贪心策略是最长处理时间的作业优先被处理
题目描述
有n台规格一样的机器同时工作,有m个零件需要加工,第i个零件加工时间为ti,请你计算出加工完这批零件最少需要多少时间。
输入
第一行为两个整数n,m。n表示机器数,m表示零件数(1<=n<=1e3,1<=m<=1e5)。
接下来一行m个整数为每个零件需要的加工时间(1<=ti<=1e3)。
输出
加工所有零件需要的最少时间。
样例输入
3 5
2 3 4 5 6
样例输出
7
#include <iostream>
#include <algorithm>
using namespace std;
const int MAX=10000;
int machine[MAX],job[MAX];
int findMachine(int m){
int min_idex=1;
for(int i=2;i<=m;i++){
if(machine[i]<machine[min_idex]){
min_idex=i;
}
}
return min_idex;
}
int Max(int m){
int max_idex=1;
for(int i=2;i<=m;i++){
if(machine[i]>machine[max_idex]){
max_idex=i;
}
}
return max_idex;
}
int main(){
int m,n;
cin>>m>>n;
//为了方便,所有数组下标都是从1开始
for(int i=1;i<=n;i++){
cin>>job[i];
}
//降序排序
sort(job+1,job+1+n,greater<int>());
//分配开始
for(int i=1;i<=n;i++){
//找出最先可以空闲的机器
int id=findMachine(m);
//分配任务
machine[id]=machine[id]+job[i];
//这题如果需要知道job序号,可以加一个映射jobToid
cout<<job[i]<<"分配给了机器"<<id<<endl;
}
//选出3个机器的最大的
cout<<machine[Max(m)];
}
2.5 最优服务次序问题


思路:短作业优先,平均等待时间最短
这题的平均等待时间是n个顾客等待直到完成服务的时间总和除以n
#include <iostream>
#include <cstdio>
#include <algorithm>
using namespace std;
const int MAX=10000;
int time[MAX];
int main(){
int n;
cout<<"n个乘客"<<endl;
cin>>n;
for(int i=1;i<=n;i++){
cin>>time[i];
}
//排序 10 20 30 40 10 + 10+20+ 10+20+30
sort(time+1,time+1+n,less<int>());
float sum=0;
//统计等待时间,正好time[0]=0
for(int i=1;i<=n;i++){
time[i]=time[i]+time[i-1];
sum=sum+time[i];
}
printf("%.2f",sum/n);
}
2.6 多处最优服务次序问题

对2.4进行修改就行
#include <iostream>
#include <algorithm>
#include <cstdio>
using namespace std;
const int MAX=10000;
int machine[MAX],t[MAX];
int findMachine(int m){
int min_idex=1;
for(int i=2;i<=m;i++){
if(machine[i]<machine[min_idex]){
min_idex=i;
}
}
return min_idex;
}
int main(){
int m,n,sum;
cin>>n>>m;
//为了方便,所有数组下标都是从1开始
for(int i=1;i<=n;i++){
cin>>t[i];
}
//升序排序
sort(t+1,t+1+n,less<int>());
//分配开始
for(int i=1;i<=n;i++){
//找出最先可以空闲的机器
int id=findMachine(m);
//分配任务
machine[id]=machine[id]+t[i];
//计算这个任务的等待时间
sum=sum+machine[id];
cout<<t[i]<<"分配给了机器"<<id<<endl;
}
printf("%.2f",1.0*sum/n);
}
3.动态规划选1-2题
3.1最长公共子序列
#include <bits/stdc++.h>
using namespace std;
void LCSlength(int m,int n,string x,string y,int c[][100],int b[][100]){
int i,j;
//初始化 ,c[i][j]记录Xi和yi序列最长公共子序列长度
//b用来记录
for(i=0;i<=m;i++){
c[i][0]=0;
}
for(i=0;i<=n;i++){
c[0][i]=0;
}
//打表
for(i=1;i<=m;i++){
for(j=1;j<=n;j++){
if(x[i]==y[j])
{
c[i][j]=c[i-1][j-1]+1; //当两序列最后一个相等
b[i][j]=1;
}
else if(c[i-1][j]>=c[i][j-1])
{
c[i][j]=c[i-1][j];
b[i][j]=2;
}
else
{
c[i][j]=c[i][j-1];
b[i][j]=3;
}
}
}
}
void LCS(int i,int j,string x,int b[][100]){
if(i==0||j==0){
return;
}
if(b[i][j]==1){
LCS(i-1,j-1,x,b);
cout<<x[i];
}
else if(b[i][j]==2){
LCS(i-1,j,x,b);
}
else if(b[i][j]==3){
LCS(i,j-1,x,b);
}
}
int main(){
string x;
string y;
cin>>x>>y;
//下面这2步是想让下标从1开始
x.insert(0,"1");
y.insert(0,"2");
int c[100][100];
int b[100][100];
int m=x.size()-1,n=y.size()-1;
LCSlength(m,n,x,y,c,b);
LCS(m,n,x,b);
return 0;
}
3.2最大子段和
#include <bits/stdc++.h>
using namespace std;
int ViolentMax(vector<int> a);
int f(vector<int> a,int l,int r);
int MaxSum(vector<int> a,int l,int r);
int MaxSum2(vector<int> a);
const int MAXN=2e5+7;
int dp[MAXN];
int main(){
vector<int> a;
int n;
cout<<"输入个数n" <<endl;
cin>>n;
cout<<"输入数字"<<endl;
int temp=0;
for(int i=1;i<=n;i++){
cin>>temp;
a.push_back(temp);
}
// cout<<ViolentMax(a);
// cout<<MaxSum(a,0,int(a.size()-1));
cout<<MaxSum2(a);
return 0;
}
//法一:暴力
int ViolentMax(vector<int> a){
int n=a.size(),sum=0,besti=0,bestj=0;
for(int i=0;i<n;i++){
int thisum=0;
for(int j=i;j<n;j++){
thisum+=a[j];
if(thisum>sum){
sum=thisum;
besti=i;
bestj=j;
}
}
}
cout<<besti<<endl<<bestj<<endl;
return sum;
}
//法二:分治算法
int MaxSum(vector<int> a,int l,int r){
if(l==r){
return a[l];
}
else{
int m=(l+r)/2;
int L=MaxSum(a,l,m);
int R=MaxSum(a,m+1,r);
int LR=f(a,l,r);
return max(max(L,R),LR);
}
}
int f(vector<int> a,int l,int r){//横跨左右的最大子段和
int m=(l+r)/2;
int sumL=0,ansL=a[m];
int sumR=0,ansR=a[m+1];
for(int i=m;i>=l;i--){
sumL+=a[i];
ansL=max(ansL,sumL);
}
for(int i=m+1;i<=r;i++){
sumR+=a[i];
ansR=max(ansR,sumR);
}
return ansL+ansR;
}
//法三:动态规划
//例如 2 -4 3 -1 2 -4 3
//以2为结尾的最大字段和 ans1=2
//以-4为结尾的最大字段和 ans1为正数则要;为负数或者0不要 即ans2=ans1+-4=-2
//以3 为结尾的最大字段和 ans2不要 ans3=3
//以第n个数的最大字段和 取决于前n-1个数的最大字段和
//dp[i]=dp[i-1]>0?dp[i-1]+a[i]:a[i]
int MaxSum2(vector<int> a){
int ans=0;
dp[0]=a[0]=ans;
for(int i=1;i<=int(a.size()-1);i++){
dp[i]=dp[i-1]>0?dp[i-1]+a[i]:a[i];
ans=max(ans,dp[i]);
}
return ans;
}
3.3 01背包问题
#include <bits/stdc++.h>
using namespace std;
void findmax(int w[],int v[],int n,int c);
void findwhat(int i,int j,int w[],int v[]);
int dp[100][100];
int main()
{
int c,n;
cout<<"输入容量和物品个数"<<endl;
cin>>c>>n;
cout<<"输入每个物体的重量和价值"<<endl;
int w[n+1],v[n+1];
for(int i=1;i<=n;i++){
cin>>w[i]>>v[i];
}
findmax(w,v,n,c);
cout<<"最大价值:"<<dp[n][c]<<endl;
findwhat(n,c,w,v);
return 0;
}
//打表
void findmax(int w[],int v[],int n,int c){
//初始化
for(int i=0;i<=n;i++){
dp[i][0]=0;
}
for(int j=0;j<=c;j++){
dp[0][j]=0;
}
//dp[i][j]:装到第i个物品 用了j个容量的最优解
for(int i=1;i<=n;i++){
for(int j=1;j<=c;j++){
//若不能放此时的物品i,即j<w[i],则dp[i][j]=dp[i-1][j]
if(j<w[i]){
dp[i][j]=dp[i-1][j];
}
//若当前可以放入此时的物品i,即j>=w[i],则在装和不装选一个最大即为最优解
//装:dp[i][j]=dp[i-1][j-w[i]]+v[i] 不装:dp[i][j]=dp[i-1][j]
else dp[i][j]=max(dp[i-1][j-w[i]]+v[i],dp[i-1][j]);
}
}
}
//回朔
void findwhat(int i,int j,int w[],int v[]){
if(i>=0){
//说明没装当前的i
if(dp[i][j]==dp[i-1][j]){
findwhat(i-1,j,w,v);
}
else if(j-w[i]>=0&&dp[i][j]==dp[i-1][j-w[i]]+v[i]){
cout<<i<<endl;
findwhat(i-1,j-w[i],w,v);
}
}
}
3.4 01背包问题–加入体积

4.回溯法1-2题
4.1 最优装载
已知n个集装箱,轮船载重量为c,集装箱i的重量为Wi,要求是在不超重的情况下,装尽可能多数量的集装箱.
注意: 有两个轮船时,以下代码用于轮船1,而轮船2用于放置剩余的集装箱。
#include<iostream>
using namespace std;
int w[100];//存储货物重量
int x[100];//标记走过的路径
int bestx[100]; //用来记录最优路径
int n;//箱子数目
int cw;//当前重量
int bestw;//最优重量
int c[2];
int rw=0;
void backtrack (int i)
//最优装载方案:第一艘轮船尽量装满
{
if (i>n) {
if(cw>bestw)
{
for(int j=1;j<=n;j++)
bestx[j]=x[j];
bestw=cw;
return ;
}
} //叶子节点,输出结果
else{
rw-=w[i];
if (cw+w[i]<=c[0]){//如果容量足够
//装
cw+=w[i];
x[i]=1;
backtrack (i+1);
//恢复
x[i]=0;
cw-=w[i];
}
//如果不装时:当前集装箱加剩下来的所有的都没有之前的记录的最大值大,则不需要进入下一层了
if(cw+rw>bestw){
backtrack (i+1);
}
rw+=w[i];
}
}
int main(){
cout<<"2个集装箱容量";
cin>>c[0]>>c[1];
cout<<"输入货物数目";
cin>>n;
for(int i=1;i<=n;i++){
cin>>w[i];
rw+=w[i];
}
backtrack (1);
for(int i=1;i<=n;i++){
cout<<bestx[i]<<endl;
};
return 0;
}
4.2 01背包回溯法
和4.1一样的思路,进行修改就行。
#include<iostream>
using namespace std;
int w[100];//物品重量
int v[100];//物品价值
int x[100];//标记走过的路径
int bestx[100]; //用来记录最优路径
int n;//箱子数目
int cw;//当前重量
int cv;//当前价值
int bestw;//最优重量
int c;
int rv=0;
void backtrack (int i)
//最优装载方案:第一艘轮船尽量装满
{
if (i>n) {
if(cv>bestw)
{
for(int j=1;j<=n;j++)
bestx[j]=x[j];
bestw=cv;
return ;
}
} //叶子节点,输出结果
else{
rv-=v[i];
if (cw+w[i]<=c){//如果容量足够
//装
cw+=w[i];
cv+=v[i];
x[i]=1;
backtrack (i+1);
//恢复
x[i]=0;
cw-=w[i];
cv-=v[i];
}
//如果不装时:当前已装价值加剩下来的所有的价值数 都没有之前的记录的最大值大,则不需要进入下一层了
if(cv+rv>bestw){
backtrack (i+1);
}
rv+=v[i];
}
}
int main(){
cout<<"输入背包容量和输入物品数目"<<endl;
cin>>c>>n;
cout<<"输入物品的重量和价值"<<endl;
for(int i=1;i<=n;i++){
cin>>w[i]>>v[i];
rv+=v[i];
}
backtrack (1);
for(int i=1;i<=n;i++){
cout<<bestx[i]<<" ";
};
cout<<endl<<bestw;
return 0;
}
4.3 批处理作业调度
每一个作业Ji都有两项任务分别在2台机器上完成。每个作业必须先有机器1处理,然后再由机器2处理。作业Ji需要机器j的处理时间为tji。对于一个确定的作业调度,设Fji是作业i在机器j上完成处理时间。则所有作业在机器2上完成处理时间和f=F2i,称为该作业调度的完成时间和。
对于给定的n个作业,指定最佳作业调度方案,使其完成时间和达到最小。
区别于流水线调度问题:批处理作业调度旨在求出使其完成时间和达到最小的最佳调度序列;
流水线调度问题旨在求出使其最后一个作业的完成时间最小的最佳调度序列;
思路:
- 预处理:给x赋初值,即其中一种排列,如x=[1,3,2];M[x[j]][i]代表当前作业调度x排列中的第j个作业在第i台机器上的处理时间;如M[x[2]][1]就意味着作业3在机器1上的处理时间。
- 假定当前作业调度排列为:x=[1,2,3];f1[i]即第i个作业在机器1上的处理时间,f2[j]即第j个作业在机器2上的处理时间;则:
f1[1]=M[1][1] , f2[1]=f1[1]+M[1][2]
f1[2]=f1[1]+M[2][1] , f2[2]=MAX(f2[1],f1[2])+M[2][2] //f2[2]不光要等作业2自己在机器1上的处理时间,还要等作业1在机器2上的处理时间,选其大者。
f1[3]=f1[2]+M[3][1] , f2[3]=MAX(f2[2],f1[3])+M[3][2]
4.4 n后问题

#include<iostream>
#include<cmath>
using namespace std;
int x[100];//标记走过的路径
int n=0;
int sum=0;
bool place(int t){
bool flag=true;
for (int i = 1; i <t; i++) {//判断是否与已放置的皇后冲突,
if ( x[t] == x[i] || fabs(t - i) == fabs(x[t] - x[i])) {
flag = false;
break;
}
}
return flag;
}
void backtrack (int t)
{ //叶子节点,输出结果
if (t>n) {
for(int i=1;i<=n;i++){
cout<<x[i]<" ";
}
cout<<endl;
sum++;
}
else{
for(int i=1;i<=n;i++){
x[t]=i;
if(place(t)){
backtrack(t+1);
}
}
}
}
int main(){
cout<<"输入棋盘规模";
cin>>n;
//初始化
for(int i=1;i<=n;i++){
x[i]=0;
}
backtrack (1);
cout<<sum;
return 0;
}


![[Orillusion]-使用 -windwos-4行命令](https://img-blog.csdnimg.cn/56682b33d1474df980127fb763abf4cf.png)