【ONE·C++ || set和map（三）：基于红黑树的封装框架】

news2024/11/27 23:54:32

总言

  主要介绍map、set的封装框架。

文章目录

  • 总言
  • 1、基本框架说明
  • 2、map、set封装Ⅰ：用于比较的仿函数
  • 3、map、set封装Ⅱ：迭代器实现
    • 3.1、基本说明
    • 3.2、begin()、end()、operator*、operator&、operator==、operator!=
      • 3.2.1、begin()、end()
      • 3.2.2、operator*、operator&、operator==、operator!=
    • 3.3、operator++、operator- -
      • 3.3.1、operator++
      • 3.3.2、operator- -
    • 3.4、Insert满足pair<iterator,bool>返回值、operator[]
      • 3.4.1、Insert
      • 3.4.2、operator[]
  • 4、总览
    • 4.1、set
    • 4.2、map
    • 4.3、RedBlackTree

  
  
  

1、基本框架说明

  1）、问题说明与stl底层查看
  问题：map和set底层都是通过红黑树实现，但我们知道二者功能各不相同，比如map为Key·Value模型，而set为Key模型。如果通过红黑树实现，是否意味着我们需要分别实现两个功能类似的红黑树？
  
  我们来看看库里是如何实现的：


#ifndef __SGI_STL_SET_H
#define __SGI_STL_SET_H

#include <tree.h>
#include <stl_set.h>

#ifdef __STL_USE_NAMESPACES
using __STD::set;
#endif /* __STL_USE_NAMESPACES */

#endif /* __SGI_STL_SET_H */

#ifndef __SGI_STL_MAP_H
#define __SGI_STL_MAP_H

#include <tree.h>
#include <stl_map.h>

#ifdef __STL_USE_NAMESPACES
using __STD::map;
#endif /* __STL_USE_NAMESPACES */

#endif /* __SGI_STL_MAP_H */

  
  相关分析：
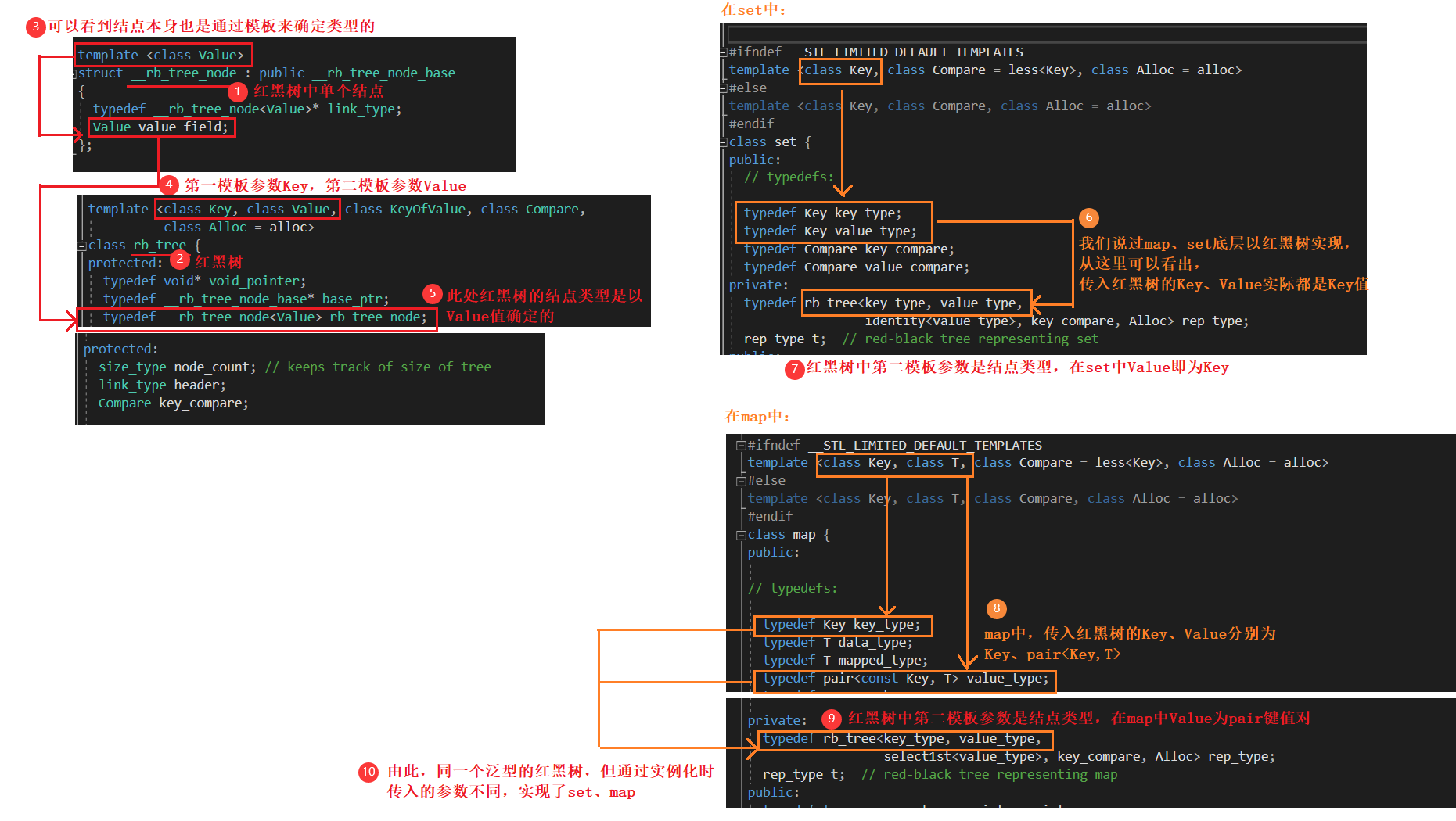
在这里插入图片描述
  
  
  
  2）、map、set中框架搭建
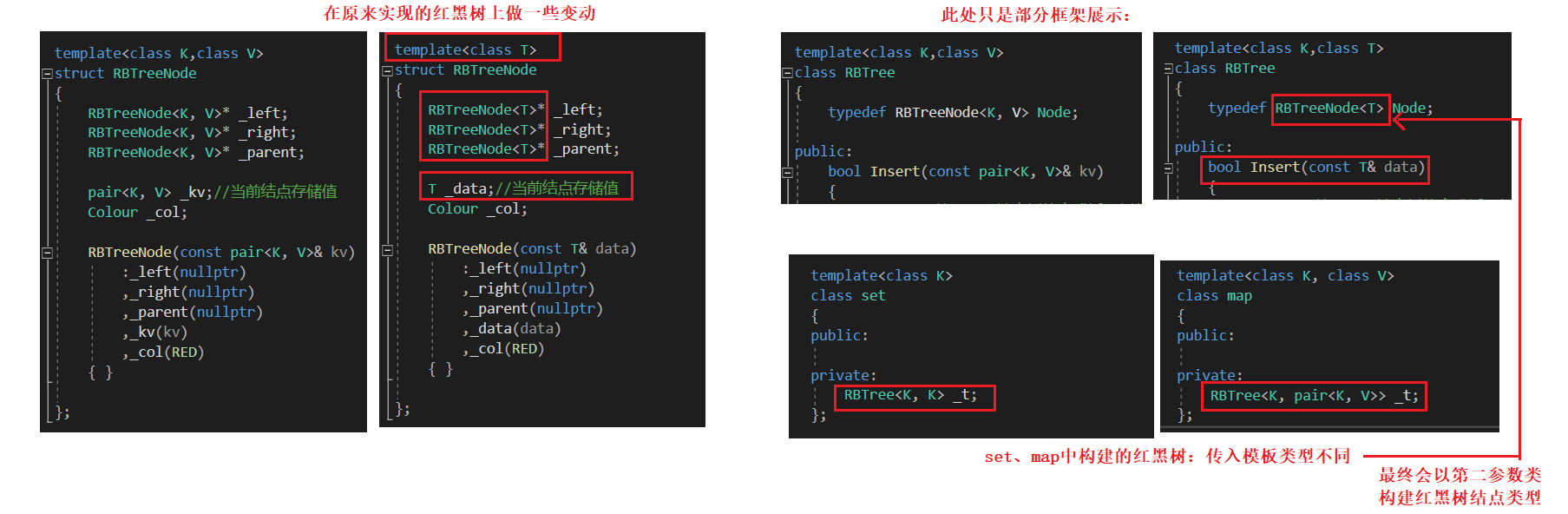
  根据上述分析，我们来对原先的红黑树做修改，相关框架：set和map（二）：AVL树和红黑树

在这里插入图片描述

template<class T>
struct RBTreeNode//红黑树结点
{
	RBTreeNode<T>* _left;
	RBTreeNode<T>* _right;
	RBTreeNode<T>* _parent;

	T _data;//当前结点存储值
	Colour _col;

	RBTreeNode(const T& data)
		:_left(nullptr)
		,_right(nullptr)
		,_parent(nullptr)
		,_data(data)
		,_col(RED)
	{ }

};


template<class K,class T>
struct RBTree //红黑树
{
	typedef RBTreeNode<T> Node;
	//……
private:
	Node* _root = nullptr;
};

namespace my_set
{
	template<class K>
	class set
	{
	public:
		//……
		//其它实现
		
	private:
		RBTree<K, K> _t;
	};
}

namespace my_map
{
	template<class K, class V>
	class map
	{
	public:
		//……
		//其它实现
		
	private:
		RBTree<K, pair<K, V>> _t;
	};
}

  
  问题说明:

  1、template<class K, class T> struct RBTree ：此处我们实现红黑树结点只需要第二参数T，那么第一参数K有何用？
  回答：比如find，我们要根据第一参数Key的值，找到对应的结点。
  
  
  

2、map、set封装Ⅰ：用于比较的仿函数

  1）、问题引入
  2、上述修改后存在的问题：比较。在原先红黑树中，我们实现了Insert，其判断结点位置时，直接通过运算符进行比较查询合适结点位置。

			if (cur->_data.first < data.first)
			{
				//……
			}
			else if (cur->_data.first > data.first)
			{
				//……
			}

  但这里RBTree是用于实现set、map。对于T _data;，二者一个结点类型为K，一个为pair<K,V>，但都要同时做到使用K(Key)值比较判断。如何做到？
  
  
  
  2）、相关实现
  方法说明：这里我们为set、map分别实现一个仿函数，根据其各自需求，返回我们需要的用于比较的值：
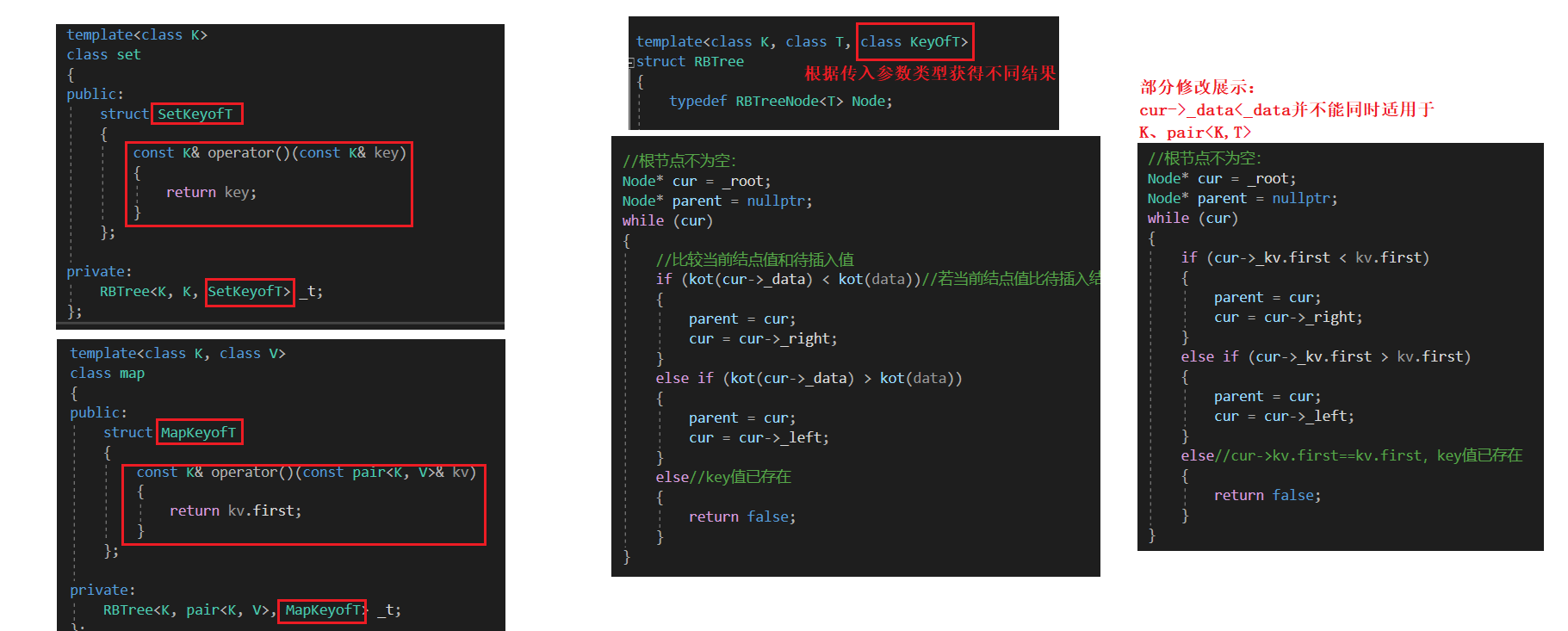
在这里插入图片描述

  
  在set中：

	template<class K>
	class set
	{
	public:
		struct SetKeyofT
		{
			const K& operator()(const K& key)
			{
				return key;
			}
		};

	private:
		RBTree<K, K, SetKeyofT> _t;
	};
}

  在map中：

	template<class K, class V>
	class map
	{
	public:
		struct MapKeyofT
		{
			const K& operator()(const pair<K, V>& kv)
			{
				return kv.first;
			}
		};

	private:
		RBTree<K, pair<K, V>, MapKeyofT> _t;
	};

  RBTree中，相关查找修改如下：

			KeyOfT kot;
			
			if (kot(cur->_data) < kot(data))//若当前结点值比待插入结点值小，说明待插入结点值在其右子树
			{
				//……
			}
			else if (kot(cur->_data) > kot(data))
			{
				//……
			}

  框架展示：我们增添了一个class KeyOfT，根据map、set传入的不同仿函数，获取不同结果。

template<class K, class T, class KeyOfT>
struct RBTree
{
	typedef RBTreeNode<T> Node;

public:
	bool Insert(const T& data)
	{
		KeyOfT kot;

		//step1：按照二叉搜索树的方式插入新节点
		Ⅰ、寻找位置
		if (_root == nullptr)//单独处理：根节点为空时
		{
			_root = new Node(data);
			_root->_col = BLACK;//根节点默认为黑色
			return true;
		}

		//根节点不为空：
		Node* cur = _root;
		Node* parent = nullptr;
		while (cur)
		{
			//比较当前结点值和待插入值
			if (kot(cur->_data) < kot(data))//若当前结点值比待插入结点值小，说明待插入结点值在其右子树
			{
				parent = cur;
				cur = cur->_right;
			}
			else if (kot(cur->_data) > kot(data))
			{
				parent = cur;
				cur = cur->_left;
			}
			else//key值已存在
			{
				return false;
			}
		}

		Ⅱ、插入值，调整链接关系
		cur = new Node(data);
		cur->_parent = parent;
		if (kot(parent->_data) < kot(data))//cur插入在parent的右孩子处
			parent->_right = cur;
		else
			parent->_left = cur;//cur插入在parent的左孩子处
		cur->_col = RED;//将插入的结点设置为红色

		//step2:检查新增结点后，是否还满足红黑树性质
		//……


	}
	
	Node* _root = nullptr;
};

  
  

3、map、set封装Ⅱ：迭代器实现

3.1、基本说明

  1）、基本说明
  通常情况下，begin()与end()代表的是一段前闭后开的区间。反映到红黑树中，begin()表示中序遍历下第一个结点（即最左侧结点/最小结点）；end()表示最后一个结点的下一个位置(即最右侧结点/最大结点)。

  一种实现方案：通常情况下会给出一个header头结点，类似于链表中的哨兵位头，其left、right分别指向最左结点和最右结点，即我们需要的begin()、end()。
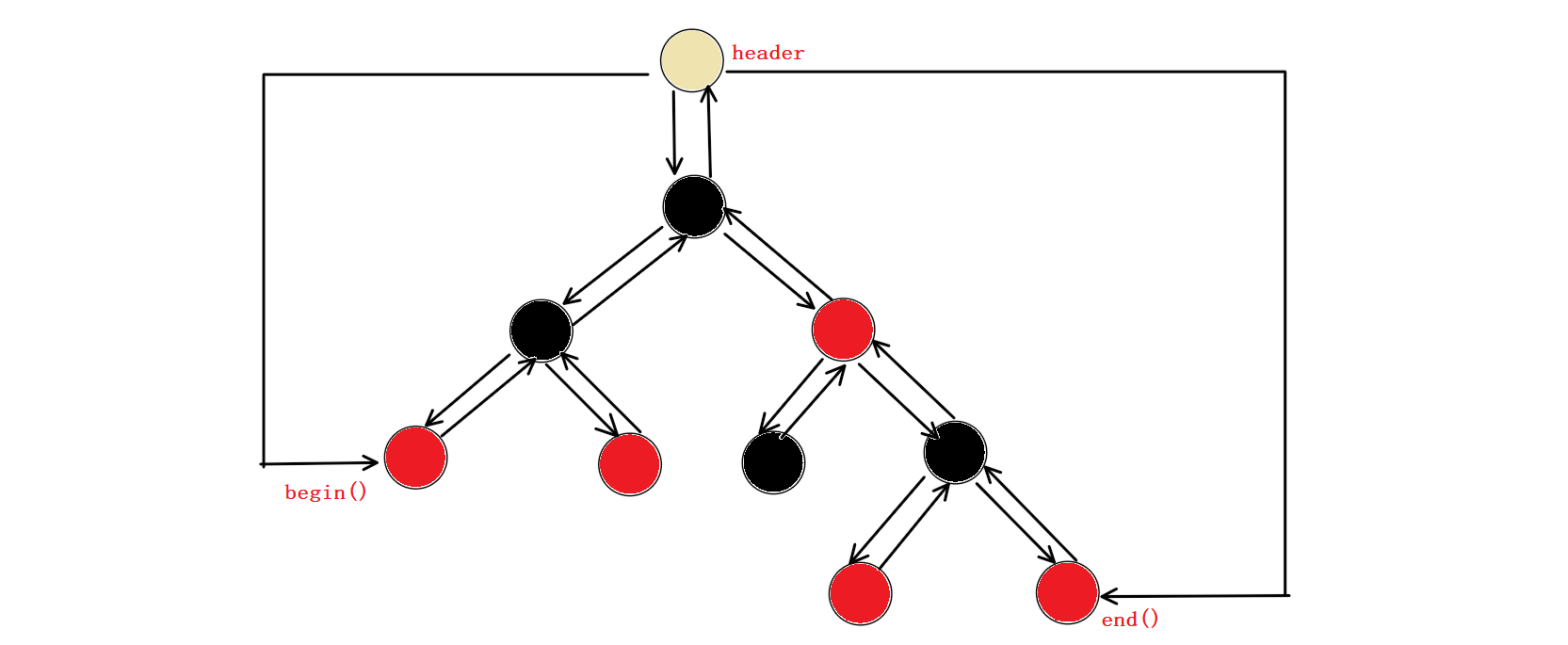
在这里插入图片描述

  后续实现中我们并没有借鉴哨兵位的头。
  说明：set、map的迭代器，实则使用的是红黑树的迭代器，因此实现时，我们需要先实现红黑树中的迭代器，对set、map而言，则通过封装达成相关需求。
  
  红黑树中，迭代器基本框架如下：类比于List迭代器实现。

template<class T, class Ref, class Ptr>
struct __RBTreeIterator
{
	typedef RBTreeNode<T> Node;
	typedef __RBTreeIterator<T, Ref, Ptr> iterator;

	Node* _node;//成员变量：指向结点的指针

	__RBTreeIterator(Node* node)//构造函数
		:_node(node)
	{}

	//实现++、--、*、&等
	//……

};

  
  

3.2、begin()、end()、operator*、operator&、operator==、operator!=

3.2.1、begin()、end()

  1）、在红黑树中

template<class K, class T, class KeyOfT>
struct RBTree
{
	typedef RBTreeNode<T> Node;
	typedef __RBTreeIterator<T, T&, T*> iterator;
	typedef __RBTreeIterator<T, const T&, const T*> const_iterator;

public:

	iterator begin()
	{	//begin()在红黑树中取最左结点
		Node* cur = _root;
		while (cur && cur->_left)
		{
			cur = cur->_left;
		}
		return iterator(cur);//匿名构造
	}

	iterator end()
	{
		return iterator(nullptr);
	}
	
	//……

}

  
  2）、在map、set中
  map、set中迭代器只需要调用红黑树的迭代器即可。注意此处typename的使用说明。

		typedef typename RBTree<K, K, SetKeyofT>::iterator iterator;
		iterator begin()
		{
			return _t.begin();
		}

		iterator end()
		{
			return _t.end();
		}

		typedef typename RBTree<K, pair<K, V>, MapKeyofT>::iterator iterator;
		iterator begin()
		{
			return _t.begin();
		}

		iterator end()
		{
			return _t.end();
		}

  
  
  

3.2.2、operator*、operator&、operator==、operator!=

	Ref operator* ()
	{
		return _node->_data;
	}

	Ptr operator&()
	{
		return &(_node->_data);
	}

	bool operator==(const iterator& it)const
	{
		return _node == it._node;
	}

	bool operator!=(const iterator& it)const
	{
		return _node != it._node;
	}

  
  

3.3、operator++、operator- -

3.3.1、operator++

  红黑树中，operator++要满足中序遍历，访问当前结点的下一个位置，此时会存在两种情况：
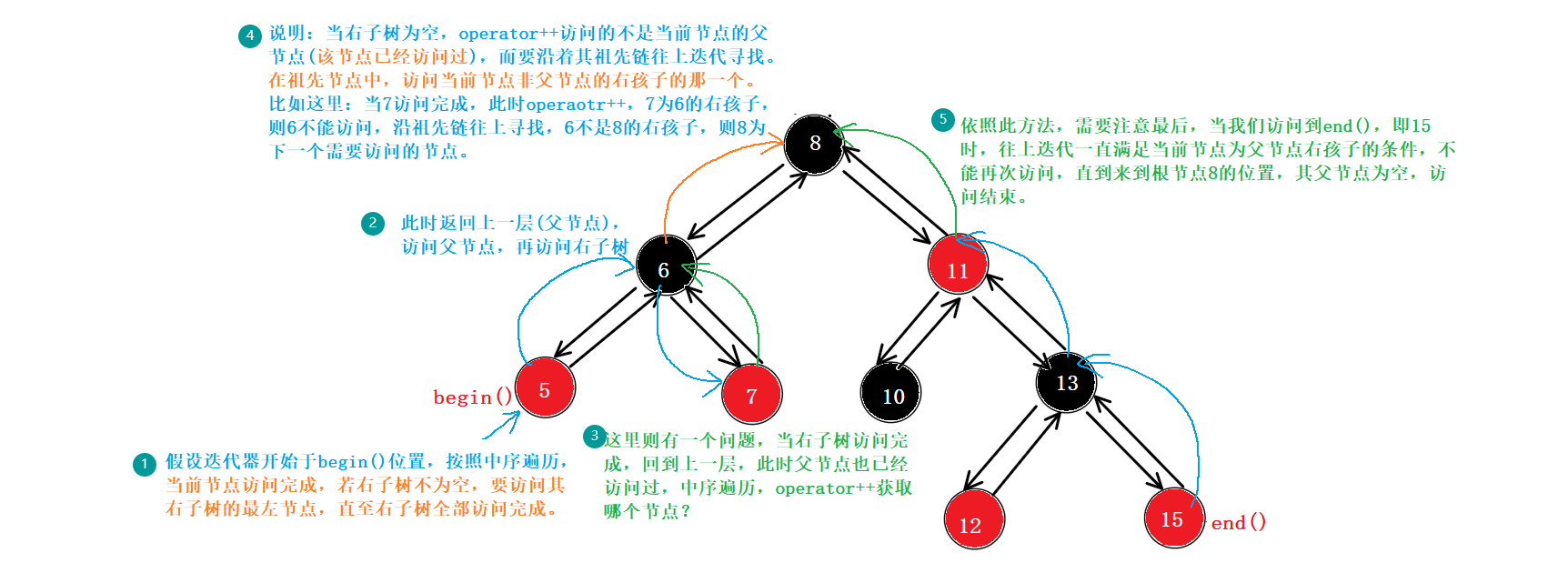
在这里插入图片描述

  2）、相关实现

	iterator& operator++()
	{
		if (_node->_right)//当前节点右子树不为空：访问其右子树最左节点
		{
			Node* cur = _node->_right;
			while (cur->_left)
				cur = cur->_left;
			_node = cur;//让迭代器来到当前结点处
		}
		else//当前节点右子树为空：沿祖先链迭代，寻找首个孩子非右孩子的父节点
		{
			Node* cur = _node;
			Node* parent = _node->_parent;
			while (parent && cur == parent->_right)
			{
				cur = parent;
				parent = cur->_parent;
			}
			_node = parent;//此处迭代器来到的是parent位置处
		}

		return *this;//最后返回迭代器本身
	}

  
  

3.3.2、operator- -

  反方向进行即可。

	iterator operator--()
	{
		if (_node->_left)
		{
			Node* cur = _node->_left;
			while (cur && cur->_left)
				cur = cur->_left;
			_node = cur;
		}
		else
		{
			Node* cur = _node;
			Node* parent = cur->_parent;
			while (parent && cur == parent->_left)
			{
				cur = parent;
				parent = cur->_parent;
			}
			_node = cur;
		}
	}

  
  
  

3.4、Insert满足pair<iterator,bool>返回值、operator[]

3.4.1、Insert

  在之前学习map、set时，对insert的返回值我们有简单介绍：
在这里插入图片描述
  这里我们同样做出修改：

	pair<iterator,bool> Insert(const T& data)
	{
		KeyOfT kot;

		//step1：按照二叉搜索树的方式插入新节点
		Ⅰ、寻找位置
		if (_root == nullptr)
		{
			_root = new Node(data);
			_root->_col = BLACK;
			return make_pair(iterator(_root), true);//返回新增节点处的迭代器及bool值
		}

		//根节点不为空：
		Node* cur = _root;
		Node* parent = nullptr;
		while (cur)
		{
			//比较当前结点值和待插入值
			if (kot(cur->_data) < kot(data))
			{
				parent = cur;
				cur = cur->_right;
			}
			else if (kot(cur->_data) > kot(data))
			{
				parent = cur;
				cur = cur->_left;
			}
			else
			{
				return make_pair(iterator(cur),false);//key值已存在：返回原先存在的节点的迭代器
			}
		}

		Ⅱ、插入值，调整链接关系
		cur = new Node(data);
		Node* newnode = cur;//用于返回
		cur->_parent = parent;
		if (kot(parent->_data) < kot(data))
			parent->_right = cur;
		else
			parent->_left = cur;
		cur->_col = RED;

		//step2:检查新增结点后，是否还满足红黑树性质
		//此处省略
		
		_root->_col = BLACK;
		return make_pair(iterator(newnode), true);//返回新增节点处的迭代器及bool值

	}

  
  
  

3.4.2、operator[]

  有了上述对于insert的改造，map中operator[]就能够实现(此处的相关解释见前文：set和map（一）)

		V& operator[](const K& key)
		{
			pair<iterator, bool> ret = insert(make_pair(key, V()));
			return ret.first->second;//rer.first获取iterator，iterator调用opeator->
		}

  
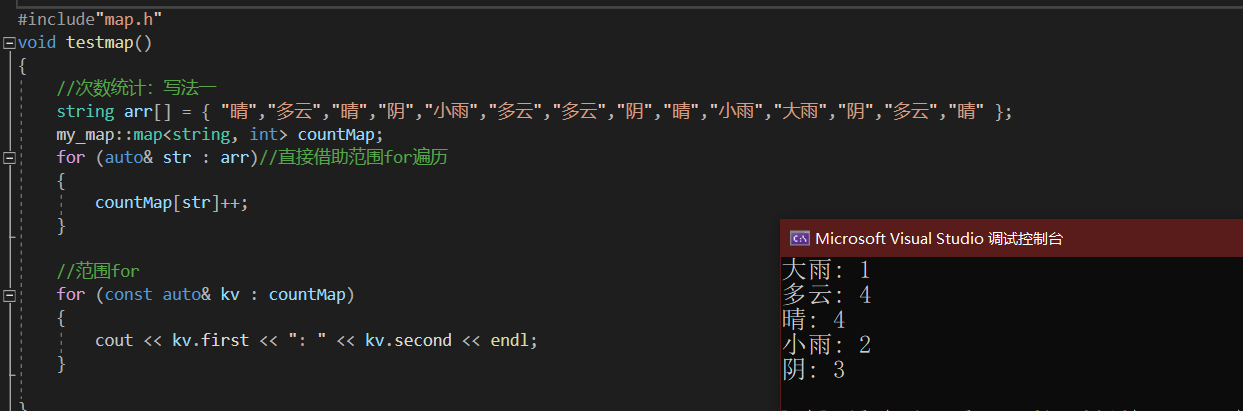
  测试代码如下：


#include"map.h"
void testmap()
{
	//次数统计
	string arr[] = { "晴","多云","晴","阴","小雨","多云","多云","阴","晴","小雨","大雨","阴","多云","晴" };
	my_map::map<string, int> countMap;
	for (auto& str : arr)//直接借助范围for遍历
	{
		countMap[str]++;
	}

	//范围for
	for (const auto& kv : countMap)
	{
		cout << kv.first << ": " << kv.second << endl;
	}

}

在这里插入图片描述

  
  
  

4、总览

4.1、set

#pragma once

#include"RedBlackTree.h"


namespace my_set
{
	template<class K>
	class set
	{
		struct SetKeyofT
		{
			const K& operator()(const K& key)
			{
				return key;
			}
		};

	public:

		typedef typename RBTree<K, K, SetKeyofT>::iterator iterator;
		iterator begin()
		{
			return _t.begin();
		}

		iterator end()
		{
			return _t.end();
		}

		pair<iterator,bool> insert(const K& val)
		{
			return _t.Insert(val);
		}

		

	private:
		RBTree<K, K, SetKeyofT> _t;
	};
}

  
  
  

4.2、map

#pragma once
#include"RedBlackTree.h"


namespace my_map
{
	template<class K, class V>
	class map
	{
	public:
		struct MapKeyofT
		{
			const K& operator()(const pair<K, V>& kv)
			{
				return kv.first;
			}
		};

		typedef typename RBTree<K, pair<K, V>, MapKeyofT>::iterator iterator;
		iterator begin()
		{
			return _t.begin();
		}

		iterator end()
		{
			return _t.end();
		}

		pair<iterator, bool> insert(const pair<K,V>& val)
		{
			return _t.Insert(val);
		}

		V& operator[](const K& key)
		{
			pair<iterator, bool> ret = insert(make_pair(key, V()));
			return ret.first->second;//rer.first获取iterator，iterator调用opeator->
		}
	private:
		RBTree<K, pair<K, V>, MapKeyofT> _t;
	};
}

  
  
  

4.3、RedBlackTree

#pragma once
#include<assert.h>
#include<iostream>
#include<utility>
using namespace std;



enum Colour
{
	RED,
	BLACK
};

template<class T>
struct RBTreeNode
{
	RBTreeNode<T>* _left;
	RBTreeNode<T>* _right;
	RBTreeNode<T>* _parent;

	T _data;//当前结点存储值
	Colour _col;

	RBTreeNode(const T& data)
		:_left(nullptr)
		,_right(nullptr)
		,_parent(nullptr)
		,_data(data)
		,_col(RED)
	{ }

};

template<class T, class Ref, class Ptr>
struct __RBTreeIterator
{
	typedef RBTreeNode<T> Node;
	typedef __RBTreeIterator<T, Ref, Ptr> iterator;

	Node* _node;//成员变量：指向结点的指针

	__RBTreeIterator(Node* node)//构造函数
		:_node(node)
	{}

	//实现++、--、*、->
	Ref operator* ()
	{
		return _node->_data;
	}

	Ptr operator->()
	{
		return &(_node->_data);
	}

	bool operator==(const iterator& it)const
	{
		return _node == it._node;
	}

	bool operator!=(const iterator& it)const
	{
		return _node != it._node;
	}

	iterator& operator++()
	{
		if (_node->_right)//当前节点右子树不为空：访问其右子树最左节点
		{
			Node* cur = _node->_right;
			while (cur->_left)
				cur = cur->_left;
			_node = cur;//让迭代器来到当前结点处
		}
		else//当前节点右子树为空：沿祖先链迭代，寻找首个孩子非右孩子的父节点
		{
			Node* cur = _node;
			Node* parent = _node->_parent;
			while (parent && cur == parent->_right)
			{
				cur = parent;
				parent = cur->_parent;
			}
			_node = parent;//此处迭代器来到的是parent位置处
		}

		return *this;//最后返回迭代器本身
	}


	iterator operator--()
	{
		if (_node->_left)
		{
			Node* cur = _node->_left;
			while (cur && cur->_left)
				cur = cur->_left;
			_node = cur;
		}
		else
		{
			Node* cur = _node;
			Node* parent = cur->_parent;
			while (parent && cur == parent->_left)
			{
				cur = parent;
				parent = cur->_parent;
			}
			_node = cur;
		}
	}
};

template<class K, class T, class KeyOfT>
struct RBTree
{
	typedef RBTreeNode<T> Node;
	typedef __RBTreeIterator<T, T&, T*> iterator;
	typedef __RBTreeIterator<T, const T&, const T*> const_iterator;

public:

	iterator begin()
	{	//begin()在红黑树中取最左结点
		Node* cur = _root;
		while (cur && cur->_left)
		{
			cur = cur->_left;
		}
		return iterator(cur);//匿名构造
	}

	iterator end()
	{
		return iterator(nullptr);
	}

	pair<iterator,bool> Insert(const T& data)
	{
		KeyOfT kot;

		//step1：按照二叉搜索树的方式插入新节点
		Ⅰ、寻找位置
		if (_root == nullptr)//单独处理：根节点为空时
		{
			_root = new Node(data);
			_root->_col = BLACK;//根节点默认为黑色
			return make_pair(iterator(_root), true);
		}

		//根节点不为空：
		Node* cur = _root;
		Node* parent = nullptr;
		while (cur)
		{
			//比较当前结点值和待插入值
			if (kot(cur->_data) < kot(data))//若当前结点值比待插入结点值小，说明待插入结点值在其右子树
			{
				parent = cur;
				cur = cur->_right;
			}
			else if (kot(cur->_data) > kot(data))
			{
				parent = cur;
				cur = cur->_left;
			}
			else//key值已存在
			{
				return make_pair(iterator(cur),false);
			}
		}

		Ⅱ、插入值，调整链接关系
		cur = new Node(data);
		Node* newnode = cur;//用于返回
		cur->_parent = parent;
		if (kot(parent->_data) < kot(data))//cur插入在parent的右孩子处
			parent->_right = cur;
		else
			parent->_left = cur;//cur插入在parent的左孩子处
		cur->_col = RED;//将插入的结点设置为红色

		//step2:检查新增结点后，是否还满足红黑树性质
		while (parent && parent->_col == RED)//新结点后，无论是cur本身，还是迭代后变色，如果parent、cur颜色皆红，则违反性质3：不能有连续的红结点，因此需要调整
		{
			//固定:
			Node* grandparent = parent->_parent;
			assert(grandparent && grandparent->_col == BLACK);//grandparent存在且为黑

			//关键看叔叔，此处对uncle和parent在不同位置分别处理
			if (parent == grandparent->_left)
			{
				Node* uncle = grandparent->_right;
				
				//情况一
				if (uncle&& uncle->_col == RED)//叔叔存在且为红
				{
					//处理方法：变色
					parent->_col = uncle->_col = BLACK;
					grandparent->_col = RED;
					//继续向上调整
					cur = grandparent;
					parent = cur->_parent;
				}
				else //叔叔不存在或叔叔存在且为黑：情况二+情况三
				{
					//处理方法：旋转+变色（旋转有四类）

					//Ⅰ：情况二：p在g左，c在p左，成直线。右单旋+g变色为红，p变色为黑
					if (cur == parent->_left)
					{
						RotateR(grandparent);
						grandparent->_col = RED;
						parent->_col = BLACK;
					}
					else//Ⅱ：情况三：p在g左，c在p右，成折线。左右双旋+g变色为红，c变色为黑
					{
						RotateL(parent);
						RotateR(grandparent);
						grandparent->_col = RED;
						cur->_col = BLACK;
					}
					break;//情况二、情况三完成调整后，满足红黑树规则，不必继续向上调整
				}
			}
			else//parent == grandparent->_right
			{
				Node* uncle = grandparent->_left;

				//情况一
				if (uncle&& uncle->_col == RED)//叔叔存在且为红
				{
					//处理方法：变色
					parent->_col = uncle->_col = BLACK;
					grandparent->_col = RED;
					//继续向上调整
					cur = grandparent;
					parent = cur->_parent;
				}
				else //叔叔不存在或叔叔存在且为黑：情况二+情况三
				{
					//处理方法：旋转+变色（旋转有四类）

					//Ⅰ：情况二：p在g右，c在p右，成直线。左单旋+g变色为红，p变色为黑
					if (cur == parent->_right)
					{
						RotateL(grandparent);
						grandparent->_col = RED;
						parent->_col = BLACK;
					}
					else//Ⅱ：情况三：p在g右，c在p左，成折线。右左双旋+g变色为红，c变色为黑
					{
						RotateR(parent);
						RotateL(grandparent);
						grandparent->_col = RED;
						cur->_col = BLACK;
					}
					break;//情况二、情况三完成调整后，满足红黑树规则，不必继续向上调整
				}
			}

		}
		_root->_col = BLACK;
		return make_pair(iterator(newnode), true);

	}


	void InOrder()
	{
		_InOrder(_root);
		cout << endl;
	}

	bool IsBalance()
	{
		if (_root == nullptr)
			return true;
		if (_root->_col == RED)
		{
			cout << "根节点不满足黑色" << endl;
			return false;
		}

		int BasicalNum = 0;//用于确定基准值：前序遍历时的第一条路径
		int blackNum = 0;//用于统计树中黑色结点数
		return PrevCheck(_root, blackNum, BasicalNum);
	}

private:
	bool PrevCheck(Node* root, int blackNum, int& basicalNum)
	{
		if (root == nullptr)
		{
			if (basicalNum == 0)
			{
				basicalNum == blackNum;
				return true;
			}
			else
			{
				if (blackNum == basicalNum)
					return true;
				else
				{
					cout << "某条路径黑色结点数不匹配" << endl;
					return false;
				}
			}
		}

		if (root->_col == BLACK)
			++blackNum;
		if (root->_col == RED && root->_parent->_col == RED)
		{
			cout << "存在连续的红色结点" << endl;
			return false;
		}

		return PrevCheck(root->_left, blackNum, basicalNum)
			&& PrevCheck(root->_right, blackNum, basicalNum);
	}

	void _InOrder(Node* root)
	{
		if (root == nullptr)
			return;
		_InOrder(root->_left);
		//cout << root->_kv.first << "," << root->_kv.second << endl;
		_InOrder(root->_right);
	}

	void RotateL(Node* parent)
	{
		Node* subR = parent->_right;
		Node* subRtoL = subR->_left;
		Node* grendparent = parent->_parent;

		//修改链接关系以达成旋转
		parent->_right = subRtoL;
		parent->_parent = subR;

		if (subRtoL)//h>=0，subRtoL可能不存在
			subRtoL->_parent = parent;

		subR->_left = parent;
		if (_root == parent)//parent为原先AVL树的根节点
		{
			subR->_parent = nullptr;
			_root = subR;
		}
		else//parent为原先AVL树的分支节点
		{
			subR->_parent = grendparent;
			if (grendparent->_left == parent)
				grendparent->_left = subR;
			else
				grendparent->_right = subR;
		}
	}


	void RotateR(Node* parent)
	{
		Node* subL = parent->_left;
		Node* subLtoR = subL->_right;
		Node* grendparent = parent->_parent;

		//处理链接关系
		parent->_left = subLtoR;
		parent->_parent = subL;

		if (subLtoR)
			subLtoR->_parent = parent;

		subL->_right = parent;
		if (_root == parent)
		{
			subL->_parent = nullptr;
			_root = subL;
		}
		else
		{
			subL->_parent = grendparent;
			if (grendparent->_left == parent)
				grendparent->_left = subL;
			else
				grendparent->_right = subL;
		}
	}

	Node* _root = nullptr;
};

  
  
  
  
  
  
  
  
  

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/528854.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

( 位运算 ) 693. 交替位二进制数 / 476. 数字的补数 ——【Leetcode每日一题】

( 位运算 ) 693. 交替位二进制数 / 476. 数字的补数 ——【Leetcode每日一题】

❓ 题目一 693. 交替位二进制数 难度&#xff1a;简单 给定一个正整数&#xff0c;检查它的二进制表示是否总是 0、1 交替出现&#xff1a;换句话说&#xff0c;就是二进制表示中相邻两位的数字永不相同。 示例 1&#xff1a; 输入&#xff1a;n 5 输出&#xff1a;true 解…
阅读更多...
使用inbuilder完成UBML低代码设计

使用inbuilder完成UBML低代码设计

文章目录 一、活动介绍二、我所认识的低代码平台三、使用inbuilder开发工具拖拉跩实现 低代码产品开发四、环境搭建五、5分钟完成低代码实验六、财务报销报表实验活动成果截图七、总结 一、活动介绍 开放原子训练营开启inBuilder低代码实验室活动。无论您是计算机行业相关从业…
阅读更多...
(css)el-select多选以tag展示时，超过显示长度以...省略号显示

(css)el-select多选以tag展示时，超过显示长度以...省略号显示

(css)el-select多选以tag展示时&#xff0c;超过显示长度以…省略号显示 效果 代码&#xff1a; <span>系统词典维度&#xff1a;</span><el-selectv-model"dNum"placeholder"请选择"multiplecollapse-tags //设置collapse-tags属性将它…
阅读更多...
Windows批处理指令

Windows批处理指令

前言 批处理文件&#xff08;batch file&#xff09;包含一系列 DOS 命令&#xff0c;通常用于自动执行重复性任务。用户只需双击批处理文件便可执行任务&#xff0c;而无需重复输入相同指令。编写批处理文件非常简单&#xff0c;但难点在于确保一切按顺序执行。编写严谨的批处…
阅读更多...
Java进阶-面向对象入门

Java进阶-面向对象入门

1. 面向过程与面向对象 1.1 何谓“面向对象”的编程思想&#xff1f; 首先解释一下“思想”。 先问你个问题&#xff1a;你想做个怎样的人&#xff1f; 可能你会回答&#xff1a;我想做个好人&#xff0c;孝敬父母&#xff0c;尊重长辈&#xff0c;关爱亲朋…… 你看&#…
阅读更多...
2023年Android开发者路线-第2部分

2023年Android开发者路线-第2部分

2023年Android开发者路线-第1部分 2023年Android开发者路线-第2部分 2023年Android开发者路线-第3部分 2023年Android开发者路线-第4部分 2023Android开发者路线-第2部分 在上一篇文章中&#xff0c;我们讨论了 Android 架构的重要元素&#xff0c;包括主要的 Android 语言…
阅读更多...
探索iOS之AVFoundation框架

探索iOS之AVFoundation框架

AVFoundation框架的业务层主要是AVKit和UIKit&#xff0c;内核层包括CoreVideo、CoreAudio、CoreMedia、VideoToolBox等。AVFoundation作为iOS的音视频框架&#xff0c;提供音视频播放、录制、编辑、编解码、音效设置等。接下来&#xff0c;让我们看一下整体的框架图。 一、AVK…
阅读更多...
ANR基础篇 - Trace.txt文件分析

ANR基础篇 - Trace.txt文件分析

系列文章目录 提示&#xff1a;这里可以添加系列文章的所有文章的目录&#xff0c;目录需要自己手动添加 例如&#xff1a;第一章 Python 机器学习入门之pandas的使用 文章目录 系列文章目录前言一、trace.txt文件示例二、日志分析2.1 CPU 负载2.2 内存信息2.3 堆栈信息schedst…
阅读更多...
Mybatis 案例

Mybatis 案例

文章目录 Mybatis 案例一、 准备工作1.1 数据库表1.2 Restfull规范1.3 封装结果类1.4 实体类 二、部门管理2.1 查询全部部门信息2.2 删除部门2.3 新增部门 三、员工管理3.1 分页查询3.2 分页查询 - PageHelper插件3.3 分页查询 - 条件查询3.4 批量删除员工3.5 新增员工3.6 修改…
阅读更多...
蓝桥杯模块学习3——蜂鸣器与继电器

蓝桥杯模块学习3——蜂鸣器与继电器

第一章 硬件部分 1.1 电路的组成部分 1.1.1 译码器和锁存器 具体可回顾之前LED灯的文章&#xff1a; https://blog.csdn.net/weixin_63568691/article/details/130660096 1.1.2 ULN2003达林顿管 原理图&#xff1a; 功能&#xff1a; &#xff08;1&#xff09;改变电路特性…
阅读更多...
使用Spring初始化器创建Spring Boot项目

使用Spring初始化器创建Spring Boot项目

注&#xff1a;初始化向导需要联网创建Spring Boot项目 new project 项目创建完成 resources 文件夹中目录结构&#xff1a; static &#xff1a;保存所有的静态资文件&#xff0c; js css images templates &#xff1a;保存所有的模板页面&#xff08;Spring Boot默认j…
阅读更多...
python3 爬虫相关学习1：安装requests模块

python3 爬虫相关学习1：安装requests模块

目录 1 安装前&#xff1a;避免python2 python3 引起的问题 2 如何安装python3 2.1 直接上python3 官网下载 2.2 或者windows的话&#xff0c;microsoft store 里也可以下载 2.3 查看python版本 3 安装requests模块 3.1 很可能安装requests模块之前会遇到报错&#xff…
阅读更多...
linux0.12-8-11-vsprintf.c

linux0.12-8-11-vsprintf.c

[383页] 1、 这一小节可以不看代码如何实现&#xff0c;因为标准的C库函数&#xff1b; 2、 等自己看完的这本书&#xff0c;有兴趣过来研究研究也是可以的。 8-11 vsprintf.c程序 8-11-1 功能描述 该程序主要包括vsprintf(),用于对参数产生格式化的输出。由于该函数是C函数…
阅读更多...
SOME/IP 草稿

SOME/IP 草稿

SOME/IP 名词解释 SOME/IP 全称是 Scalable service-Oriented MiddlewarE over IP。也就是基于 IP 协议的面向服务的可扩展性通信中间件协议。 面向服务 SOA基于 IP 协议之上的通信协议中间件 SOME/IP 功能 服务发现 (Service Discovery)远程服务调用 &#xff08;RPC,rem…
阅读更多...
React面试题汇总 --2

React面试题汇总 --2

1. 何为 redux &#xff0c;解决什么问题 操作流程 使用场景 优缺点 &#xff1f; Redux使用详解(一) Redux的核心思想与基本使用__聪明勇敢有力气的博客-CSDN博客Redux使用详解(一) Redux的核心思想与基本使用https://blog.csdn.net/weixin_65402230/article/details/128193…
阅读更多...
全免费开源-国内搭建ChatGPT个人镜像站与维护全攻略

全免费开源-国内搭建ChatGPT个人镜像站与维护全攻略

全免费开源-国内搭建ChatGPT个人镜像站与维护全攻略 准备阶段部署网站腾讯云注册与解析添加API和密码更换域名的配置多密码管理密码更换密码批量生成 本教程收集于&#xff1a;AIGC从入门到精通教程汇总 全免费开源&#xff0c;仅需一个域名就可以部署国内的ChatGPT镜像版本。…
阅读更多...
ConvTranspose2d 的简单例子理解

ConvTranspose2d 的简单例子理解

文章目录 参考基础概念简单例子&#xff1a; stride2step1step2step3 参考 逆卷积的详细解释ConvTranspose2d&#xff08;fractionally-strided convolutions)nn.ConvTranspose2d的参数output_padding的作用 基础概念 逆卷积&#xff0c;也叫反卷积或者转置卷积&#xff0c;…
阅读更多...
故障分析 | OceanBase 频繁更新数据后读性能下降的排查

故障分析 | OceanBase 频繁更新数据后读性能下降的排查

本文摘要 本文分析并复现了 OceanBase 频繁更新数据后读性能下降现象的原因&#xff0c;并给出了性能改善建议。 背景 测试在做 OceanBase 纯读性能压测的时候&#xff0c;发现对数据做过更新操作后&#xff0c;读性能会有较为明显的下降。具体复现步骤如下。 复现方式 环…
阅读更多...
部门新来一00后，给我卷崩溃了...

部门新来一00后，给我卷崩溃了...

2022年已经结束结束了&#xff0c;最近内卷严重&#xff0c;各种跳槽裁员&#xff0c;相信很多小伙伴也在准备今年的金三银四的面试计划。 在此展示一套学习笔记 / 面试手册&#xff0c;年后跳槽的朋友可以好好刷一刷&#xff0c;还是挺有必要的&#xff0c;它几乎涵盖了所有的…
阅读更多...
NFT数字藏品平台

NFT数字藏品平台

在 NFT &#xff08;非同质化代币&#xff09;发行和交易中&#xff0c;数字藏品交易平台&#xff08;以下简称“交易平台”&#xff09;的运营模式和法律地位至关重要。本文对数字藏品交易平台的运营方式进行梳理&#xff0c;并对其中可能存在的法律风险进行分析。 2021年以来…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023