参考

• 逆卷积的详细解释ConvTranspose2d（fractionally-strided convolutions)
• nn.ConvTranspose2d的参数output_padding的作用

基础概念

逆卷积，也叫反卷积或者转置卷积，作用是对图像进行上采样。
参考链接中的文章对形状变化的公式做了较为详细的描述，这里简单使用一个例子来演示数据变换过程。

假如输入数据(也叫原始数据）形状为 H x W, H = W.
大概的流程可以描述为

• 当stride >1, 对原始数据进行插值变换，也就是每相邻数据间插入 (s-1) 列/行数据，变换后数据形状为
  $$H_{new}=W_{new}=H+(s-1)\ast (H-1)$$
• 对变换后的数据进行padding，
  $$paddin{g}_{new}=kernel\_size-padding-1$$
  经过这一步之后，数据形状为
  $$H_{new}+2\ast paddin{g}_{new}$$
• 在这两步变换后进行如下正常卷积运算
  kernel_size = kernel_size
  padding = 0
  stride = 1

简单例子： stride=2

h = w = 2
stride = 2
p = 0
kernel_size = 3

step1

原始数据：

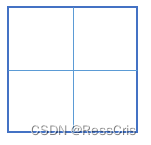
step2

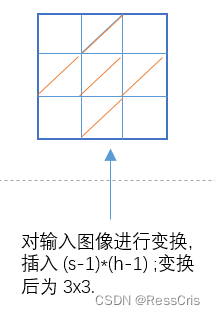
内部变换：
stride >1,
当卷积时设置的stride>1时，将对输入的特征图y进行插值操作(interpolation)。

即需要在输入的特征图y的每个相邻值之间插入(stride-1)行和列0，因为特征图中能够插入的相邻位置有(height-1)个位置，所以此时得到的特征图的大小由HoutHout(Hout即height) 变为新的 Hout_newHout_new，即[Hout + (stride-1) * (Hout-1)] * [Hout + (stride-1) * (Hout-1)]

step3

外部变换：
为了实现由HoutHout大小的y逆卷积得到HinHin大小的x，还需要设置padding_new的值为(kernel_size - padding - 1),这里的padding是卷积操作时设置的padding值

然后在这个变换好的图上进行 kernel_size=3, padding =0, stride =1 的正常卷积可以得到最终结果
按照卷积的变换公式计算得到

(w + 2p - kernel_size)/s +1 = (7 - 3) +1 = 5.

也就是得到 5x5 的数据。