目录
- 主析取范式 主合取范式
- 推理理论(假设前提条件为真推出的结论)
- 真值表法
- 直接证明法
- ** 常用推理公式 **
- 间接证明 CP规则--附加前提证明法,证明比较方便 单条件形式,提取前件
- 间接法 归谬法 结论是单命题,取反前提引入
- 常用 latex 定义
主析取范式 主合取范式
推理理论(假设前提条件为真推出的结论)
| 极小项 | 极大项 | ||||
| 合并第一行 | |||||
| 合并第二行 | |||||
真值表法
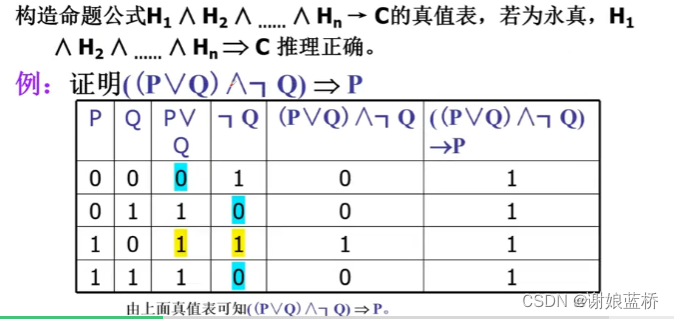
直接证明法
常用推理规则—倒着看,推理整理过程
P规则(前提引入)
T规则(结论引入)
** 常用推理公式 **
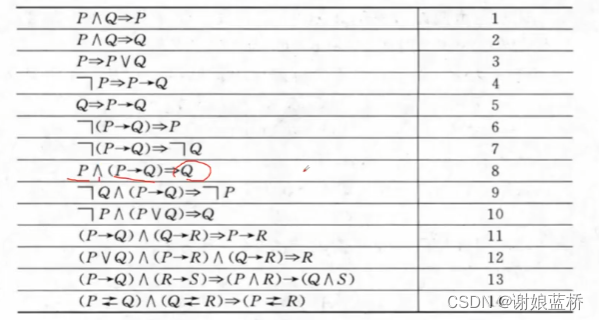
| 名称 | 内容 |
|---|---|
| 附加率 | A ⇒ ( A ∨ B ) ¬ A ⇒ A → B B ⇒ A → B A\Rightarrow(A\lor B)\qquad\\\neg A\Rightarrow A\to B\\B\Rightarrow A\to B A⇒(A∨B)¬A⇒A→BB⇒A→B |
| 化简率 | A ∧ B ⇒ B A ∧ B ⇒ A ¬ ( A → B ) ⇒ A ¬ ( A → B ) ⇒ ¬ B A\wedge B\Rightarrow B\\A\land B \Rightarrow A\\\neg(A\to B)\Rightarrow A\\ \neg(A\to B)\Rightarrow\neg B A∧B⇒BA∧B⇒A¬(A→B)⇒A¬(A→B)⇒¬B |
| 析取三段论 | ( A ∨ B ) ∧ ¬ A ⇒ B (A\lor B)\wedge\neg A\Rightarrow B (A∨B)∧¬A⇒B |
| 假言推理/分离定律 | ( A → B ) ∧ A ⇒ B (A\to B)\wedge A\Rightarrow B (A→B)∧A⇒B |
| 拒取式 | ( A → B ) ∧ ¬ B ⇒ ¬ A (A\to B)\wedge\neg B\Rightarrow\neg A (A→B)∧¬B⇒¬A |
| 假言三段论 | ( A → B ) ∧ ( B → C ) ⇒ A → C (A\to B)\wedge(B\to C)\Rightarrow A\to C (A→B)∧(B→C)⇒A→C |
| 等价三段论 | ( A ↔ B ) ∧ ( B ↔ C ) ⇒ A ↔ C (A\leftrightarrow B)\land(B\leftrightarrow C)\Rightarrow A\leftrightarrow C (A↔B)∧(B↔C)⇒A↔C |
| 构造性二难 | ( A → B ) ∧ ( C → D ) ∧ ( A ∨ C ) ⇒ B ∨ D (A\to B)\land(C\to D)\land(A\lor C)\Rightarrow B\lor D (A→B)∧(C→D)∧(A∨C)⇒B∨D |
| 破环性二难 | ( A → B ) ∧ ( C → D ) ∧ ( ¬ B ∨ ¬ D ) ⇒ ¬ A ∨ ¬ C (A\to B)\land(C\to D)\land(\lnot B\lor \lnot D)\Rightarrow \lnot A\lor \lnot C (A→B)∧(C→D)∧(¬B∨¬D)⇒¬A∨¬C |

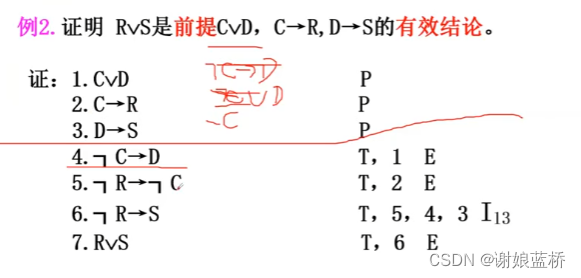
间接证明 CP规则–附加前提证明法,证明比较方便 单条件形式,提取前件
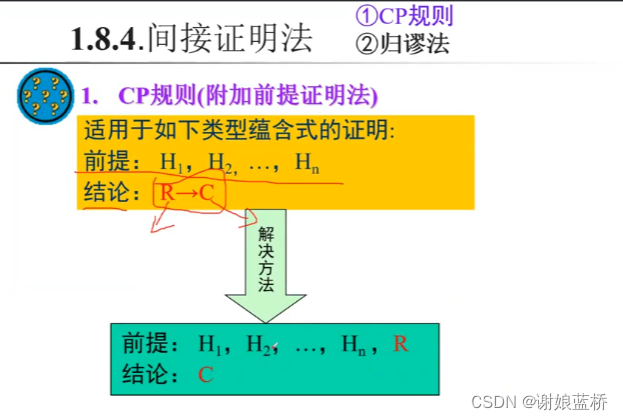



间接法 归谬法 结论是单命题,取反前提引入
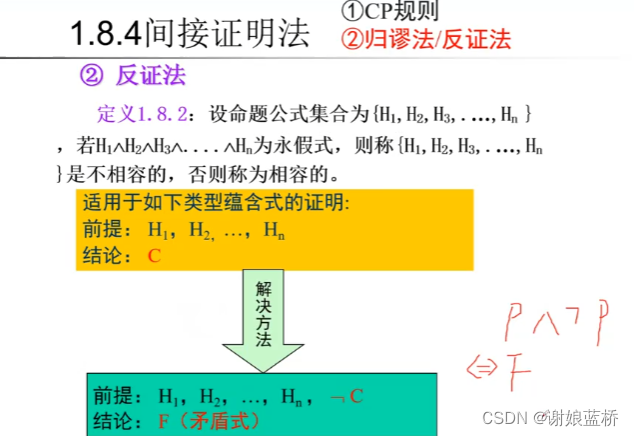

常用 latex 定义
上标: x ( n ) 下标 x ( 1 ) 分数 : 1 1 + 1 2 根号 : 1 + 1 + a 2 p 积分 : ∫ 1 ∞ 求和 : ∑ k = 1 n 1 k 不定积分 : ∫ a b f ( x ) d x 偏分 : ∂ E w ∂ w 极限 : lim 1 → ∞ 小于 < 大于 > 小于等于 ≤ 大于等于 ≥ 不等于 ≠ ≠ 不小于 ≮ 乘以 × 除法 ÷ 正负 ± 负正 ∓ 点乘法 x ⋅ y 空格 ∪ ∩ ∖ 包含 ⊂ ⊆ ⊊ ⊃ 属于 ∈ ∉ ∅ 空集合 ∅ 蕴含 → → ← 推理 ⇒ ⇐ ↦ 等价 ⇔ 合取 ∧ ∧ 析取 ∨ 非 ¬ ¬ 任意 ∀ 存在 ∃ 左括号右括号 { } ⊤ ⊥ ⊢ ⊨ ⋆ ∗ ⊕ ∘ ∙ ≈ ∼ ≅ ≡ ≺ ∞ ℵ ∇ ∂ ϵ ε ϕ φ { ∑ i = 0 n i 2 = ( n 2 + n ) ( 2 n + 1 ) 6 } ( ∑ k = 1 2 N 2 1 k ) ∂ f ( x , y ) ∂ x ∣ x = 0 { a a a } { 联合公式 a 1 x + b 1 y + c 1 z = d 1 + e 1 a 2 x + b 2 y = d 2 a 3 x + b 3 y + c 3 z = d 3 } 条件格式 f ( n ) { n / 2 i f n > 10 n + 1 i f n = 10 上标:x^{(n)}\\ 下标 x_{(1)}\\ 分数:\frac{1}{1+\frac{1}{2}}\\ 根号:\sqrt{1+\sqrt[^p]{1+a^2}}\\ 积分:\int_1^\infty\\ 求和:\sum_{k=1}^n\frac{1}{k}\\ 不定积分:\int_a^b f(x)dx\\ 偏分:\frac{\partial E_w}{\partial w}\\ 极限:\lim_{1\to\infty}\\ 小于\lt \\ 大于\gt \\ 小于等于\le \\ 大于等于\ge \\ 不等于 \neq \neq \\ 不小于\not\lt \\ 乘以\times\\ 除法 \div\\ 正负 \pm 负正\mp \\ 点乘法x \cdot y\\ 空格 \qquad\\ \cup \cap \setminus\\ 包含 \subset \subseteq \subsetneq \supset \\ 属于\in \notin \emptyset \\ 空集合\varnothing\\ 蕴含\to \rightarrow \leftarrow \\ 推理\Rightarrow \Leftarrow \mapsto\\ 等价 \Leftrightarrow\\ 合取\land \wedge \\ 析取\lor \\ 非\lnot \neg \\ 任意\forall\\ 存在 \exists \\ 左括号 右括号 \left \lbrace \right\rbrace\\ \top \bot \vdash \vDash\qquad \star \ast \oplus \circ \bullet\qquad \approx \sim \cong \equiv \prec\qquad \infty \aleph \nabla \partial\qquad \epsilon \varepsilon\qquad \phi \varphi\\ \left \lbrace \sum_{i=0}^n i^2 = \frac{(n^2+n)(2n+1)}{6} \right\rbrace \\ \left( \sum_{k=\frac{1}{2}}^{N^2}\frac{1}{k} \right)\\ \left. \frac{\partial f(x, y)}{\partial x}\right|_{x=0}\\ \left\lbrace\begin{aligned}a\\a\\a\\\end{aligned}\right\rbrace \\ \left\lbrace\begin{aligned} 联合公式\\ a_1x+b_1y+c_1z &=d_1+e_1 \\\ a_2x+b_2y &=d_2 \\\ a_3x+b_3y+c_3z &=d_3 \end{aligned}\right\rbrace \\ \\ 条件格式\\ f(n) \begin{cases} n/2&if\;n>10\\ n+1&if\;n=10\\ \end{cases}\qquad 上标:x(n)下标x(1)分数:1+211根号:1+p1+a2积分:∫1∞求和:k=1∑nk1不定积分:∫abf(x)dx偏分:∂w∂Ew极限:1→∞lim小于<大于>小于等于≤大于等于≥不等于==不小于<乘以×除法÷正负±负正∓点乘法x⋅y空格∪∩∖包含⊂⊆⊊⊃属于∈∈/∅空集合∅蕴含→→←推理⇒⇐↦等价⇔合取∧∧析取∨非¬¬任意∀存在∃左括号右括号{}⊤⊥⊢⊨⋆∗⊕∘∙≈∼≅≡≺∞ℵ∇∂ϵεϕφ{i=0∑ni2=6(n2+n)(2n+1)} k=21∑N2k1 ∂x∂f(x,y) x=0⎩ ⎨ ⎧aaa⎭ ⎬ ⎫⎩ ⎨ ⎧联合公式a1x+b1y+c1z a2x+b2y a3x+b3y+c3z=d1+e1=d2=d3⎭ ⎬ ⎫条件格式f(n){n/2n+1ifn>10ifn=10