前情提要：https://blog.csdn.net/weixin_45434953/article/details/130604086

正规方程

正规方程能以更好的方式求得假设函数中$\theta$的最优值。它提供了一种用于求$\theta$的解析方法，而不是梯度下降那样的迭代方法。也就是只需要一次运算就可以得出结果。设有一个代价函数$$J({\theta }_0,{\theta }_1...,{\theta }_n)=\frac{1}{2m}\sum _{i=1}^m(h_{\theta }(x^{(i)})-y^{(i)}{)}^2$$那么我们对于每一个$j\in (0,m)$令$$\frac{\partial }{\partial {\theta }_j}J(\theta )=0$$，然后求出${\theta }_j$的值。根据微积分，我们知道函数$f(x)$若在$x=x_0$取得最小值$f(x_0)=f_{min}(x)$，那么在$x_0$处$f(x)$的导数$f^{\prime }(x_0)$一定为0。反过来，导数为0的位置不一定是最值。

假设现在的数据样本如下：

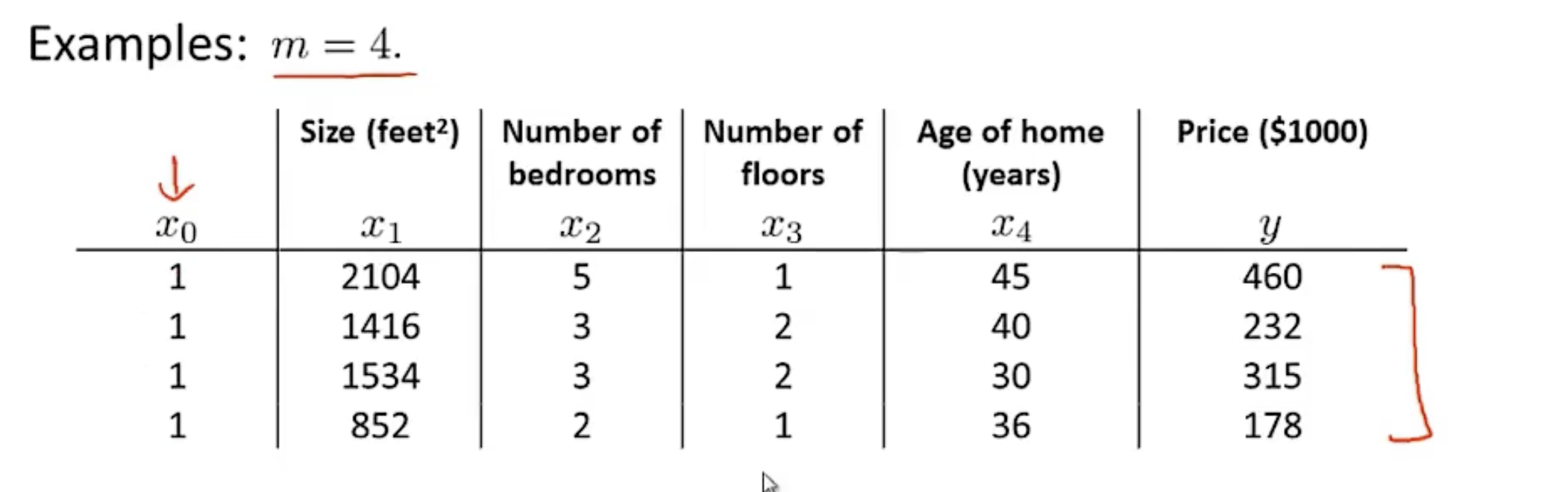
前面说过，$x_0$是恒等于1的。那么实际上我们可以根据上述的数据构建如下的矩阵：
$$X=\left[\begin{array}{ccccc}1& 2104& 5& 1& 45\\ 1& 1416& 3& 2& 40\\ 1& 1534& 3& 2& 30\\ 1& 852& 2& 1& 36\end{array}\right],y=\left[\begin{array}{c}460\\ 232\\ 315\\ 178\end{array}\right]$$
那么，计算$\theta$的方法是:
$$\theta =(X^{T}X{)}^{-1}{X}^{T}y$$

需要注意的是，正规方程不需要使用特征缩放。

正规方程和梯度下降的对比：
梯度下降需要选择学习速率，并且需要迭代，而正规方程不需要。但是对于特征量n较大的情况，$(X^{T}X{)}^{-1}$会消耗大量的时间，通常认为正规方程的时间复杂度为O(n³)，因此梯度下降更适合应对n较大的情况，一般以n=10000为分界线。而且梯度下降在很多算法中都会广泛的应用，但是正规方程一般只用于线性回归。