考古：Transformer

news2025/1/21 4:49:09

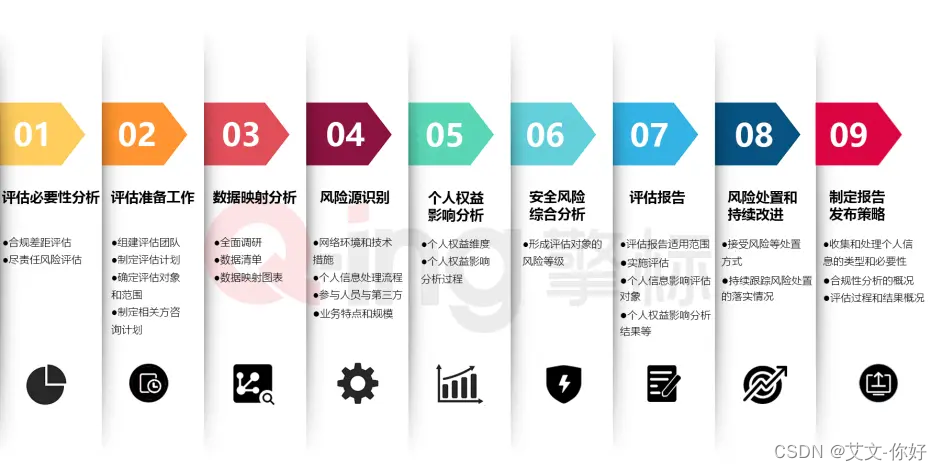
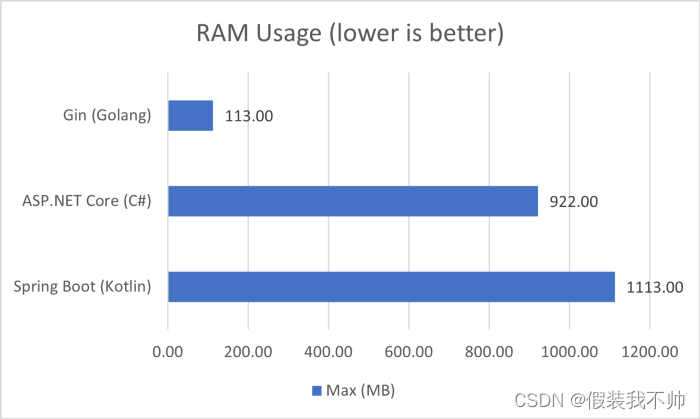
论文1: 《Attention is all you need》

模型体系结构

Encoder 将符号表示的输入序列 $x_1,...,x_n)$ 映射到连续表示的序列 $z=(z_1,...,z_n)$ 。给定 $z$ ，Encoder 然后一次产生一个元素的符号输出序列 $y_1，…，y_m)$ 。
在每一步，模型都是自回归的，在生成下一步时，将先前生成的符号作为附加输入。

Transformer 架构：

Encoder： Encoder有 $N = 6$ 层,每层有两个子层，第一层是多头注意力机制，第二层是简单的、位置全连接的前馈网络。在两个子层中的每一个子层周围使用残差连接，然后进行层归一化。即每个子层的输出为： $\tag{1} \textmd{LayerNorm}(x+\textmd{Sublayer(x))}$ 其中 $\textmd{Sublayer(x)}$ 是子层本身实现的函数。
在这里插入图片描述

Decoder： Decoder也是 $N = 6$ 层，除了每个 Encoder 中的两个子层外，Decoder 还插入了第三个子层，该子层对 Encoder Stack 的输出执行多头注意力机制。修改了 Decoder Stack 中的自注意子层，确保对位置 $i$ 的预测只能依赖于小于位置 $i$ 的已知输出。

Attention

Self-Attention

输入包含维度 $d_k$ 的 Query 和 Key 以及维度为 $d_v$ 的 Value.
Self-Attention
$\tag{2} \textmd {Attention}(Q,K,V)=\textmd{softmax}(\frac {QK^T} {\sqrt{d_k}})V.$ 其中的 $\frac 1 {\sqrt {d_k}}$ 为尺度因子。对于输入序列中每个单词之间的相关性得分进行归一化，归一化的目的主要是为了训练时梯度能够稳定，即为了防止维数过高时的值过大导致softmax函数反向传播时发生梯度消失。两种最常用的 Attention 函数为 additive attention 和 dot-product (multi-plicative) attention.

不同的 $X^i$ 分享了同一个 $W^Q、W^K、W^V$ 。通过这个操作， $a^i$ 之间已经发生了某种程度上的信息交换。获取到不同的 $Q_i 、K_i 、V_i$ ，从而获取不同 tokens 的 Attention。

Self-Attention通过计算一个注意力权重矩阵，来表征输入序列中每个 token 与其他 token 之间的关系。这个注意力权重矩阵可以看作是每个 token 对其他 token 的重要性权重。通过将注意力权重矩阵与输入序列的嵌入向量进行加权求和(权重即Sotmax())，可以融合各个 token 之间的信息。

具体来说，Self-Attention的计算过程如下：
1.将输入序列中每个token的嵌入向量分别作为查询向量（query）、键向量（key）和值向量（value）。
2.计算查询向量与键向量之间的相似度得分，一般采用点积或双线性形式进行计算。
3.对相似度得分进行归一化，得到注意力权重矩阵，它表示每个token对其他token的重要性权重。
4.将注意力权重矩阵与值向量进行加权求和，得到每个token融合了其他token信息的表示。
5.重复以上步骤多次，每次使用不同的查询、键、值来融合不同的信息。

通过Self-Attention机制，模型可以同时考虑输入序列中每个token与其他token之间的关系，并将这些关系进行融合，从而获取全局的上下文信息。 这使得模型能够捕捉到长距离依赖和语义关联，从而提高了模型的表达能力和性能。

Multi-Attention

如果使用不同的 $W^Q、W^K、W^V$ 就能得到不同的 $Q 、 K 、 V$ ， Multi-headed Attention就是指用了很多个不同的 $W^Q、W^K、W^V$ .

$\tag{3} \textmd{MultiHead}(Q,K,V)=\textmd{Concat}(head_1,...,head_h)W^O\\ \textmd{where} \space head_i=\textmd{Attention}(QW_i^Q,KW_i^K,VW_i^V).$
在这里插入图片描述

Multi-Head Attention（多头注意力）是Self-Attention机制在Transformer模型中的一种变体，它用于增强模型对不同关系和特征的建模能力。

在Self-Attention中，通过计算注意力权重矩阵来融合各个token之间的信息。而在Multi-Head Attention中，模型会同时使用多个注意力头（attention head）来进行注意力计算。

具体来说，Multi-Head Attention通过将输入的嵌入向量分别经过多个独立的查询、键和值投影矩阵来产生多组查询向量、键向量和值向量。然后，每个注意力头都会对这些查询、键和值进行自注意力计算，得到多个注意力权重矩阵。最后，这些注意力权重矩阵会被拼接起来，并经过另一个投影矩阵进行线性变换，得到最终的注意力输出。

通过使用多个注意力头，Multi-Head Attention能够并行地学习不同的关系和特征表示。每个注意力头可以关注输入序列中不同的相关性，从而提高了模型的表达能力和泛化能力。每个头独立地学习权重，使得模型能够在不同的表示子空间中进行信息融合，捕捉不同的语义特征。

前馈网络

$\tag{4}\textmd{FFN}(x)=\max (0,xW_1+b_1)W_2+b_2$

Embeding

输入模型的整个 Embedding 是Word Embedding 与 Positional Embedding 直接相加之后的结果。
Encoder输入的是单词的embedding：对其进行随机初始化（当然也可以选择Pre-trained的结果），但设为Trainable。这样在training过程中不断地对embeddings进行改进。即End2End训练方式。

位置编码

由于 transformer 模型不包含递归和卷积，为了使模型能够利用序列的顺序，必须注入一些关于 tokens 在序列中的相对或绝对位置的信息。因此，在 Encoder Stack 和 Decoder Stack 底部的输入 Embeding 中添加“位置编码”。
使用不同频率的正弦和余弦函数： $\tag{5}PE_{(pos,2i)}=\sin(pos/10000^{2i/d_{model}})\\ PE_{(pos,2i+1)}=\cos (pos/10000^{2i/d_{model}})$ 其中 $p os$ 是位置， $i$ 是维度。位置编码的每个维对应于一个正弦曲线。波长从 $2 π$ 到 $10000 \cdot 2 π$ 呈几何级数。
根据公式 $\sin (\alpha+\beta)=\sin\alpha \cos\beta+\cos\alpha\sin\beta$ 以及 $\cos (\alpha+\beta)=\cos \alpha\cos\beta-\sin\alpha\sin\beta$ ，对于任何固定的偏移 $k$ ， $PE_{pos+k}$ 可以表示为 $PE_{pos}$ 的一个线性函数。