一：高斯函数

（1）定义

高斯函数：是一种常见的连续函数，通常用符号 $G(x)$ 表示。它可以用下面的公式定义

$$G(x)=\frac{1}{\sigma \sqrt{2\pi }}{e}^{-\frac{x^2}{2{\sigma }^2}}$$

其中，$x$ 是自变量，$\sigma$ 是一个正实数，表示高斯函数的标准差。高斯函数具有以下性质：

• 高斯函数是一个偶函数，即 $G(-x)=G(x)$
• 高斯函数的曲线呈钟形，且在 $x=0$ 处取得峰值。标准差 $\sigma$ 越小，高斯函数的峰值越高，曲线越陡峭；标准差 $\sigma$ 越大，高斯函数的峰值越低，曲线越平缓
• 高斯函数的面积为 $1$，即 ${\int }_{-\infty }^{\infty }G(x)dx=1$
• 当 $\sigma$ 趋近于 $0$ 时，高斯函数的峰值趋近于无穷大，曲线变得越来越陡峭，趋近于一个 $\delta$ 函数。$\delta$ 函数是一个类似于脉冲的函数，当自变量等于 $0$ 时，函数值无限大，而在其他位置上函数值都为 $0$

以下是高斯函数和其一阶导数形式

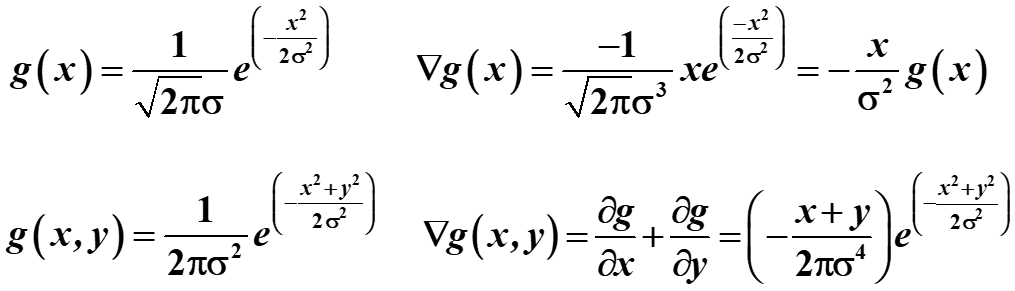
以下是高斯函数二阶导数形式

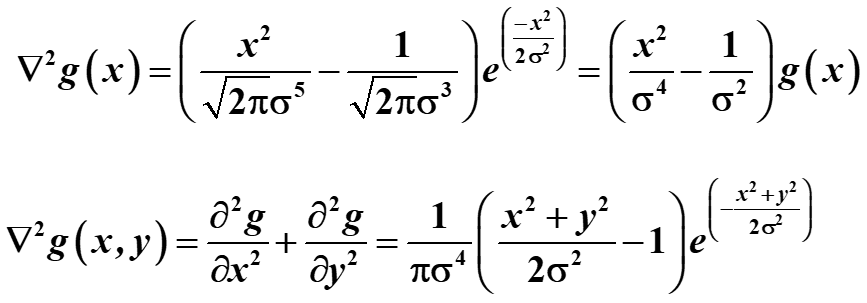
（2）特点

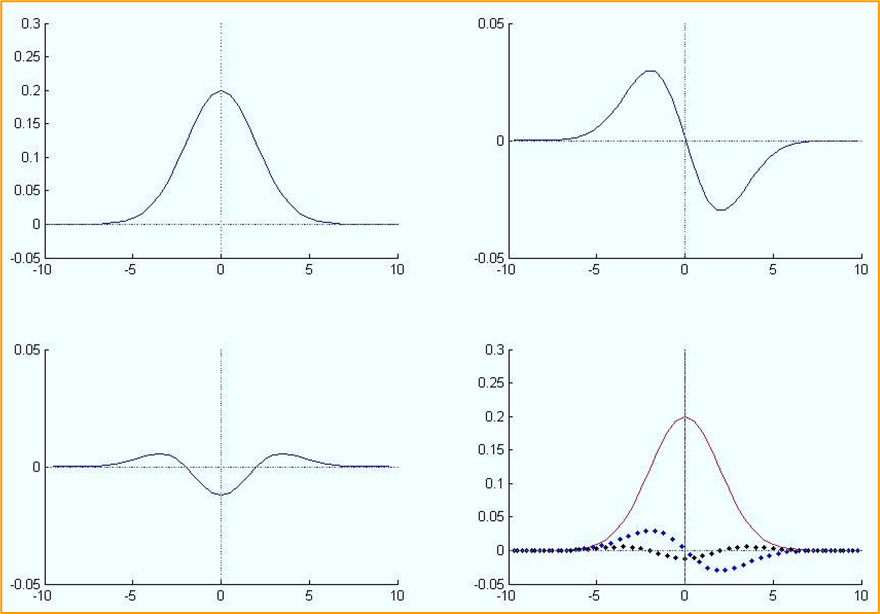
• 随着远离原点，权值逐渐减小到零，表明离中心较近的图像值比远处的更重要
• 标准差$\sigma$决定邻域范围，总权值的95％包含在$2\sigma$的中间范围内
• 二阶导数具有光滑的中间突出部分，函数值为负；两个光滑的侧边突出部分，值为正
• 零交叉位于$-\sigma$和$+\sigma$处，与$g(x)$的拐点和$g^{\prime }(x)$的极值点对应
• 1D形式绕垂直轴旋转得各向同性的2D函数形式（在任意过原点的切面上具有相同的1D高斯截面），其二阶导数形式好像一个宽边帽或称为墨西哥草帽
• 从数学推导上，帽子的空腔口沿$z=g(x,y)$轴向上，在显示和滤波应用中空腔口一般朝下，即中间突起的部分为正，帽边为负

二：LOG算子

（1）定义

LOG算子：Marr用高斯函数先对图像作平滑，然后用拉普拉斯算子检测边缘，简称LOG滤波器

$$\mathrm{LoG}(x,y)=\frac{1}{\pi {\sigma }^4}\left[1-\frac{x^2+y^2}{2{\sigma }^2}\right]e^{-\frac{x^2+y^2}{2{\sigma }^2}}$$

LOG算子可以看作是将高斯函数和拉普拉斯算子（即二阶导数算子）结合在一起，因此它的输出是原始图像的拉普拉斯变换与高斯滤波的结果。它可以用来检测图像中的边缘和角点等特征。将$g$与图像函数$f$卷积，得到一个平滑的图像函数，对该函数做拉普拉斯运算，提取边缘

可以证明

$${\nabla }^2[f(x,y)\ast g(x,y)]=f(x,y)\ast {\nabla }^{2}g(x,y)$$

$${\nabla }^{2}g(x,y)=\frac{{\partial }^{2}g}{\partial x^2}+\frac{{\partial }^{2}g}{\partial y^2}=\frac{1}{\pi {\sigma }^4}\left(\frac{x^2+y^2}{2{\sigma }^2}-1\right)\exp \left(-\frac{x^2+y^2}{2{\sigma }^2}\right)$$

${\nabla }^{2}g(x,y)$为LOG滤波器，也称为Marr-Hildrech算子

• $\sigma$为尺度因子，大的值可以用来检测模糊边缘，小的值可以用来检测聚焦良好的图像细节

LOG算子的形状如下图所示

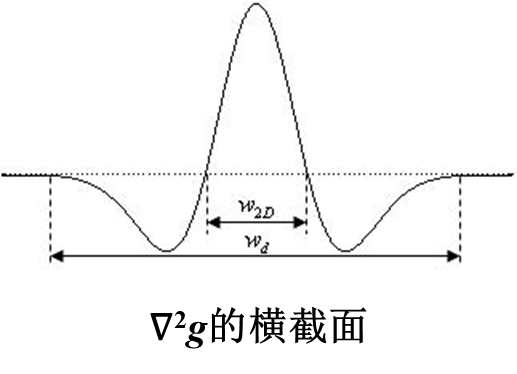
滤波器的大小由$\sigma$的数值或等价地由${\omega }_{2D}$的数值来确定。为了不使函数被过分地截短，应在足够大的窗口内作计算，窗口宽度通常取为$\omega \ge 3.6{\omega }_{2D}$

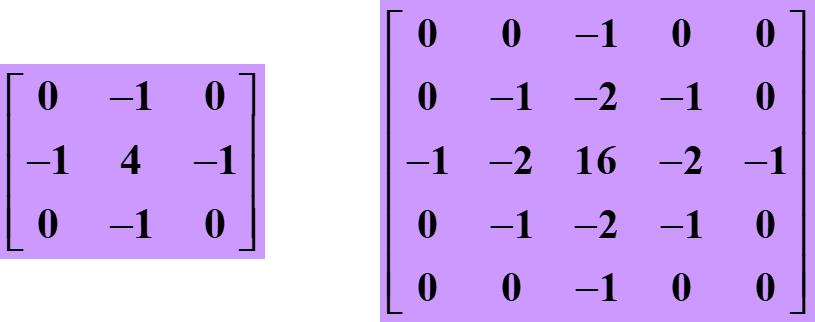
当$\sigma$取不同值时，对应不同模板

（2）程序

---

matlab实现：

Image=im2double(rgb2gray(imread('lotus.jpg')));
figure,imshow(Image),title('原图像');
H=fspecial('laplacian',0);
R=imfilter(Image,H);
edgeImage=abs(R);
figure,imshow(edgeImage),title('Laplacian梯度图像');
H1=[0 -1 0;-1 5 -1;0 -1 0];
sharpImage=imfilter(Image,H1);
figure,imshow(sharpImage),title('Laplacian锐化图像');

Python实现：

import cv2
import matplotlib.pyplot as plt
import numpy as np

# 读入图像
Image = cv2.imread('lotus.jpg')
Image = cv2.cvtColor(Image, cv2.COLOR_BGR2GRAY)
Image = Image.astype(np.float64) / 255.0

# 显示原图像
plt.imshow(Image, cmap='gray')
plt.title('原图像')
plt.show()

# 计算Laplacian梯度图像
H = np.array([[0, 1, 0], [1, -4, 1], [0, 1, 0]], dtype=np.float64)
R = cv2.filter2D(Image, -1, H)
edgeImage = np.abs(R)

# 显示Laplacian梯度图像
plt.imshow(edgeImage, cmap='gray')
plt.title('Laplacian梯度图像')
plt.show()

# 计算Laplacian锐化图像
H1 = np.array([[0, -1, 0], [-1, 5, -1], [0, -1, 0]], dtype=np.float64)
sharpImage = cv2.filter2D(Image, -1, H1)

# 显示Laplacian锐化图像
plt.imshow(sharpImage, cmap='gray')
plt.title('Laplacian锐化图像')
plt.show()

三：Canny算子

（1）最优边缘检测

最优边缘检测：是指在所有边缘检测算法中，能够获得最佳边缘检测结果的算法。然而，没有一种边缘检测算法能够在所有情况下都表现最优，因为不同的算法适用于不同类型的图像和不同的应用场景。因此，我们需要根据具体情况选择最适合的边缘检测算法。最优边缘检测的三个主要评价标准

• 低错误率：标识出尽可能多的实际边缘，同时尽可能的减少噪声产生的误报。
• 对边缘的定位准确：标识出的边缘要与图像中的实际边缘尽可能接近。
• 最小响应：图像中的边缘最好只标识一次，并且可能存在的图像噪声部分不应标识为边缘

（2）Canny算子

Canny算子：是一种广泛使用的边缘检测算法，由John Canny在1986年提出。它可以检测出具有低误差率和高定位精度的边缘，并被认为是目前最优秀的边缘检测算法之一。算法步骤如下

• 去噪：首先，应该对图像进行高斯滤波，以去除噪声
• 计算梯度：然后，通过使用Sobel算子计算图像的梯度，以检测出边缘的强度和方向
• 非极大值抑制：接下来，在梯度方向上进行非极大值抑制，以消除较小的边缘响应和边缘的宽度，保留梯度方向上的局部最大值
• 双阈值处理：然后，应该根据梯度值进行双阈值处理，将像素点分为强边缘、弱边缘和非边缘三类
• 边缘连接：最后，应该通过连接强边缘像素点和与其相邻的弱边缘像素点，形成完整的边缘。连接边缘的过程可以使用基于深度优先搜索或者基于连通性分析的方法

Canny算子的优点在于，它具有良好的边缘连接性、单一响应和低误差率。缺点在于计算量较大。此外，Canny算子对参数的选择非常敏感，需要根据具体应用场景进行调整

（3）程序

---

matlab实现：

Image=im2double(rgb2gray(imread('lotus.jpg')));
figure,imshow(Image),title('原图像');
BW= edge(Image,'canny');
figure,imshow(BW),title('Canny边缘检测');

Python实现：

Image=im2double(rgb2gray(imread('lotus.jpg')));
figure,imshow(Image),title('原图像');
BW= edge(Image,'canny');
figure,imshow(BW),title('Canny边缘检测');