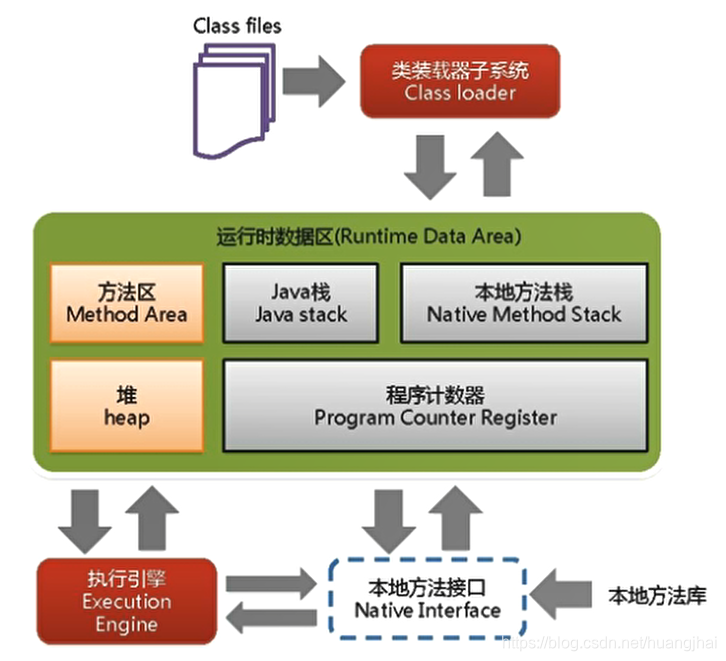
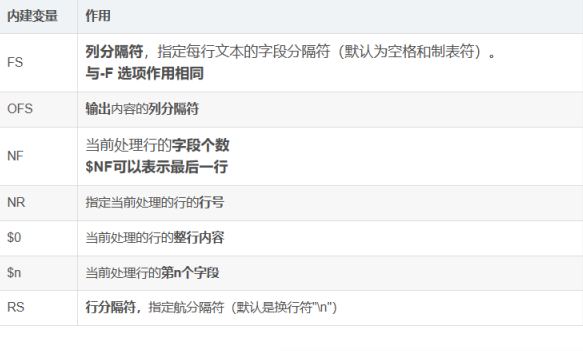
AVL tree介绍

AVL的全称是：Adelson-Velsky-Landis，是发明这种高度平衡二叉树的人名的缩写，AVL tree是一种优化了的搜索二叉树。

这是二叉排序树会存在的一个问题，先看案例:

给定一个数列为{1,2,3,4,5,6}，将这个数列转换为二叉排序树

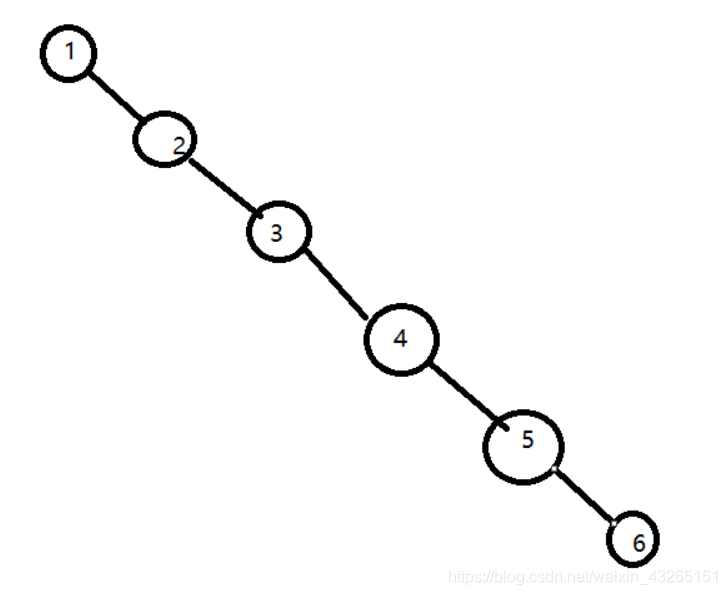
根据二叉排序树的性质可以得到这样的二叉排序树，这样的树有这么几个问题:

• 左子树全部为空，从形式上看更像是一个链表
• 对于二叉树的插入速度没有影响
• 查询速度明显降低（需要依次比较），不能发挥出二叉排序树的特点

由于这样的情况，便可以引出平衡二叉树，平衡二叉树就可以完美的解决这个问题

• 平衡二叉树也叫二叉搜索树又被称为AVL树，可以保证拥有较高的查询效率
• AVL树具有以下特点，它是一颗空树，或它的左右两个子树的高度差（平衡因子）的绝对值不超过1，并且左右两个子树都是一颗平衡二叉树。

1.举例说明

二叉树的存储结构

顺序存储

        二叉树的顺序存储采用的存储结构是顺序表（数组）。但是只有完全二叉树才可以使用顺序表存储。如果想要存储普通二叉树，我们就要先将普通二叉树转换为完全二叉树。

        普通二叉树转完全二叉树的方法很简单，只需给二叉树额外添加一些节点，将其"拼凑"成完全二叉树即可。

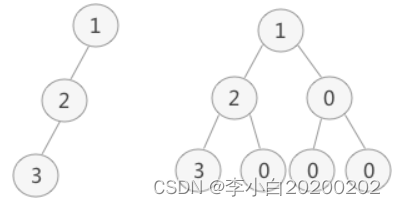
上图中，左侧是普通二叉树，右侧是转化后的完全（满）二叉树。
解决了二叉树的转化问题，接下来学习如何顺序存储完全（满）二叉树。
完全二叉树的顺序存储，仅需从根节点开始，按照层次依次将树中节点存储到数组即可。

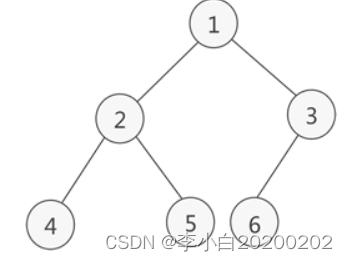
完全二叉树在数组的存储状态：

 

存储由普通二叉树转化来的完全二叉树也是如此：

从顺序表中还原完全二叉树也很简单。我们知道，完全二叉树具有这样的性质，将树中节点按照层次并从左到右依次标号（1,2,3,...），若节点 i 有左右孩子，则其左孩子节点为 2*i，右孩子节点为 2*i+1。此性质可用于还原数组中存储的完全二叉树。

链式存储

  因为并不是每个二叉树都是完全二叉树，所以普通二叉树在转换成完全二叉树时，会徒增很多空结点，这些空结点还都需要存储在数组中，这无疑对内存空间造成了大量的浪费。

        所以。树的存储我们经常采用的是链式存储结构。

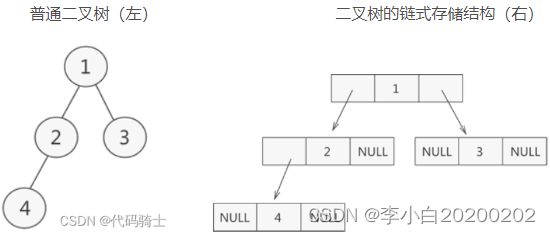
采用链式存储二叉树时，其节点结构由 3 部分构成：

• 指向左孩子节点的指针（Lchild）；
• 节点存储的数据（data）；
• 指向右孩子节点的指针（Rchild）；

如图：

表示结点结构的C语言代码： 

 typedef struct BiTNode{

 TElemType data;//数据域

 struct BiTNode *lchild,*rchild;//左右孩子指针

 struct BiNode *parent;//父结点指针

 }BiTNode,*Bi

通常情况下也可不写父结点指针，这是为了我们方便找到结点的父结点而写的。

  

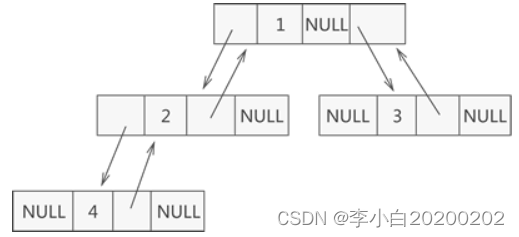
这样的链表结构，通常称为三叉链表。

查找二叉树

 二叉查找树（Binary Search Tree）,又被称为二叉搜索树。设x为二叉树中的一个节点，x节点包含关键字Key，节点x的Key值记为Key[x]。如果y是x的左子树中的一个节点，则Key[y]<=Key[x]；如果y是x的有子树的一个节点，则Key[y]>=Key[x]。
  

查找规则

 1、若任意节点的左子树不空，则左子树上所有的值均小于根节点的值

 2、若任意节点的右子树不空，则右子树上所有节点的值均大于根节点的值（更大于左子树上的值）

3、任意节点的左、右子树也分别为二叉查找树

4、没有键值相等的节点
 

深度为k的二叉树最少有k个节点，最多有2的k次方减1个节点。

最少：斜二叉树，已经退化为线性结构。
最多：每层的节点个数为2的k次方，根目录为0层，即K的值为0。