分配训练集&Validation数量

validation_size = training_size * validation_ratio / (1 - validation_ratio)

training_size = 219
validation_ratio = 0.2
validation_size = 219*0.2/(1-0.2)

如果你有 346 张验证图像，使用 k=5 的交叉验证方法，你可以将这些图像分成 5 个不同的折叠（fold），每个折叠包含 69 或 70 张图像。

平均分配图像的方法：
num_images_per_fold = len(val_images) // num_folds

from sklearn.model_selection import KFold

# 假设你有 291 个训练图像和 55 个验证图像
train_images = range(291)
valid_images = range(291, 291+55)

# 将训练图像分成五个部分
kf = KFold(n_splits=5, shuffle=True)
for fold, (train_idx, valid_idx) in enumerate(kf.split(train_images)):
    # 选择一个部分作为验证集，其余部分作为训练集
    train_images_fold = [train_images[i] for i in train_idx]
    valid_images_fold = [train_images[i] for i in valid_idx]

    # 在每次交叉验证中，使用训练集进行训练，并使用验证集进行验证
    # TODO: 训练和验证模型

    # 记录模型的性能指标
    # TODO: 记录模型性能指标

# 将五个结果的平均值作为模型的性能指标
# TODO: 计算模

数据集读取

读取全部文件夹

p = Path(p) # p = WindowsPath('E:/data/helmet_head/train')
glob.glob(str(p / '**' / '*.*'), recursive=True)

这行 Python 代码使用了 pathlib 模块中的 WindowsPath 类来创建一个 Windows 路径对象 p，表示了一个名为 train 的目录，该目录位于 E:/data/helmet_head/ 目录下。接下来，使用 glob 函数来获取该目录及其所有子目录中的所有文件（包括子目录中的文件）。

p / '**' / '*.*' 表示将 p 对象的路径添加上 '**'（表示所有子目录），然后再添加上 '*.*'（表示所有类型的文件）路径，得到一个包含通配符的字符串路径。这个字符串路径会被转换为一个 WindowsPath 对象并传递给 glob 函数。
glob(str(p / '**' / '*.*'), recursive=True) 表示使用 glob 函数获取符合给定路径模式的文件列表。recursive=True 表示要递归地查找子目录中的文件。

替换路径

x = 'E:\\data\\helmet_head\\train\\collect20120420\\JPEGImages\\000000.jpg'
sa = '\\JPEGImages\\'
sb = '\\Annotations\\'
sb.join(x.rsplit(sa, 1))

将指定路径 x 中的子目录名称 ‘JPEGImages’ 替换为 ‘Annotations’

x.rsplit(sa, 1) 使用 rsplit 函数将路径 x 按照指定的子目录名称 ‘JPEGImages’ 进行分割，并将分割结果作为一个列表返回。其中，sa 是分割字符串，1 表示只分割一次，即只分割最后一次出现的位置。
x.rsplit(sa, 1) 的结果为：
[‘E:\data\helmet_head\train\collect20120420’, ‘000000.jpg’]。

'\\Annotations\\'.join(x.rsplit(sa, 1)) 使用 ‘\Annotations\’ 字符串将分割后的列表中的元素连接起来，得到一个新的路径。这个路径将原路径中的子目录名称 ‘JPEGImages’ 替换为 ‘Annotations’。
‘\Annotations\’.join(x.rsplit(sa, 1)) 的结果为：

'E:\data\helmet_head\train\collect20120420\\Annotations\\000000.jpg’

loss weight

Pytorch: BCEWithLogitsLoss

YOLO v5 中的loss weight 在data/hyp/scratch.yaml 中的cls_pw，同时 obj_pw 也可以使用同样的vector
通过train.py 中：

model.class_weights = labels_to_class_weights(dataset.labels, nc).to(device) * nc  # attach class weights

weights = np.bincount(classes, minlength=nc)
weights[weights == 0] = 1  # replace empty bins with 1
weights = 1 / weights  # number of targets per class
weights /= weights.sum()

得到3个种类在数量上应该受到的提高为： tensor([0.12096, 2.43440, 0.44464])
其中数字越大的代表数据量越少

target = torch.ones([4,3,8,8], dtype=torch.float32)
output = torch.full([4,3,8,8], 1.5)
pos_weight = torch.ones([3,8,8])
criterion = torch.nn.BCEWithLogitsLoss(pos_weight=pos_weight)
criterion(output, target)

这里的pos_weight = torch.ones([3,8,8]) 一定确保倒数的维度和output/target 相同

初始的cls_pw 是一个scalar, 如下：

target = torch.ones([4,3,8,8], dtype=torch.float32)
output = torch.full([4,3,8,8], 1.5)
pos_weight = torch.ones([1])
criterion = torch.nn.BCEWithLogitsLoss(pos_weight=pos_weight)
criterion(output, target)

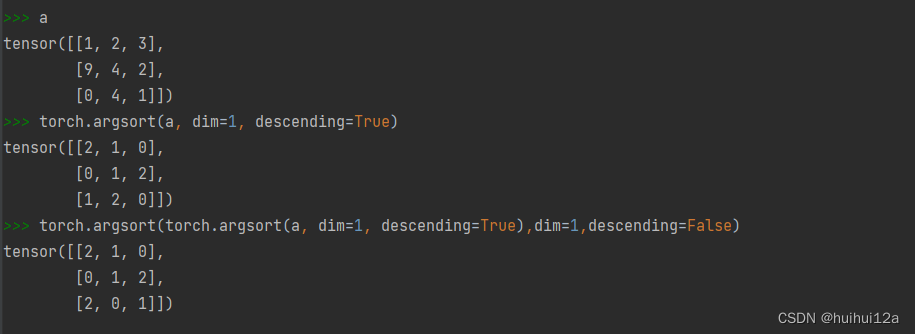
NMS

以下是torch 版的 NMS，代替了torchvision.ops.nms(boxes, scores, iou_thres)

def nms(bboxes, scores, iou_thresh=0.5):
    _, order = scores.sort(0, descending=True)
    keep = []

    while order.numel() > 0:
        if order.numel() == 1:  # 保留框只剩一个
            i = order.item()
            keep.append(i)
            break
        else:
            i = order[0].item()  # 保留scores最大的那个框box[i]
            keep.append(i)

        iou = bbox_iou_new(bboxes[i], bboxes[order[1:]]).squeeze()

        idx = (iou <= iou_thresh).nonzero().squeeze()  # 注意此时idx为[N-1,] 而order为[N,]
        if idx.numel() == 0:
            break
        order = order[idx + 1]  # 修补索引之间的差值

    return keep

以下是计算bbox的，这个function 被用于替换 NMS中计算IOU。这样做可以帮助做些关于IOU相关的ablation 分析

def bbox_iou_new(box1, box2, GIoU=False, DIoU=False, CIoU=False, SIoU=False, EIoU=False, Focal=True, eps=1e-7):
    # Returns Intersection over Union (IoU) of box1(1,4) to box2(n,4)

    b1_x1, b1_y1, b1_x2, b1_y2 = box1.chunk(4, -1)
    b2_x1, b2_y1, b2_x2, b2_y2 = box2.chunk(4, -1)
    w1, h1 = b1_x2 - b1_x1, (b1_y2 - b1_y1).clamp(eps)
    w2, h2 = b2_x2 - b2_x1, (b2_y2 - b2_y1).clamp(eps)

    # Intersection area
    inter = (b1_x2.minimum(b2_x2) - b1_x1.maximum(b2_x1)).clamp(0) * \
            (b1_y2.minimum(b2_y2) - b1_y1.maximum(b2_y1)).clamp(0)

    # Union Area
    union = w1 * h1 + w2 * h2 - inter + eps

    # IoU
    iou = inter / union
    if CIoU or DIoU or GIoU or EIoU:
        cw = b1_x2.maximum(b2_x2) - b1_x1.minimum(b2_x1)  # convex (smallest enclosing box) width
        ch = b1_y2.maximum(b2_y2) - b1_y1.minimum(b2_y1)  # convex height
        if CIoU or DIoU or EIoU:  # Distance or Complete IoU https://arxiv.org/abs/1911.08287v1
            c2 = cw ** 2 + ch ** 2 + eps  # convex diagonal squared
            rho2 = ((b2_x1 + b2_x2 - b1_x1 - b1_x2) ** 2 + (b2_y1 + b2_y2 - b1_y1 - b1_y2) ** 2) / 4  # center dist ** 2
            if CIoU:  # https://github.com/Zzh-tju/DIoU-SSD-pytorch/blob/master/utils/box/box_utils.py#L47
                v = (4 / math.pi ** 2) * (torch.atan(w2 / h2) - torch.atan(w1 / h1)).pow(2)
                with torch.no_grad():
                    alpha = v / (v - iou + (1 + eps))
                return iou - (rho2 / c2 + v * alpha)  # CIoU
            elif EIoU:
                rho_w2 = ((b2_x2 - b2_x1) - (b1_x2 - b1_x1)) ** 2
                rho_h2 = ((b2_y2 - b2_y1) - (b1_y2 - b1_y1)) ** 2
                cw2 = cw ** 2 + eps
                ch2 = ch ** 2 + eps
                if Focal:
                    gamma = 0.5
                    return (iou - (rho2 / c2 + rho_w2 / cw2 + rho_h2 / ch2)) * torch.pow(inter / (union + eps), gamma).mean()  # Focal_EIou
                return iou - (rho2 / c2 + rho_w2 / cw2 + rho_h2 / ch2)
            return iou - rho2 / c2  # DIoU
        c_area = cw * ch + eps  # convex area
        return iou - (c_area - union) / c_area  # GIoU https://arxiv.org/pdf/1902.09630.pdf
    elif SIoU:
        # SIoU Loss https://arxiv.org/pdf/2205.12740.pdf
        s_cw = (b2_x1 + b2_x2 - b1_x1 - b1_x2) * 0.5 + eps
        s_ch = (b2_y1 + b2_y2 - b1_y1 - b1_y2) * 0.5 + eps
        sigma = torch.pow(s_cw ** 2 + s_ch ** 2, 0.5)
        sin_alpha_1 = torch.abs(s_cw) / sigma
        sin_alpha_2 = torch.abs(s_ch) / sigma
        threshold = pow(2, 0.5) / 2
        sin_alpha = torch.where(sin_alpha_1 > threshold, sin_alpha_2, sin_alpha_1)
        angle_cost = torch.cos(torch.arcsin(sin_alpha) * 2 - math.pi / 2)
        rho_x = (s_cw / cw) ** 2
        rho_y = (s_ch / ch) ** 2
        gamma = angle_cost - 2
        distance_cost = 2 - torch.exp(gamma * rho_x) - torch.exp(gamma * rho_y)
        omiga_w = torch.abs(w1 - w2) / torch.max(w1, w2)
        omiga_h = torch.abs(h1 - h2) / torch.max(h1, h2)
        shape_cost = torch.pow(1 - torch.exp(-1 * omiga_w), 4) + torch.pow(1 - torch.exp(-1 * omiga_h), 4)
        return iou - 0.5 * (distance_cost + shape_cost)
    return iou  # IoU

BBox_IOU

CIOU 弥补了 GIOU 只考虑重合不考虑临近但也可用的框。但是CIOU中的那几个criteria 依然还有缺点:
在这里插入图片描述

v 不太靠谱
- 如果 w, h 的量级为 ground-truth 的整倍数，那么v 为 0 （无效，一样大才是想要的，但不是倍数大）比如 K倍：
- $w= kw^{gt}, h = kw^{gt}$ $\frac{4}{\pi ^2}(arctan \frac{w^{gt}}{h^{gt}}-arctan\frac{kw^{gt}}{kh^{gt}})^2 = 0$
还是 v 的这一步在gradient 这里引起的不靠谱
- w, h 会有相反的符号, 当 w 和 h 都比 ground truth 大/小时，两个量按理也应该同时扩大/缩小。
- 符号导致对w,h 处理不公。
- 细节原因：
  做partial gradient 后，w, h 会因为 V中原本用来算宽高比之差的地方，导致各自在gradient 时，遭遇不公
  这里的v 如果不放进训练过程，倒也还是make sense, 可以看作是宽高比的 norm-2 的计算。但放进训练，就要搞gradient，也就是搞partial gradient，就从🆗到不太行了。