文章目录
- (简单)203. 移除链表元素
- (中等)707. 设计链表
- (简单)206. 反转链表
- (中等)24. 两两交换链表中的节点
- (中等)19. 删除链表的倒数第 N 个结点
- (简单)面试题 02.07. 链表相交
- (*中等)142. 环形链表 II
(简单)203. 移除链表元素
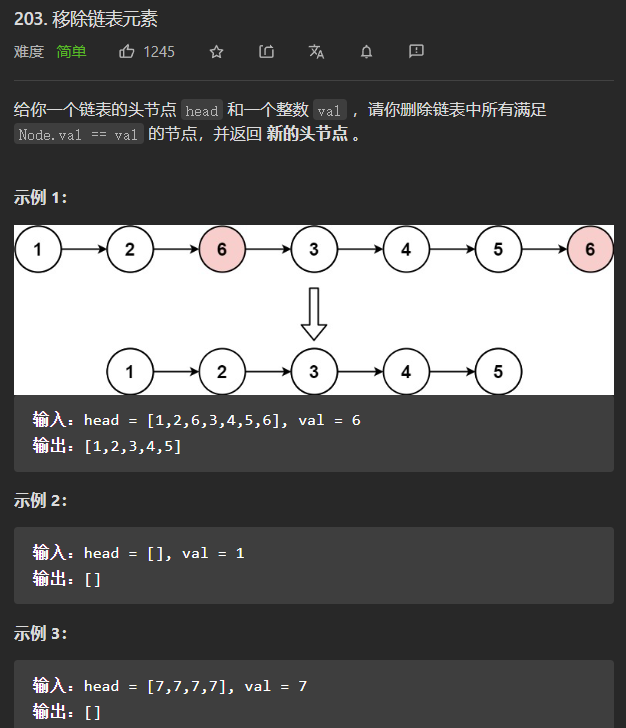
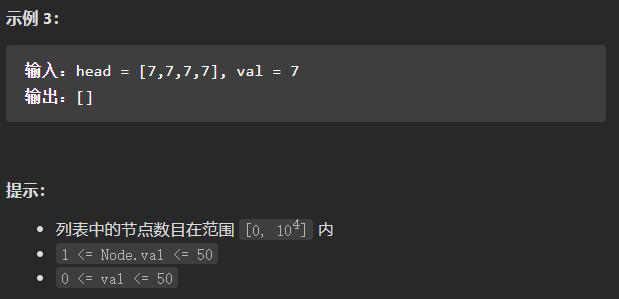
我的思路:
要想移除链表中的某一个节点,那么就需要知道该节点的前一个节点。
其次是如果要删除的节点就是第一个,那么就先处理第一个节点就是要删除节点的情况。
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode() {}
* ListNode(int val) { this.val = val; }
* ListNode(int val, ListNode next) { this.val = val; this.next = next; }
* }
*/
class Solution {
public ListNode removeElements(ListNode head, int val) {
if (head == null) {
return null;
}
while (head != null && head.val == val) {
head = head.next;
}
if (head == null) {
return null;
}
ListNode pre = head;
ListNode p = head.next;
while (p != null) {
if (val == p.val) {
pre.next = p.next;
} else {
pre = p;
}
p = p.next;
}
return head;
}
}
官方思路,迭代
使用迭代的方法删除链表中所有节点值等于特定值的节点。
用temp表示当前节点。如果temp的下一个节点不为空且下一个节点的节点值等于给定的val,则需要删除下一个节点。删除下一个节点可以通过以下做法实现:
temp.next = temp.next.next;
如果temp的下一个节点的节点值不等于给定的val,则保留下一个节点,将temp移动到下一个节点即可。
当temp的下一个节点为空时,链表遍历结束,此时所有节点值等于val的节点都被删除。
具体实现方面,由于链表的头节点head有可能需要被删除,因此创建哑节点preHead,令preHead.next=head,初始化p=preHead,然后遍历链表进行删除操作。最终返回preHead.next即为删除操作后的头节点。
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode() {}
* ListNode(int val) { this.val = val; }
* ListNode(int val, ListNode next) { this.val = val; this.next = next; }
* }
*/
class Solution {
public ListNode removeElements(ListNode head, int val) {
if (head == null) {
return null;
}
ListNode preHead = new ListNode(-1);
preHead.next = head;
ListNode p = preHead;
while (p.next != null) {
if (p.next.val == val) {
p.next = p.next.next;
} else {
p = p.next;
}
}
return preHead.next;
}
}
(中等)707. 设计链表
设计一个链表的节点类,然后编写代码即可
class MyLinkedList {
private ListNode preHead;
public MyLinkedList() {
preHead = new ListNode(-1);
}
public int get(int index) {
ListNode p = preHead.next;
int i = 0;
while (p != null && index != i) {
p = p.next;
i++;
}
if (p != null) {
return p.val;
} else {
return -1;
}
}
public void addAtHead(int val) {
ListNode newNode = new ListNode(val);
newNode.next = preHead.next;
preHead.next = newNode;
}
public void addAtTail(int val) {
ListNode newNode = new ListNode(val);
ListNode p = preHead;
while (p.next != null) {
p = p.next;
}
p.next = newNode;
}
public void addAtIndex(int index, int val) {
int i = 0;
ListNode q = preHead;
ListNode p = preHead.next;
ListNode newNode = new ListNode(val);
while (p != null && index != i) {
p = p.next;
q = q.next;
i++;
}
if (p != null) {
newNode.next = p;
q.next = newNode;
} else {
if (i == index) {
q.next = newNode;
}
}
}
public void deleteAtIndex(int index) {
ListNode q = preHead;
ListNode p = preHead.next;
int i = 0;
while (p != null && index != i) {
q = q.next;
p = p.next;
i++;
}
if (p != null) {
q.next = p.next;
}
}
}
class ListNode {
int val;
ListNode next;
public ListNode(int val) {
this.val = val;
}
}
/**
* Your MyLinkedList object will be instantiated and called as such:
* MyLinkedList obj = new MyLinkedList();
* int param_1 = obj.get(index);
* obj.addAtHead(val);
* obj.addAtTail(val);
* obj.addAtIndex(index,val);
* obj.deleteAtIndex(index);
*/
官方思路,方法一:单向链表
实现单向链表,即每个节点仅存储本身的值和后继节点,除此之外,还需要一个哨兵(sentinel)节点作为头节点,和一个size参数保存有效节点数。如下图所示。
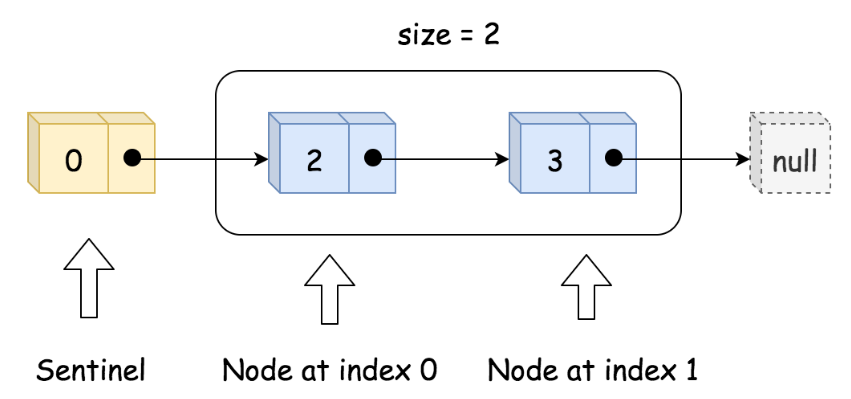
初始化时,只需创建头节点head和size即可。
实现get(index)时,先判断有效性,再通过循环来找到对应的节点的值。
官方代码,相较于我自己的代码,区别在于加入了size熟悉,方便判断参数index是否合法
class MyLinkedList {
ListNode preHead;
int size;
public MyLinkedList() {
size = 0;
preHead = new ListNode(-1);
}
public int get(int index) {
if (index < 0 || index >= size) {
return -1;
}
ListNode cur = preHead;
for (int i = 0; i <= index; i++) {
cur = cur.next;
}
return cur.val;
}
public void addAtHead(int val) {
addAtIndex(0, val);
}
public void addAtTail(int val) {
addAtIndex(size, val);
}
public void addAtIndex(int index, int val) {
if (index < 0 || index > size) {
return;
}
size++;
ListNode q = preHead;
for (int i = 0; i < index; i++) {
q = q.next;
}
ListNode newNode = new ListNode(val);
newNode.next = q.next;
q.next = newNode;
}
public void deleteAtIndex(int index) {
if (index < 0 || index >= size) {
return;
}
size--;
ListNode cur = preHead;
for (int i = 0; i < index; i++) {
cur = cur.next;
}
cur.next = cur.next.next;
}
}
class ListNode {
int val;
ListNode next;
public ListNode(int val) {
this.val = val;
}
}
/**
* Your MyLinkedList object will be instantiated and called as such:
* MyLinkedList obj = new MyLinkedList();
* int param_1 = obj.get(index);
* obj.addAtHead(val);
* obj.addAtTail(val);
* obj.addAtIndex(index,val);
* obj.deleteAtIndex(index);
*/
官方思路,方法二:双向链表
实现双向链表,即每个节点都要存储本身的值,后继节点和前驱节点。除此之外,需要一个哨兵节点作为头节点head和一个哨兵节点作为尾节点tail。仍然需要一个size参数保存有效节点数。
双向链表的代码比单向链表复杂一点,因为总是要判断那一边离要操作的index的位置较近
class MyLinkedList {
ListNode head;
ListNode tail;
int size;
public MyLinkedList() {
size = 0;
head = new ListNode(-1);
tail = new ListNode(-1);
head.next = tail;
tail.prev = head;
}
public int get(int index) {
if (index < 0 || index >= size) {
return -1;
}
ListNode cur;
//判断,距离头节点近,还是尾节点近
if (index < size - index - 1) {
cur = head;
for (int i = 0; i <= index; i++) {
cur = cur.next;
}
} else {
cur = tail;
for (int i = size; i > index; i--) {
cur = cur.prev;
}
}
return cur.val;
}
public void addAtHead(int val) {
addAtIndex(0, val);
}
public void addAtTail(int val) {
addAtIndex(size, val);
}
public void addAtIndex(int index, int val) {
if (index < 0 || index > size) {
return;
}
ListNode p, q;
//离head近
if (index < size - index + 1) {
q = head;
for (int i = 0; i < index; i++) {
q = q.next;
}
p = q.next;
} else {
p = tail;
//离tail近
for (int i = 0; i < size - index; i++) {
p = p.prev;
}
q = p.prev;
}
size++;
ListNode newNode = new ListNode(val);
newNode.next = p;
q.next = newNode;
newNode.prev = q;
p.prev = newNode;
}
public void deleteAtIndex(int index) {
if (index < 0 || index >= size) {
return;
}
ListNode p, q;
if (index < size - index + 1) {
q = head;
for (int i = 0; i < index; i++) {
q = q.next;
}
p = q.next;
} else {
p = tail;
for (int i = 0; i < size - index; i++) {
p = p.prev;
}
q = p.prev;
}
size--;
q.next = p.next;
p.next.prev = q;
}
}
class ListNode {
int val;
ListNode next;
ListNode prev;
public ListNode(int val) {
this.val = val;
}
}
/**
* Your MyLinkedList object will be instantiated and called as such:
* MyLinkedList obj = new MyLinkedList();
* int param_1 = obj.get(index);
* obj.addAtHead(val);
* obj.addAtTail(val);
* obj.addAtIndex(index,val);
* obj.deleteAtIndex(index);
*/
(简单)206. 反转链表
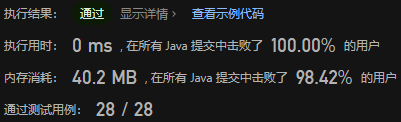
在遍历链表时,将当前节点的next指针改为指向前一个节点。由于节点没有引用其前一个节点,因此必须事先存储其前一个节点。在更改引用之前,还需要存储后一个节点。最后返回新的头引用。
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode() {}
* ListNode(int val) { this.val = val; }
* ListNode(int val, ListNode next) { this.val = val; this.next = next; }
* }
*/
class Solution {
public ListNode reverseList(ListNode head) {
if (head == null || head.next == null) {
return head;
}
ListNode pre = head;
ListNode p = head.next;
pre.next = null;
ListNode q;
while (p != null) {
q = p.next;
p.next = pre;
pre = p;
p = q;
}
return pre;
}
}
复杂度分析:
- 时间复杂度:O(n),其中n是链表的长度。需要遍历链表一次。
- 空间复杂度:O(1)。
官方思路,递归
递归版本复杂一点,其关键在于反向工作。假设链表的其余部分已经被翻转
假设链表为:
n1->n2->n3->…->nk->nk+1->…->nm
若从节点nk+1到nm已经被反转,而现在需要将nk+1指向nk
n1->n2->n3->…->nk->nk+1<-…<-nm
nk.next.next = nk
需要注意的是,n1的下一个节点必须指向空。如果忽略了这一点,链表中可能产生环。
class Solution {
public ListNode reverseList(ListNode head) {
if (head == null || head.next == null) {
return head;
}
ListNode newHead = reverseList(head.next);
head.next.next = head;
head.next = null;
return newHead;
}
}
复杂度分析:
- 时间复杂度:O(n),其中n是链表的长度。需要对链表的每个节点进行反转操作
- 空间复杂度:O(n),其中n是链表的长度。空间复杂度主要取决于递归调用的栈空间,最多为n层。
(中等)24. 两两交换链表中的节点
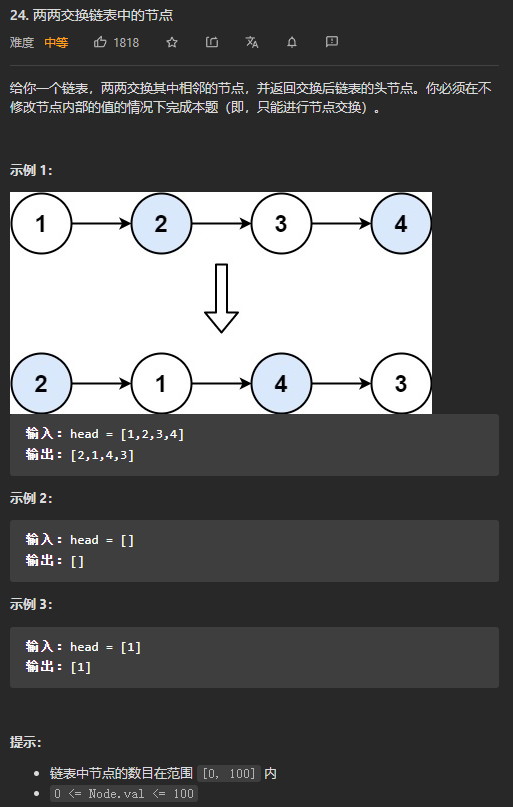
官方思路,方法一:递归
可以通过递归的方式实现两两交换链表中的节点。
递归的终止条件是链表中没有节点,或者链表中只有一个节点,此时无法进行交换。
如果链表中至少有两个节点,则在两两交换链表中的节点之后,原始链表的头节点编程新的链表的第二个节点,原始链表的第二个节点变成新的链表的头节点。
链表中的其余节点的两两交换可以递归地实现。在对链表中地其余节点递归地两两交换之后,更新节点之间的指针关系,即可完成整个链表的两两交换。
用head表示原始链表的头节点,新的链表的第二个节点,用newHead表示新的链表的头节点,原始链表的第二个节点,则原始链表中的其余节点的头节点是newHead.next。令head.next=swapPairs(newHead.next),表示将其余节点进行两两交换,交换后新的头节点为head的下一个节点。然后令newHead.next = head,即完成了所有节点的交换。最后返回新的链表的头节点newHead。
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode() {}
* ListNode(int val) { this.val = val; }
* ListNode(int val, ListNode next) { this.val = val; this.next = next; }
* }
*/
class Solution {
public ListNode swapPairs(ListNode head) {
if (head == null || head.next == null) {
return head;
}
ListNode newHead = head.next;
head.next = swapPairs(newHead.next);
newHead.next = head;
return newHead;
}
}
复杂度分析:
- 时间复杂度:O(n),其中n是链表的节点数量。需要对每个节点进行更新指针的操作。
- 空间复杂度:O(n),其中n是链表的节点数量。空间复杂度主要取决于递归调用的栈空间。
官方思路,方法二:迭代
也可以通过迭代的方式实现两两交换链表中的节点。
创建哑节点dummyHead,令dummyHead.next = head。令temp表示当前到达的节点,初始时temp = dummyHead。每次需要交换temp后面的两个节点。
如果temp的后面没有节点或者只有一个节点,则没有更多的节点需要交换,因此结束交换。否则,获得temp后面的两个节点node1和node2,通过更新节点的指针关系实现两两交换节点。
具体而言,交换前的节点关系是temp->node1->node2
交换后的节点关系要变成temp->node2->node1
temp.next = node2
node1.next = node2.next
node2.nexr = node1
完成上面的3步操作后,再令temp=node1,对链表的其余节点进行两两交换,直到全部节点都被两两交换。
两两节点交换之后,新的链表的头节点是dummyHead.next。
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode() {}
* ListNode(int val) { this.val = val; }
* ListNode(int val, ListNode next) { this.val = val; this.next = next; }
* }
*/
class Solution {
public ListNode swapPairs(ListNode head) {
if (head == null || head.next == null) {
return head;
}
ListNode preHead = new ListNode(-1);
preHead.next = head;
ListNode temp = preHead;
while (temp.next!=null && temp.next.next != null) {
ListNode node1 = temp.next;
ListNode node2 = temp.next.next;
temp.next = node2;
node1.next = node2.next;
node2.next = node1;
temp = node1;
}
return preHead.next;
}
}
复杂度分析:
- 时间复杂度:O(n),其中n表示链表的节点数量。需要对每个节点进行更新指针的操作,
- 空间复杂度:O(1)
(中等)19. 删除链表的倒数第 N 个结点
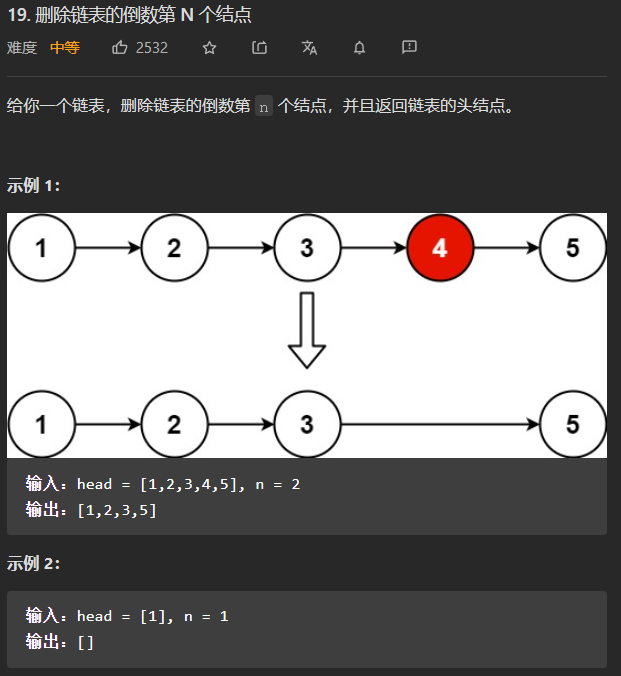
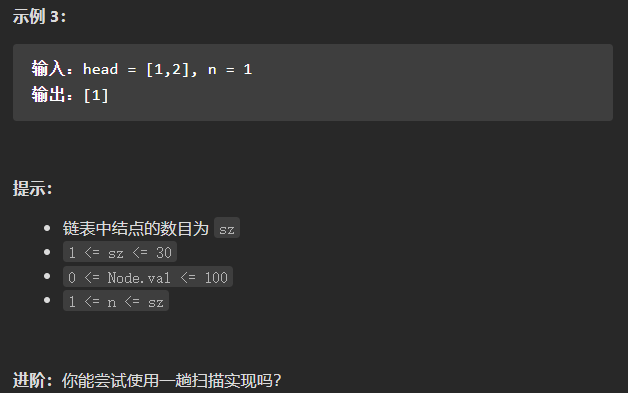
我的思路,首先顺序遍历一遍链表,统计该链表有多少个节点,然后题目中给出的是倒数第N个结点,算出要删除的节点是正数的第多少个,删除它
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode() {}
* ListNode(int val) { this.val = val; }
* ListNode(int val, ListNode next) { this.val = val; this.next = next; }
* }
*/
class Solution {
public ListNode removeNthFromEnd(ListNode head, int n) {
int count = 0;
ListNode p = head;
while (p != null) {
count++;
p = p.next;
}
n = count - n + 1;
ListNode pre = new ListNode(-1);
pre.next = head;
ListNode q = pre;
p = head;
for (int i = 1; i < n; i++) {
q = q.next;
p = p.next;
}
q.next = p.next;
return pre.next;
}
}
复杂度分析:
- 时间复杂度:O(L),其中,L是链表的长度
- 空间复杂度:O(1)
官方其他思路,栈
在遍历链表的同时将所有节点一次入栈。根据栈【先进后出】的原则,弹出栈的第n个节点就是需要删除的节点,并且,目前栈顶的节点就是待删除节点的前驱节点。
import java.util.Stack;
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode() {}
* ListNode(int val) { this.val = val; }
* ListNode(int val, ListNode next) { this.val = val; this.next = next; }
* }
*/
class Solution {
public ListNode removeNthFromEnd(ListNode head, int n) {
ListNode preHead = new ListNode(-1, head);
Stack<ListNode> stack = new Stack<>();
ListNode p = preHead;
while (p != null) {
stack.push(p);
p = p.next;
}
for (int i = 0; i < n; i++) {
stack.pop();
}
ListNode prev = stack.peek();
prev.next = prev.next.next;
return preHead.next;
}
}
复杂度分析:
- 时间复杂度:O(L),其中L是链表的长度
- 空间复杂度:O(L),其中L是链表的长度。主要为栈的开销
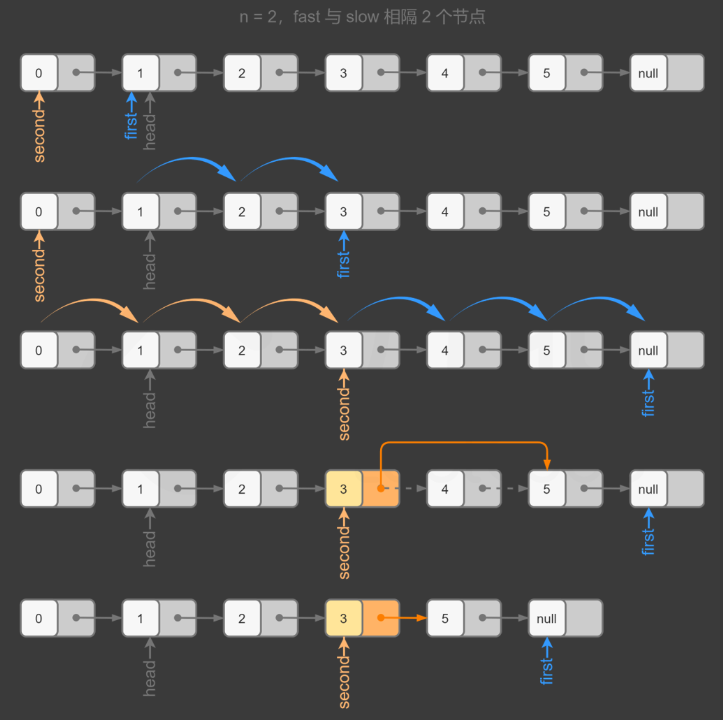
官方其他思路,双指针
由于需要删除倒数第n个节点,因此可以使用两个指针first和second同时对链表进行遍历,其中first是快指针,second是慢指针
first比second超前n个节点,也就是first和second中间间隔了n个节点,那么当first指向空时,second正好指向的是要删除节点的前一个节点
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode() {}
* ListNode(int val) { this.val = val; }
* ListNode(int val, ListNode next) { this.val = val; this.next = next; }
* }
*/
class Solution {
public ListNode removeNthFromEnd(ListNode head, int n) {
ListNode preHead = new ListNode(-1, head);
ListNode first = preHead;
ListNode second = preHead;
for (int i = 0; i <= n; i++) {
first = first.next;
}
while (first != null) {
second = second.next;
first = first.next;
}
second.next = second.next.next;
return preHead.next;
}
}
复杂度分析:
- 时间复杂度:O(L),其中L是链表的长度
- 空间复杂度:O(1)
(简单)面试题 02.07. 链表相交
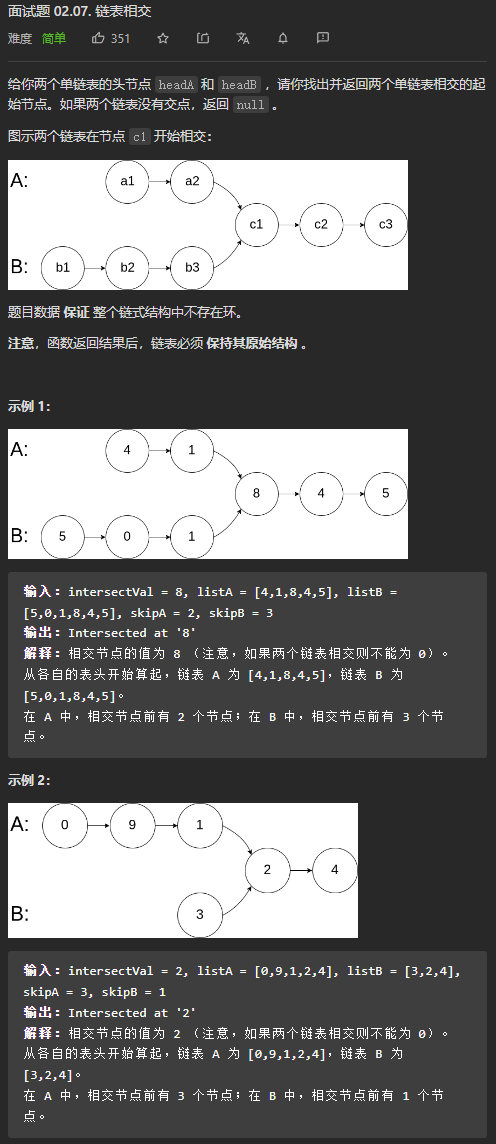
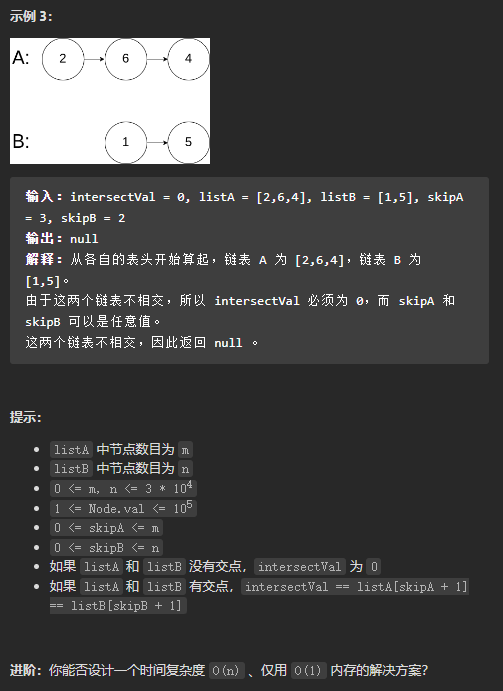
我的思路,将节点存到HashSet中,当要加入某节点时,如果set中已经存在该节点,那么该节点就是两个链表相交的节点
import java.util.HashSet;
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode(int x) {
* val = x;
* next = null;
* }
* }
*/
public class Solution {
public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
ListNode p = headA;
ListNode q = headB;
HashSet<ListNode> set = new HashSet<>();
ListNode ans = null;
while (p != null || q != null) {
if (p != null) {
if (set.add(p)) {
p = p.next;
} else {
ans = p;
break;
}
}
if (q != null) {
if (set.add(q)) {
q = q.next;
} else {
ans = q;
break;
}
}
}
return ans;
}
}
官方思路,方法一:哈希集合
判断两个集合是否相交,可以使用哈希集合存储链表节点。
首先判断链表headA,并将链表headA中的每个节点加入哈希集合中。然后遍历链表headB,对于遍历到的每个节点,判断该节点是否在哈希集合中:
- 如果当前节点不在哈希集合中,则继续遍历下一个节点
- 如果当前节点在哈希集合中,则后面的节点都在哈希集合中,即从当前节点开始的所有节点都在两个链表的相交部分,因此在链表中headB中遍历到的第一个在哈希集合中的节点就是两个链表相交的节点,返回该节点
如果链表headB中的所有节点都不在哈希集合中,则两个链表不相交,返回null。
import java.util.HashSet;
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode(int x) {
* val = x;
* next = null;
* }
* }
*/
public class Solution {
public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
HashSet<ListNode> set = new HashSet<>();
ListNode temp = headA;
while (temp != null) {
set.add(temp);
temp = temp.next;
}
temp = headB;
while (temp != null) {
if (set.contains(temp)) {
return temp;
}
temp = temp.next;
}
return null;
}
}
复杂度分析:
- 时间复杂度:O(m+n),其中m+n分别表示headA和headB的链表长度之和。需要遍历两个链表各一次
- 空间复杂度:O(m),其中m是链表headA的长度。需要使用哈希集合存储headA中的全部节点。
官方思路,方法二:双指针
使用双指针方法,可以将空间复杂度降至O(1)
只有当链表headA和headB不为空时,两个链表才可能相交。所以,首先判断两个链表是否为空
当链表headA和headB都不为空时,创建两个指针pA和pB,初始时分别指向两个链表的头节点headA和headB,然后将两个指针依次遍历两个链表的每个节点。具体做法如下:
- 每步操作需要同时更新pA和pB
- 如果指针A不为空,则将指针pA移动到下一个节点;如果指针pB不为空,则将指针pB移动到下一个节点
- 如果指针pA为空,则将指针pA移动到链表headB的头节点;如果指针pB为空,则将指针pB移动到headA的头节点
- 当指针pA和pB指向同一个节点或者都为空时,返回他们指向的节点或者null
官方给出的证明:

import java.util.HashSet;
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode(int x) {
* val = x;
* next = null;
* }
* }
*/
public class Solution {
public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
if (headA == null || headB == null) {
return null;
}
ListNode pA = headA, pB = headB;
while (pA != pB) {
pA = (pA == null ? headB : pA.next);
pB = (pB == null ? headA : pB.next);
}
return pA;
}
}
(*中等)142. 环形链表 II
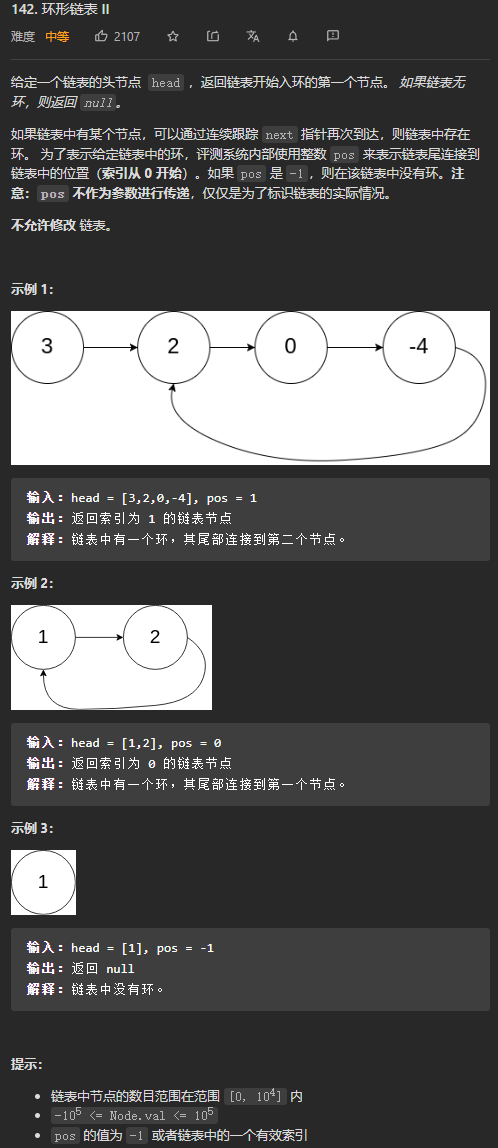
我的思路:用HashSet存储节点,当添加某一结点时,如果该节点已经存在于set中,那么就说明该节点是进入环形链表的第一个节点
import java.util.HashSet;
/**
* Definition for singly-linked list.
* class ListNode {
* int val;
* ListNode next;
* ListNode(int x) {
* val = x;
* next = null;
* }
* }
*/
public class Solution {
public ListNode detectCycle(ListNode head) {
if (head == null) {
return head;
}
ListNode p = head;
HashSet<ListNode> set = new HashSet<>();
ListNode ans = null;
while (p != null) {
if (set.add(p)) {
p = p.next;
} else {
ans = p;
break;
}
}
return ans;
}
}
复杂度分析:
- 时间复杂度:O(N),其中N为链表中节点的数目。恰好需要访问链表中的每一个节点。
- 空间复杂度:O(N),其中N为链表中的节点数目。我们将链表中的每个节点都保存在哈希表当中
官方其他思路,快慢指针
使用两个指针,fast和slow。它们起始都位于链表的头部。随后,slow指针每次向后移动一个位置,而fast指针每次向后移动两个位置。如果链表中存在环,则fast指针最终再次与slow指针在环中相遇。
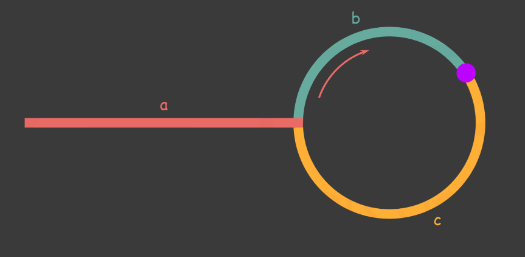
设链表中环外的部分的长度为a。slow指针进入环后,又走了b的距离与fast相遇。此时fast指针已经走完了环的n圈。因此,它走过的距离是a+n(b+c)+b=a+(n+1)b+nc
根据题意,任意时刻,fast走过的距离都是slow指针的两倍。因此,有:
a+(n+1)b+nc=2(a+b) => a=c+(n-1)(b+c)
有了上面推导出来的式子,就会发现,从相遇点到入环点的距离加上n-1圈的环长,恰好等于从链表头部到入环点的距离。
因此,当发现slow与fast相遇时,再额外使用一个指针,它指向链表头部;随后,他和slow每次向后移动一个位置。最终,它们会在入环点相遇
import java.util.HashSet;
/**
* Definition for singly-linked list.
* class ListNode {
* int val;
* ListNode next;
* ListNode(int x) {
* val = x;
* next = null;
* }
* }
*/
public class Solution {
public ListNode detectCycle(ListNode head) {
if (head == null) {
return null;
}
ListNode slow = head;
ListNode fast = head;
while (fast != null) {
slow = slow.next;
if (fast.next != null) {
fast = fast.next.next;
} else {
return null;
}
if (fast == slow) {
ListNode p = head;
while (p != slow) {
p = p.next;
slow = slow.next;
}
return p;
}
}
return null;
}
}
复杂度分析:
- 时间复杂度:O(N),其中N为链表中节点的数目。在最初判断快慢指针是否相遇时,slow指针走过的距离不会超过链表的总长度;随后寻找入环点时,走过的距离也不会超过链表的总长度。因此,总的执行时间为O(N)+O(N)=O(N)
- 空间复杂度:O(1),只使用了fast,slow,p指针