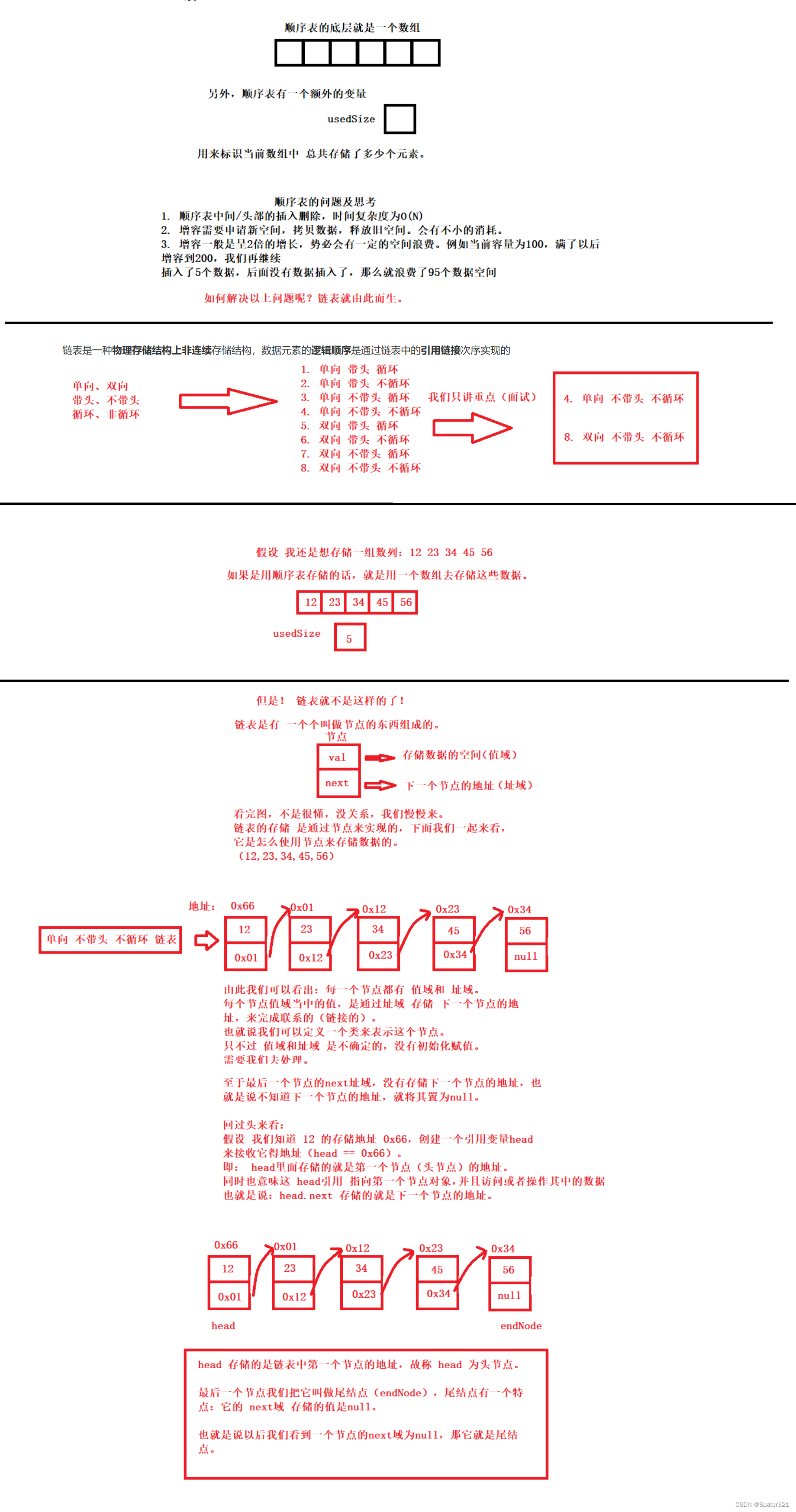
顺序表的问题及思考:
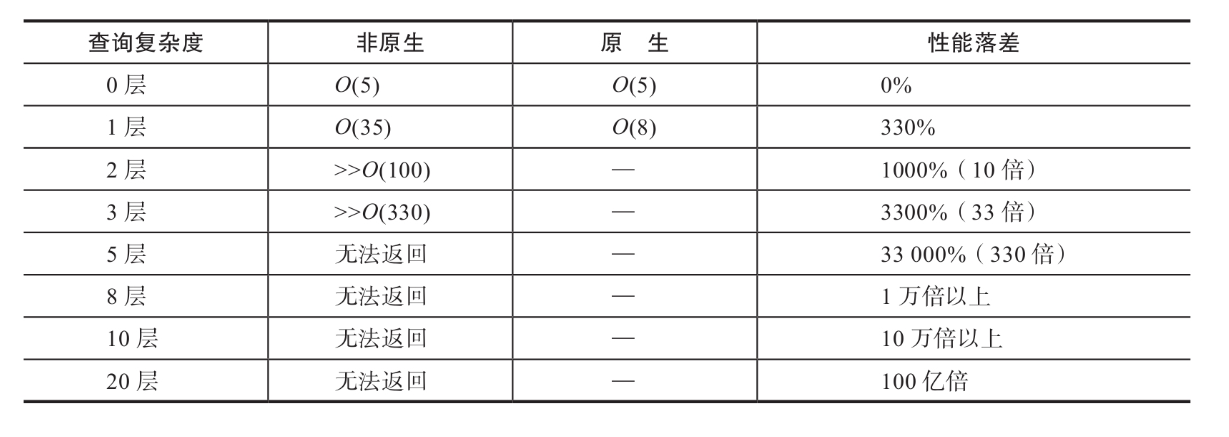
- 顺序表中间/头部的插入删除,时间复杂度为O(N)
- 增容需要申请新空间,拷贝数据,释放旧空间。会有不小的消耗。
- 增容一般是呈2倍的增长,势必会有一定的空间浪费。例如当前容量为100,满了以后增容到200,我们再继续插入了5个数据,后面没有数据插入了,那么就浪费了95个数据空间
思考: 如何解决以上问题呢?下面给出了链表的结构来看看
一、链表
1.1、链表的概念及结构
链表是一种物理存储结构上非连续存储结构,数据元素的逻辑顺序是通过链表中的引用链接次序实现的
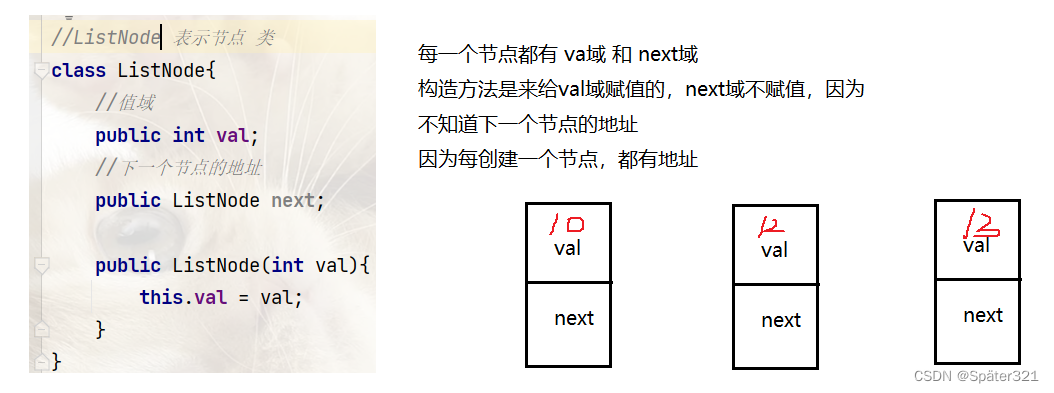
1.1.1、创建一个类表示节点 - ListNode
//NodeList 表示节点 类
class ListNode{
//值域
public int val;
//下一个节点的地址
public ListNode next;
public ListNode(int val){
this.val = val;
}
}
1.1.2、创建一个类来表示链表 - MyLinkedList
//ListNode 表示节点 类
class ListNode{
//值域
public int val;
//下一个节点的地址
public ListNode next;
public ListNode(int val){
this.val = val;
}
}
public class MyLinkedList {
public static void main(String[] args) {
//当new 一个节点的时候就是创建一个节点,值为 1
ListNode nodeList = new ListNode(1);
}
}
new 一个节点

如和创建多个节点,让这些节点串起来
首先要有一个头结点
单向,带头,不循环的单链表
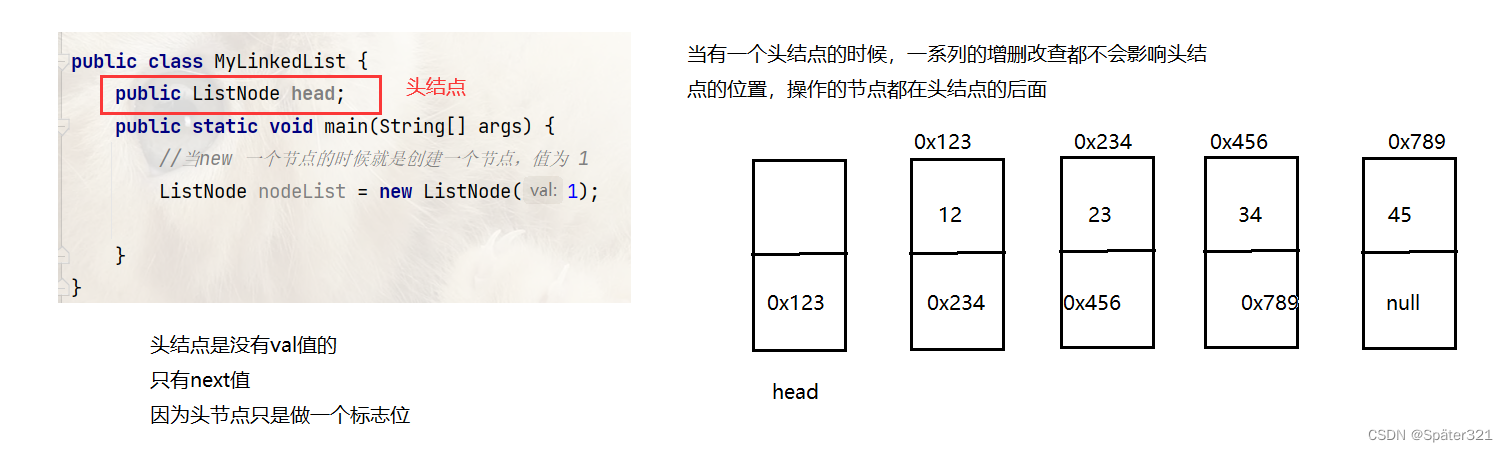
理解链表中: 带头、不带头、单向、双向、循环、不循环的意思
带头 和 不带头

循环 和 不循环
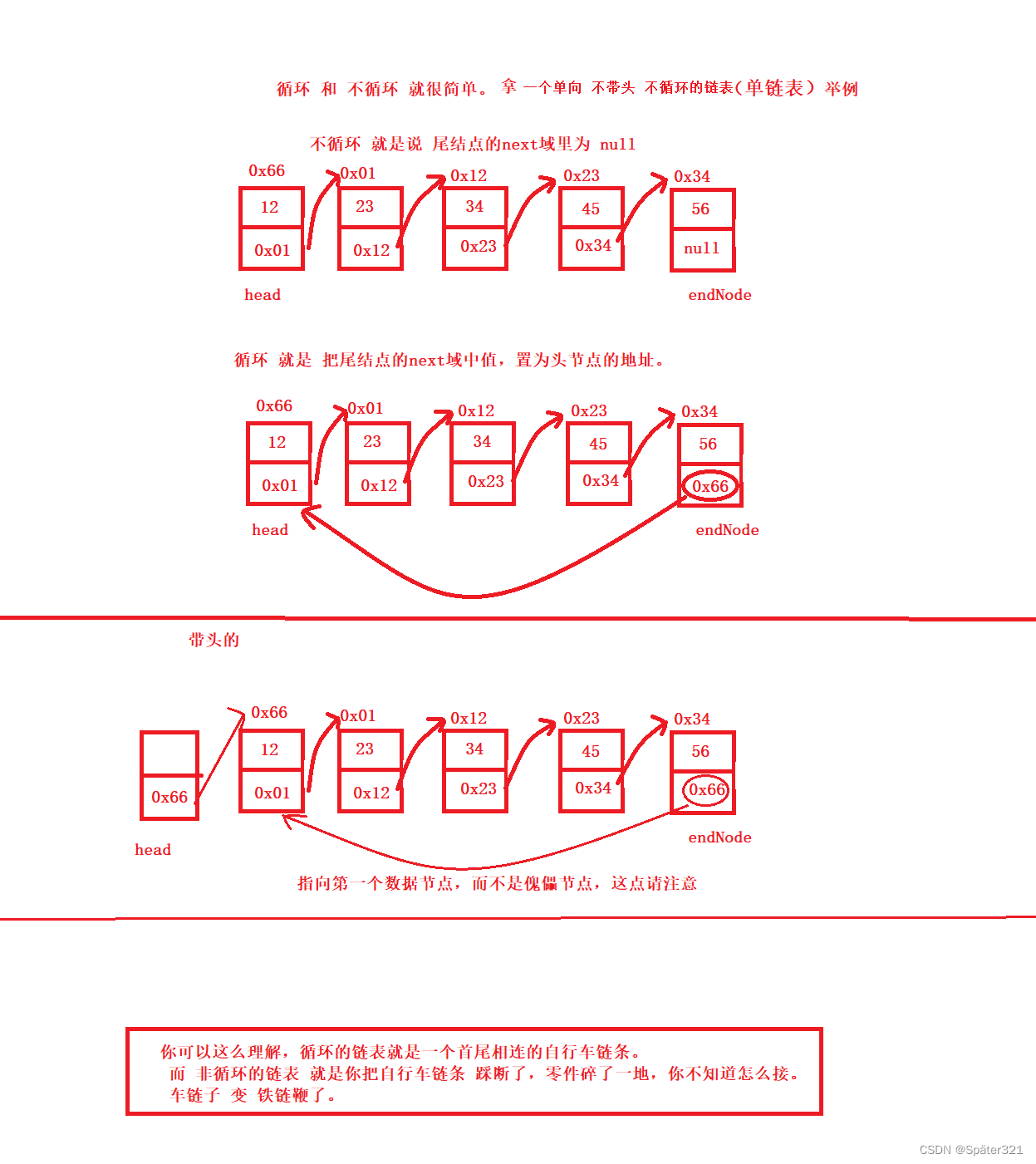
单向 和 双向
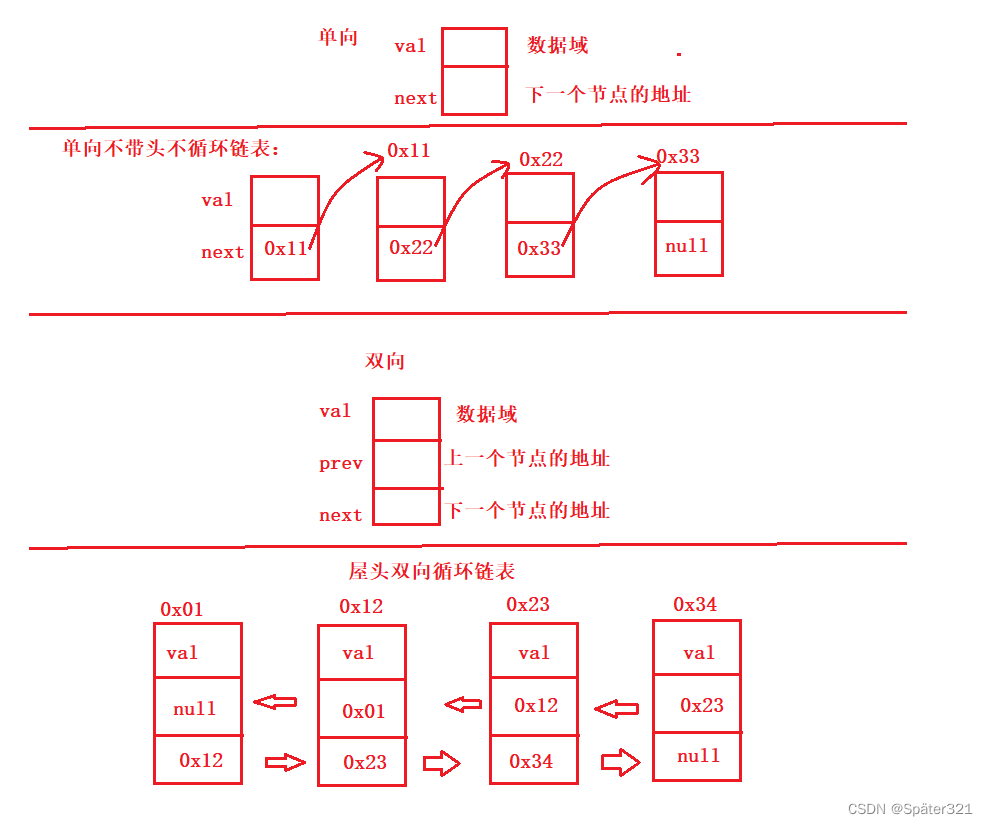
1.1.3、模拟实现 单向 不带头 非循环的链表
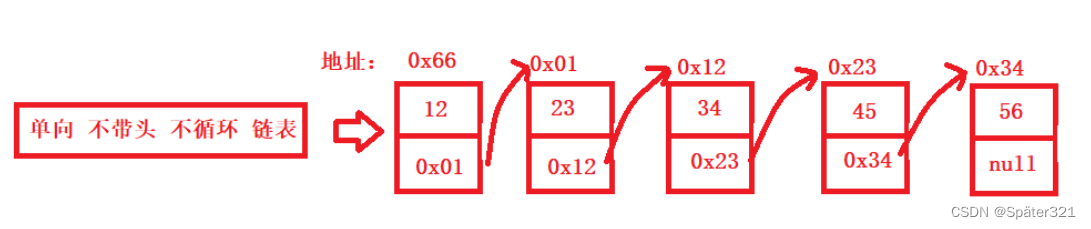
用过列举的方式,创建几个节点,然后将他们连接起来
//ListNode 表示节点 类
class ListNode{
//值域
public int val;
//下一个节点的地址
public ListNode next;
public ListNode(int val){
this.val = val;
}
}
public class MyLinkedList {
public ListNode head;
//创建5个节点的链表
public void creatList(){
//当new 一个节点的时候就是创建一个节点,值为 1
ListNode ListNode1 = new ListNode(10);
ListNode ListNode2 = new ListNode(20);
ListNode ListNode3 = new ListNode(30);
ListNode ListNode4 = new ListNode(40);
ListNode ListNode5 = new ListNode(50);
ListNode1.next = ListNode2;
ListNode2.next = ListNode3;
ListNode3.next = ListNode4;
ListNode4.next = ListNode5;
this.head = ListNode1;
}
}
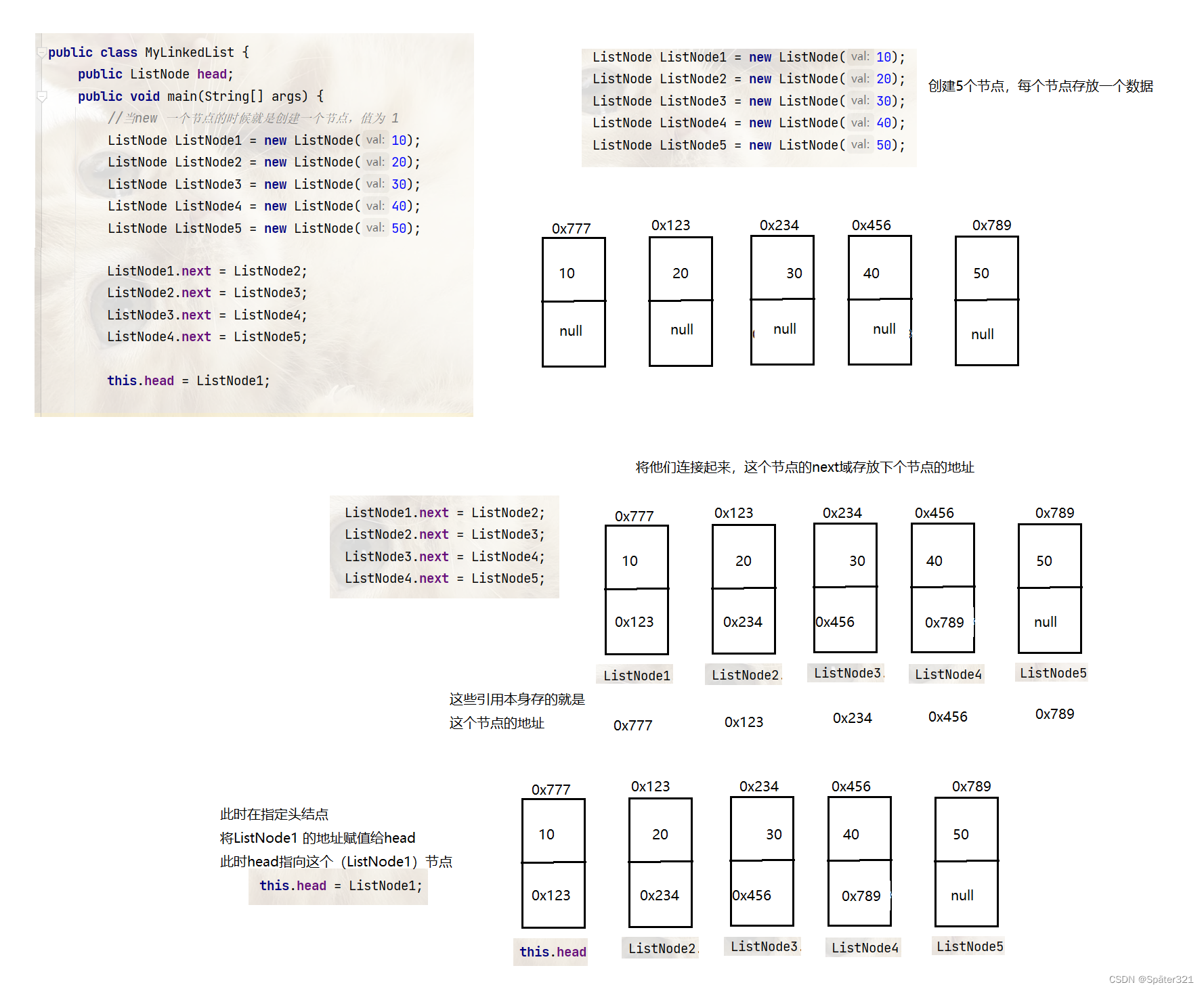
此时就有5个节点了
1.1.4、遍历链表数据
首先,我要区分清楚,链表 不是顺序表,不是一块连续的空间。 链表的每个元素 是由地址来连接起来的。
也就是说 我们不能使用普通思维模式 去思考 遍历链表的数据域的值
既然 链表是靠地址联系起来的,也就是说 靠 next域中 存储的地址来联系个节点的数据,
这就是我们突破点。
利用 head 遍历每个每个节点的数据 写法 head = head.next,你可以参考上面的图,来细品。
这样我们就跳转到下一个节点,算了我还是画个图,请看下图
//打印链表的数据
public void disPlay(){
ListNode cur = this.head;
while(cur != null){
System.out.print(cur.val + " " );
cur = cur.next;
}
System.out.println();
}

测试一下:
public class TestDome {
public static void main(String[] args) {
MyLinkedList myLinkedList = new MyLinkedList();
myLinkedList.creatList();
myLinkedList.disPlay();
}
}
1.2、链表里面的操作
1.2.1、得到单链表的长度
//得到单链表的长度
public int size(){
int usedSize = 0;
ListNode cur = this.head;
while(cur != null){
cur = cur.next;
usedSize++;
}
return usedSize;
};
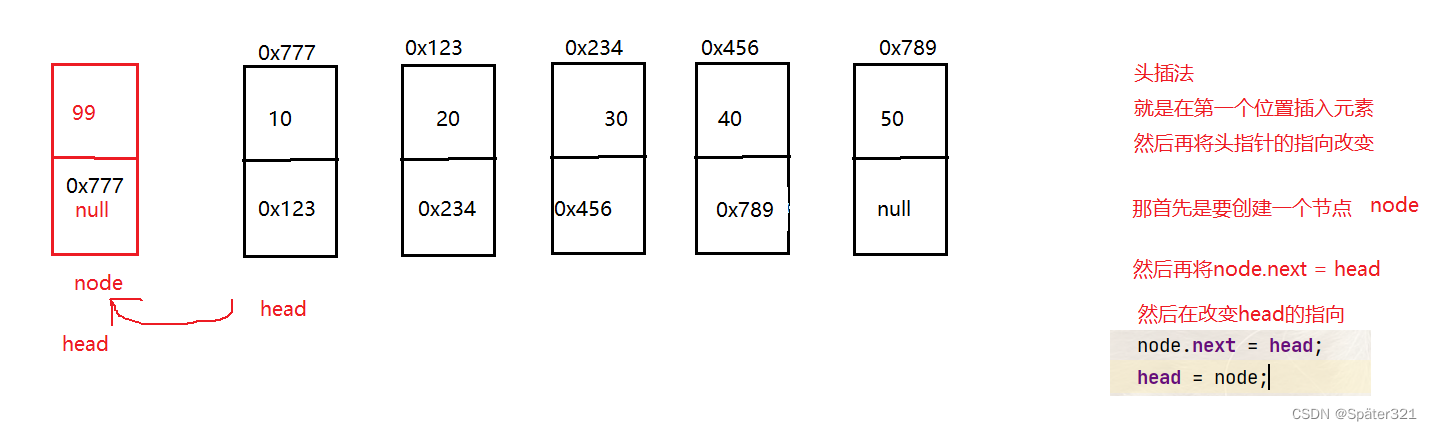
1.2.2、头插法
//头插法
public void addFirst(int data){
ListNode node = new ListNode(data);
node.next = head;
head = node;
};
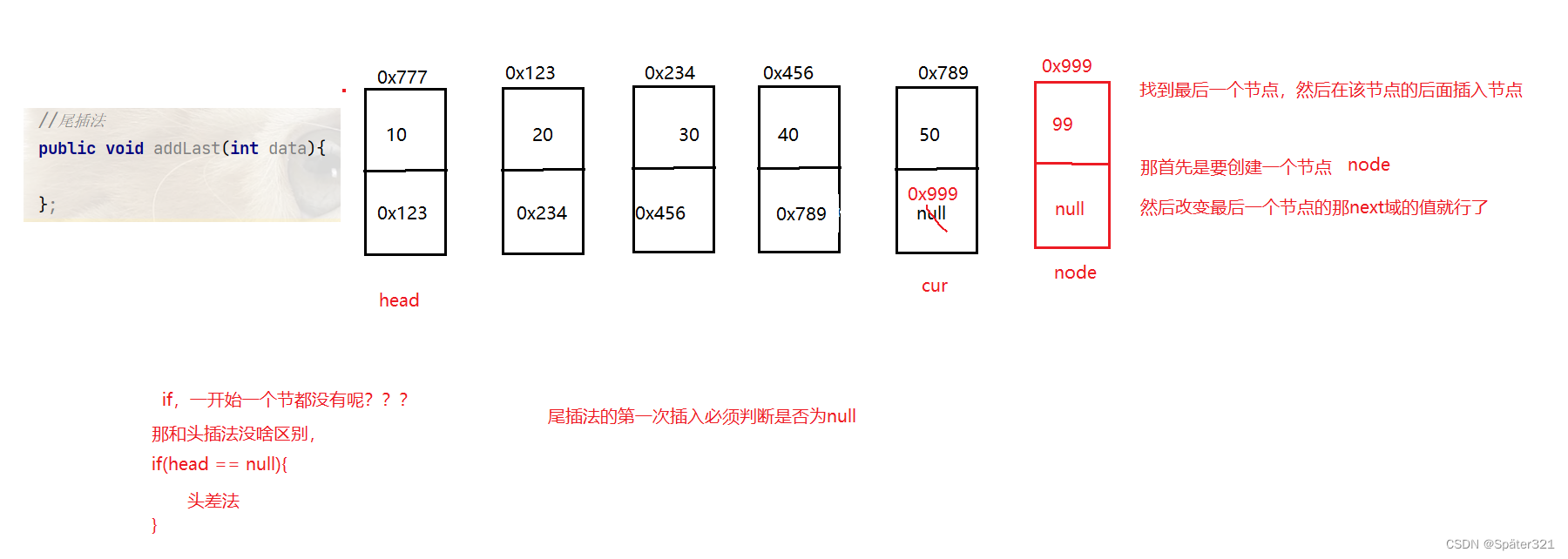
1.2.3、尾插法
//尾插法
public void addLast(int data){
ListNode node = new ListNode(data);
ListNode cur = this.head;
//判断链表是否为空
if(this.head == null){
this.head = node;
} else{
while(cur.next != null){
cur = cur.next;
}
cur.next = node;
}
};
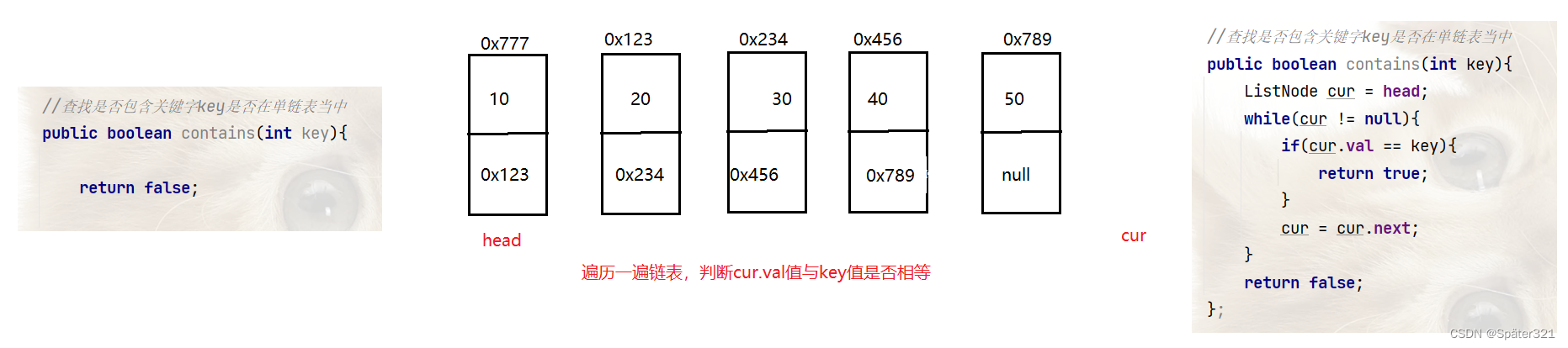
1.2.4、查找是否包含关键字key是否在单链表当中
//查找是否包含关键字key是否在单链表当中
//查找是否包含关键字key是否在单链表当中
public boolean contains(int key){
ListNode cur = head;
while(cur != null){
if(cur.val == key){
return true;
}
cur = cur.next;
}
return false;
};
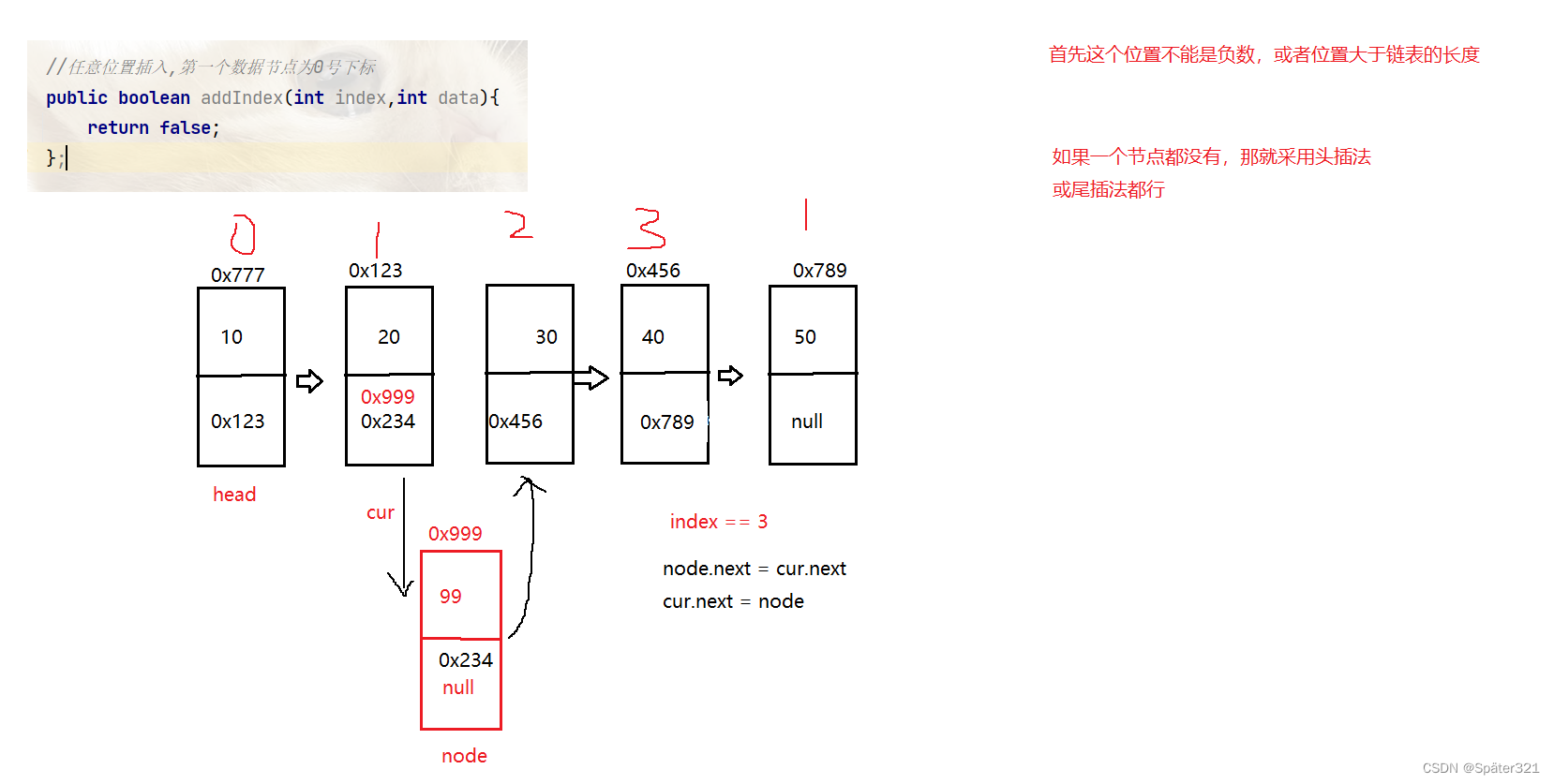
1.2.5、任意位置插入,第一个数据节点为0号下标
/任意位置插入,第一个数据节点为0号下标
public void addIndex(int index,int data){
ListNode node = new ListNode(data);
if(index < 0 || index > size()){
System.out.println("index 位置不合法!");
return;
}
if(index == 0){
addFirst(data);
return;
}
if(index == size()){
addLast(data);
return;
}
//中间位置
ListNode cur = this.head;
while(index - 1 != 0){
cur = cur.next;
index--;
}
node.next = cur.next;
cur.next = node;
};
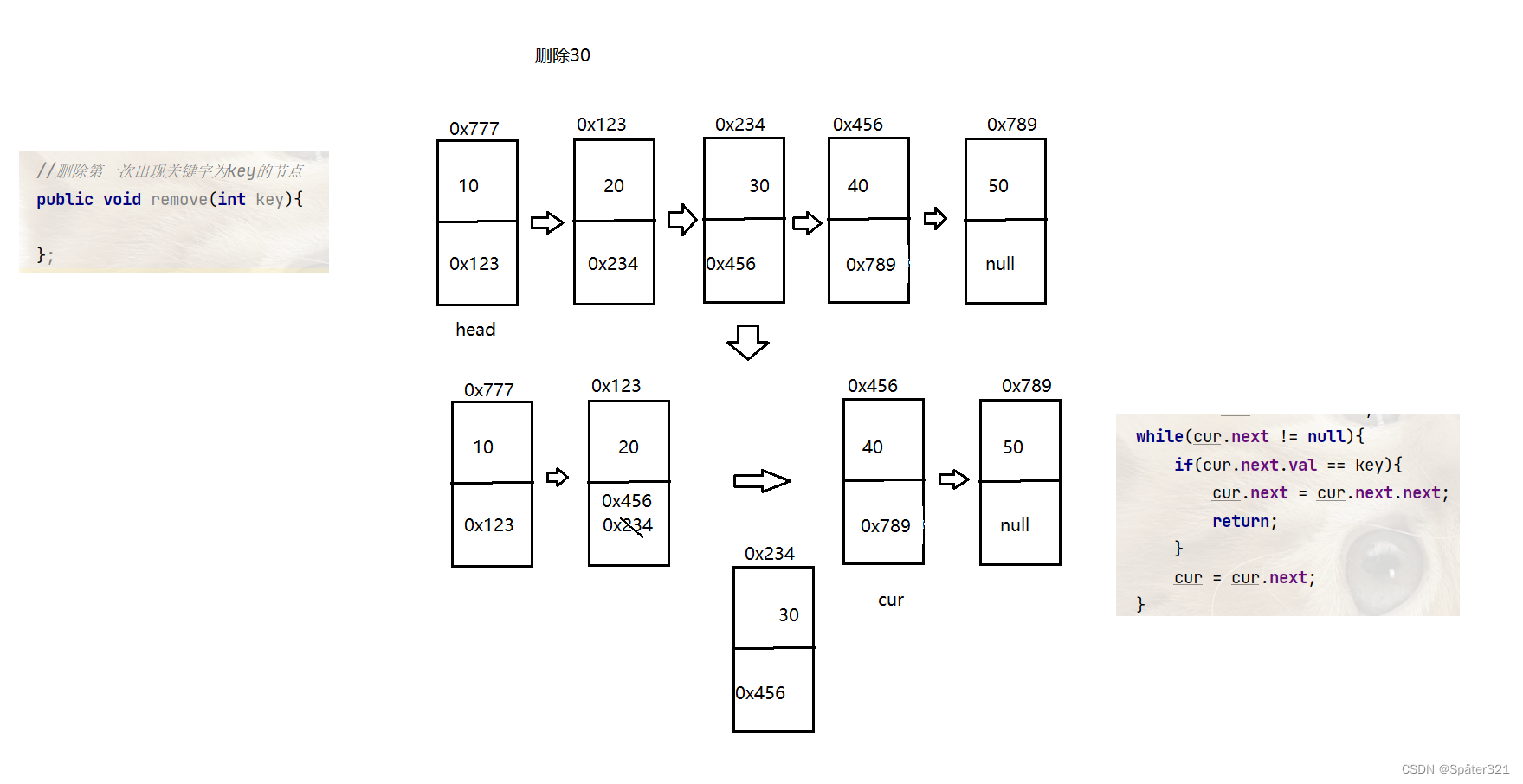
1.2.6、删除第一次出现关键字为key的节点
//删除第一次出现关键字为key的节点
public void remove(int key){
//当链表为空的时候
if(size() == 0){
System.out.println("删除失败,链表为空!");
return;
}
//当删除的是头节点的时候
if(this.head.val == key){
this.head = this.head.next;
return;
}
ListNode cur = this.head;
while(cur.next != null){
if(cur.next.val == key){
cur.next = cur.next.next;
return;
}
cur = cur.next;
}
return;
};
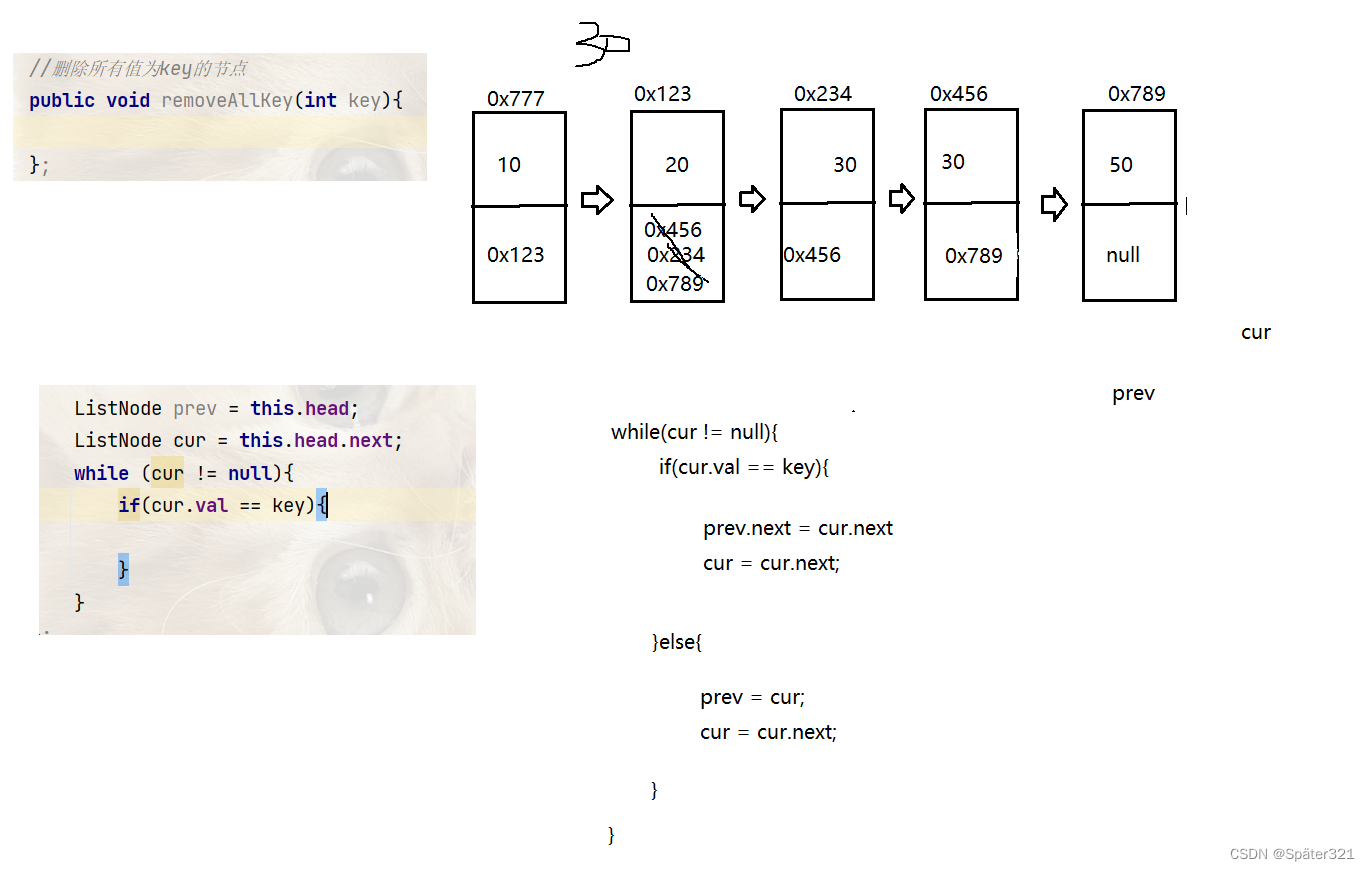
1.2.7、删除所有值为key的节点
//删除所有值为key的节点
public void removeAllKey(int key){
if(this.head == null){
System.out.println("链表为空!");
return;
}
//cur.val 就是删除的值
ListNode prev = this.head;
ListNode cur = this.head.next;
while (cur != null){
if(cur.val == key){
prev.next = cur.next;
cur = cur.next;
}else{
prev = cur;
cur = cur.next;
}
}
//删除头结点
if(head.val == key){
this.head = head.next;
}
};
1.2.8、清除单链表
清除链表里面的数据的时候,最好是一个节点一个节点的释放(置为null)
//清除单链表
public void clear(){
//粗暴的做法
//this.head = null;
while (this.head != null){
ListNode curNext = this.head;
this.head = null;
head = curNext;
}
};