正态分布

正态分布，最早由棣莫弗在二项分布的渐近公式中得到，而真正奠定其地位的，应是高斯对测量误差的研究，故而又称Gauss分布。。测量是人类定量认识自然界的基础，测量误差的普遍性，使得正态分布拥有广泛的应用场景，或许正因如此，正太分布在分布族谱图中居于核心的位置。

正态分布$N(\mu ,\sigma )$受到期望$\mu$和方差KaTeX parse error: Undefined control sequence: \simga at position 1: \̲s̲i̲m̲g̲a̲^2的调控，其概率密度函数为

$$\frac{1}{\sqrt{2\pi {\sigma }^2}}\exp [-\frac{(x-\mu {)}^2}{2{\sigma }^2}]$$

当$\mu =0$而$\sigma =1$时，为标准正态分布$N(0,1)$，对应概率分布函数为$\Phi (x)=\frac{1}{\sqrt{2\pi }}\exp [-\frac{x^2}{2}]$，形状如下，

在scipy.stats中，分别封装了正态分布类norm和标准正态分布类halfnorm。

对数正态分布的推导

假设$Z$满足标准正态分布$Z\sim N(0,1)$，则随机变量$X=a^Z$符合对数正态分布。

根据定义，可以很方便地推导出对数正态分布的概率密度函数，由于$z={\log }_{a}x$，则

$$\begin{array}{rl}{f}_X(x)& =\frac{\text{d}P(X⩽x)}{\text{d}x}=\frac{\text{d}P({\log }_{a}X⩽{\log }_{a}x)}{\text{d}x}\\ & =\frac{\text{d}\Phi ({\log }_{a}x)}{\text{d}x}=\frac{1}{x\ln a}\frac{\text{d}\Phi (z)}{\text{d}z}\end{array}$$

记$s=\ln a$，可得到

$$f(x,s)=\frac{1}{sx\sqrt{2\pi }}\exp (-\frac{{\ln }^{2}x}{2s^2})$$

测试

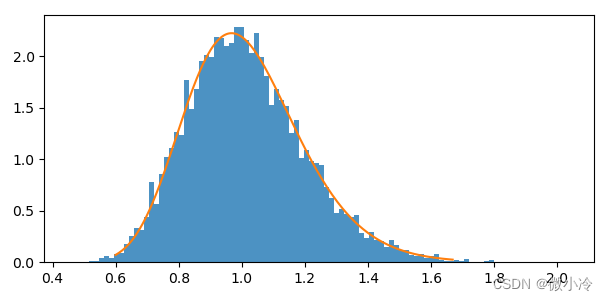
在scipy.stat中，lognorm为对数正态分布类，下面对正态分布和对数正态分布做一个简单的映射。

import numpy as np
import scipy.stats as ss
import matplotlib.pyplot as plt
r = ss.norm.rvs(size=10000)
re = 1.2 ** r               # 这些数值将符合a=1.2的对数正态分布

plt.hist(re, density=True, bins=100, alpha=0.8)

rv = ss.lognorm(np.log(1.2))
st, ed = rv.interval(0.995)
xs = np.linspace(st, ed, 200)
plt.plot(xs, rv.pdf(xs))
plt.show()

效果如下