Sparse编码和字典学习
- 1. 稀疏表示与字典学习简介
- 1.1 Motivation
- 1.2 字典学习的流程
- 1.3 字典学习的数学模型
- 2 python实现
- 2.1字典学习
- 2.1 稀疏性统计和误差计算
- 参考资料和文献
1. 稀疏表示与字典学习简介
1.1 Motivation
字典学习的思想应该源来实际生活中的字典的概念。字典是前辈们学习总结的精华,当我们需要学习新的知识的时候,不必与先辈们一样去学习先辈们所有学习过的知识,我们可以参考先辈们给我们总结的字典,通过查阅这些字典,我们可以大致学会到这些知识。
稀疏表示的一个通俗解释:
设观察到的信号为
y
\bold y
y, 字典为
A
\bold A
A,查找一个稀疏的
x
\bold x
x,满足
y
=
A
x
\bold y=\bold A \bold x
y=Ax
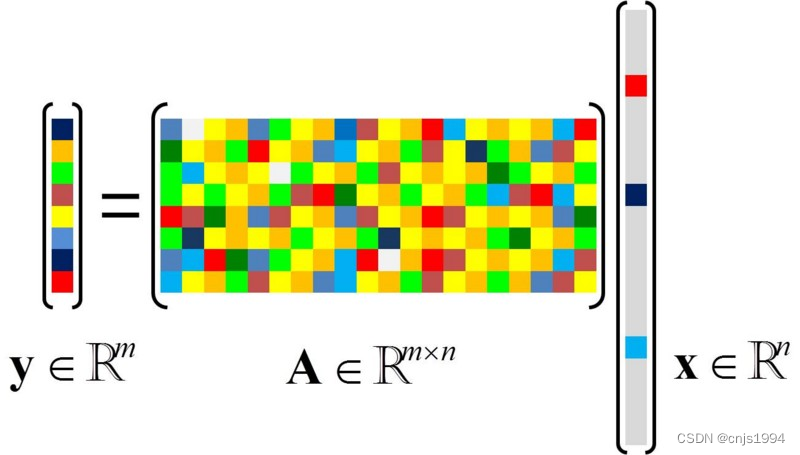
由于
x
\bold x
x的稀疏性质,因而,等式可以改写为如下形式:
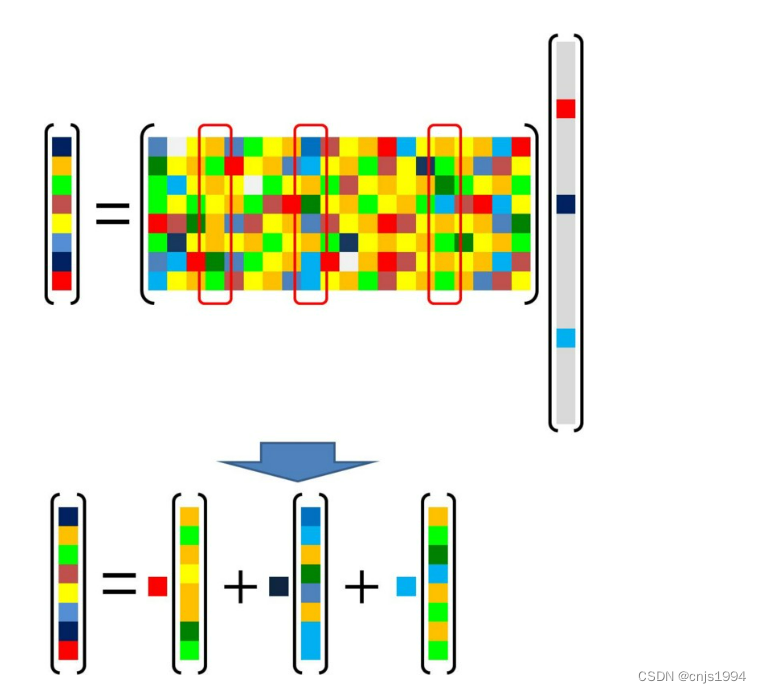
即:原始信号可被近似表示为稀疏矩阵
x
\bold x
x中较少的几个量的叠加。
那么,如何找到这个稀疏矩阵
x
\bold x
x呢?
这个问题可以表示为如下的数学形式:
x
∗
=
a
r
g
min
x
∥
x
∥
0
s
u
b
j
e
c
t
t
o
A
x
=
y
\boldsymbol{x}^*=\underset{\boldsymbol{x}}{arg\min}\left\| \left. \boldsymbol{x} \right\| _0\,\,subject\,\,to\,\,\boldsymbol{Ax}=\boldsymbol{y} \right.
x∗=xargmin∥x∥0subjecttoAx=y
PS:范数是一种强化的距离概念,它在定义上比距离多了一条数乘的运算法则。
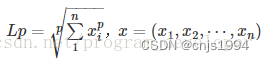
零范数即p取0。
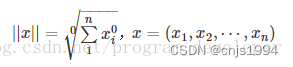
当P=0时,也就是L0范数,L0范数并不是一个真正的范数,它主要被用来度量向量中非零元素的个数。
下面,继续回到正题,但是,直接求解这个问题(NP hard)较为困难,
这个问题可被放松为以下条件形式:
x
∗
=
a
r
g
min
∥
y
−
A
x
∥
2
2
s
u
b
j
e
c
t
t
o
∥
x
∥
0
⩽
ϵ
\boldsymbol{x}^*=arg\min \left\| \left. \boldsymbol{y}-\boldsymbol{Ax} \right\| _{2}^{2}\,\, subject\,\,to\,\,\left\| \left. \boldsymbol{x} \right\| _0\leqslant \epsilon \right. \right.
x∗=argmin∥∥∥y−Ax∥22subjectto∥x∥0⩽ϵ
但上式只考虑了观测信号
A
x
\bold Ax
Ax和真实信号
y
\bold y
y之间的平方和误差,优化过程,只是添加了一个硬性的L0范数的约束条件,因而,迭代过程缺乏对稀疏性的优化,进而修改为如下形式:
x
∗
=
a
r
g
min
1
2
∥
y
−
A
x
∥
2
2
+
λ
∥
x
∥
1
\boldsymbol{x}^*=arg\min \frac{1}{2}\left\| \left. \boldsymbol{y}-\boldsymbol{Ax} \right\| _{2}^{2}+\lambda \left\| \left. \boldsymbol{x} \right\| _1 \right. \right.
x∗=argmin21∥∥∥y−Ax∥22+λ∥x∥1
探索了下,获取稀疏解的原理和过程,实际上LASSO也并不是一种封闭形式的优化过程( a closed form for the lasso solution),为了获得稀疏解
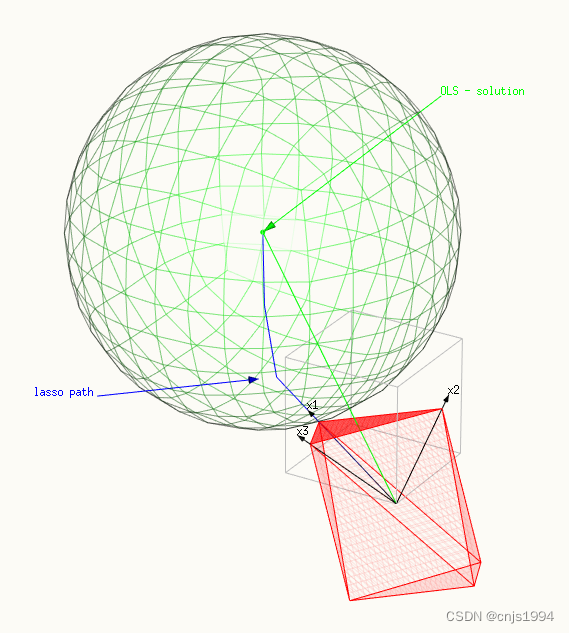
1.2 字典学习的流程
因而,基于上述的一个思想,字典学习可以被简化为一个“构造工具字典”、“查阅字典”的两个过程。对于“构造工具字典”这一过程,对字典有以下几点要求:
- 字典内容尽可能全面,总结出的字典不应该漏掉数据的关键信息。
- 字典应该尽可能简洁,即快而准。
- 在占用较小资源前提下尽可能还原知识的特性。
1.3 字典学习的数学模型
更加完整的数学公式推导可以查阅博客【4】
2 python实现
2.1字典学习
实际上,就是实现了对原始信号的稀疏重构,类似于压缩感知,这里指定变换算法为“lasso lars”, 实际上,还包含以下几种:
-
‘lars’: uses the least angle regression method (lars_path);
-
‘lasso_lars’: uses Lars to compute the Lasso solution.
-
‘lasso_cd’: uses the coordinate descent method to compute the Lasso solution (Lasso). ‘lasso_lars’ will be faster if the estimated components are sparse.
-
‘omp’: uses orthogonal matching pursuit to estimate the sparse solution.
-
‘threshold’: squashes to zero all coefficients less than alpha from the projection dictionary * X’.
import numpy as np
from sklearn.datasets import make_sparse_coded_signal
from sklearn.decomposition import DictionaryLearning
X, dictionary, code = make_sparse_coded_signal(
n_samples=100, n_components=15, n_features=20, n_nonzero_coefs=10,
random_state=42, data_transposed=False
)
dict_learner = DictionaryLearning(
n_components=15, transform_algorithm='lasso_lars', transform_alpha=0.1,
random_state=42,
)
X_transformed = dict_learner.fit_transform(X)
2.1 稀疏性统计和误差计算
print("sparsity: {}".format(np.mean(X_transformed == 0)))
X_hat = X_transformed @ dict_learner.components_
print(np.mean(np.sum((X_hat - X) ** 2, axis=1) / np.sum(X ** 2, axis=1)))
结果
sparsity: 0.4633333333333333
error: 0.011433365697744878
Process finished with exit code 0
参考资料和文献
【1】 https://scikit-learn.org/stable/modules/generated/sklearn.decomposition.DictionaryLearning.html
【2】http://thoth.inrialpes.fr/people/mairal/spams/documentation.html
【3】https://stats.stackexchange.com/questions/289075/what-is-the-smallest-lambda-that-gives-a-0-component-in-lasso
【4】https://www.cnblogs.com/endlesscoding/p/10090866.html

![[附源码]java毕业设计大学生足球预约信息](https://img-blog.csdnimg.cn/39b0ca75106e4c418606d0ace5c02f93.png)