说明
【跟月影学可视化】学习笔记。
三维仿射变换:平移
对于平移变换来说,如果向量 P( x 0 x_0 x0, y 0 y_0 y0, z 0 z_0 z0) 沿着向量 Q( x 1 x_1 x1, y 1 y_1 y1, z 1 z_1 z1) 平移,只需要让 P 加上 Q,就能得到变换后的坐标。
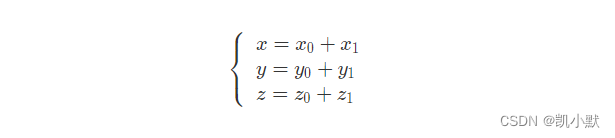
三维仿射变换:缩放
让三维向量乘上标量,就相当于乘上要缩放的倍数。
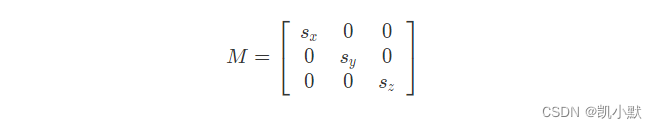
可以使用齐次矩阵来表示三维仿射变换,通过引入一个新的维度,就可以把仿射变换转换为齐次矩阵的线性变换。
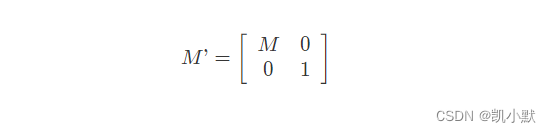
三维物体的旋转变换比较复杂一点,下面先了解一下欧拉角。
什么是欧拉角?
中文维基百科:欧拉角
莱昂哈德·欧拉用欧拉角来描述刚体在三维欧几里得空间的取向。对于任何参考系,一个刚体的取向,是依照顺序,从这参考系,做三个欧拉角的旋转而设定的。所以,刚体的取向可以用三个基本旋转矩阵来决定。换句话说,任何关于刚体旋转的旋转矩阵是由三个基本旋转矩阵复合而成的。
比如飞机的姿态可以由这三个欧拉角来确定,绕 x 轴的旋转角度(翻滚机身)、绕 y 轴的旋转角度(俯仰),以及绕 z 轴的旋转角度(偏航)来表示。
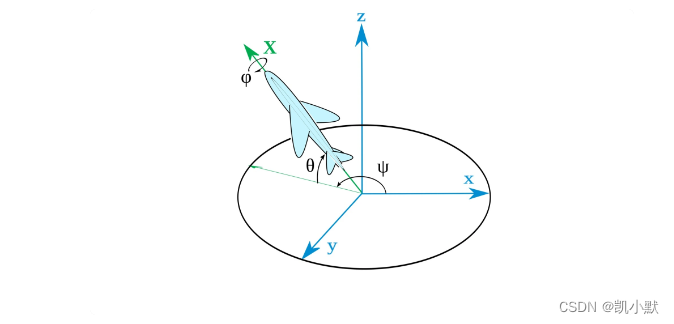
具体的表示公式就是 Rx、Ry、Rz,这三个旋转矩阵相乘。
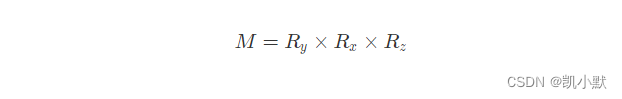
这里采用的是 y−x−z 顺规。
下面是欧拉角的顺规表示方式:
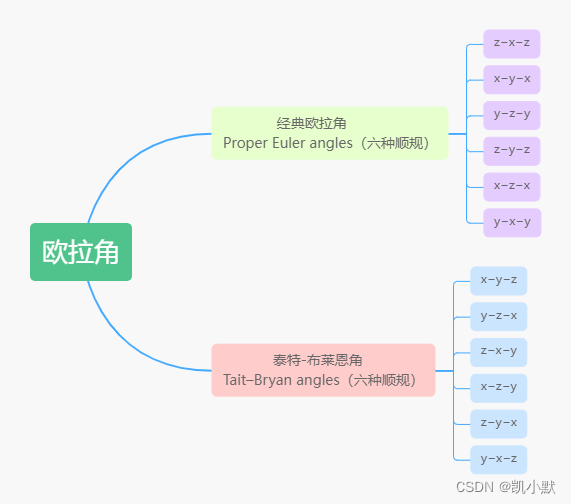
采用 y−x−z 顺规的欧拉角得到的旋转矩阵如下:

使用欧拉角来旋转几何体
让几何体绕 y 轴、x 轴、z 轴转过 α、β、γ 角。
下面是三维物体的旋转变换矩阵:
绕y轴旋转变换矩阵:
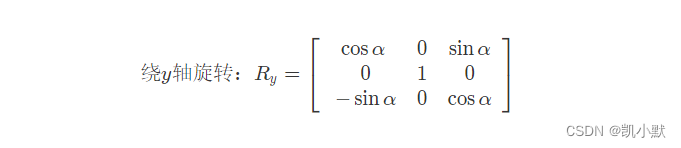
绕x轴旋转变换矩阵:
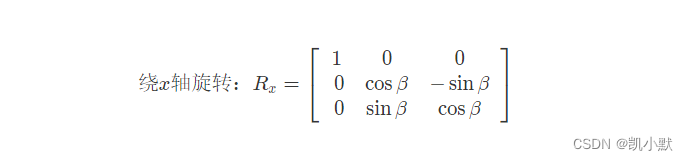
绕z轴旋转变换矩阵:
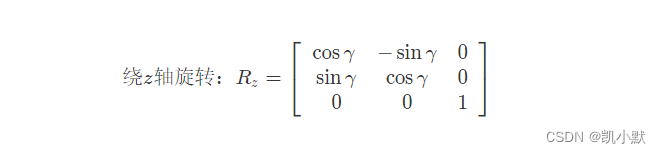
如何使用欧拉角来旋转几何体?
OGL 框架的几何网格(Mesh)对象直接支持欧拉角(默认欧拉角顺规是 y−x−z),用对象的 rotation 属性(它是一个三维向量)就可以设置欧拉角。
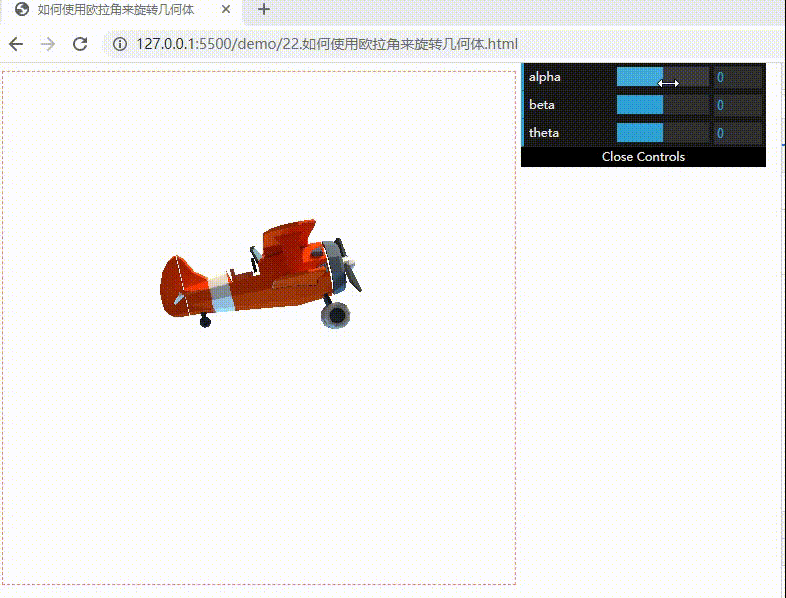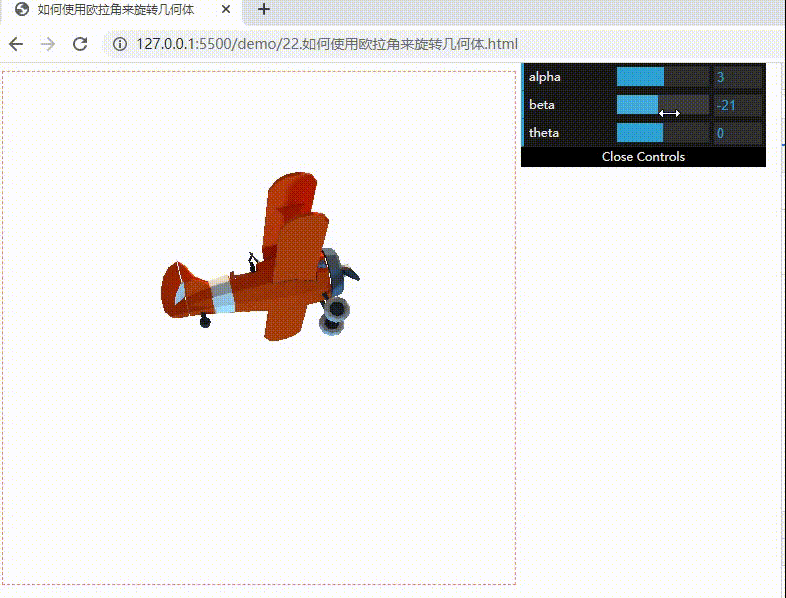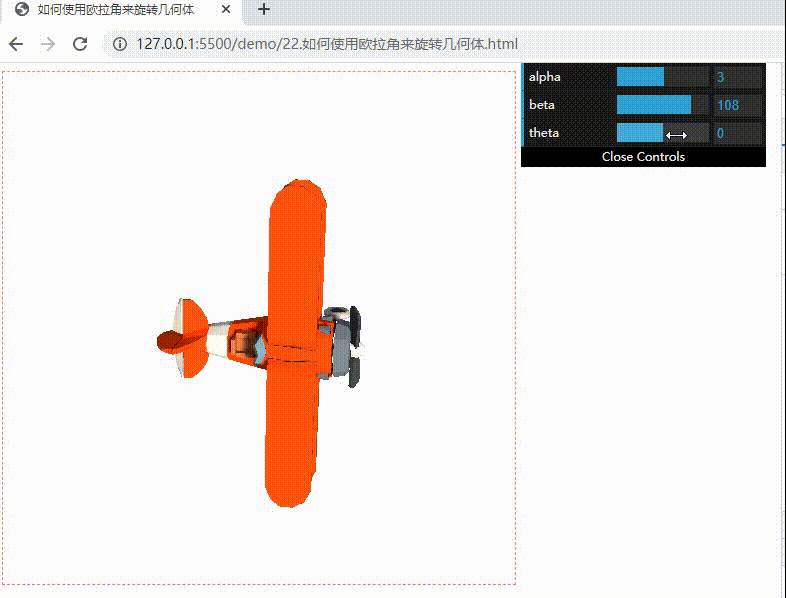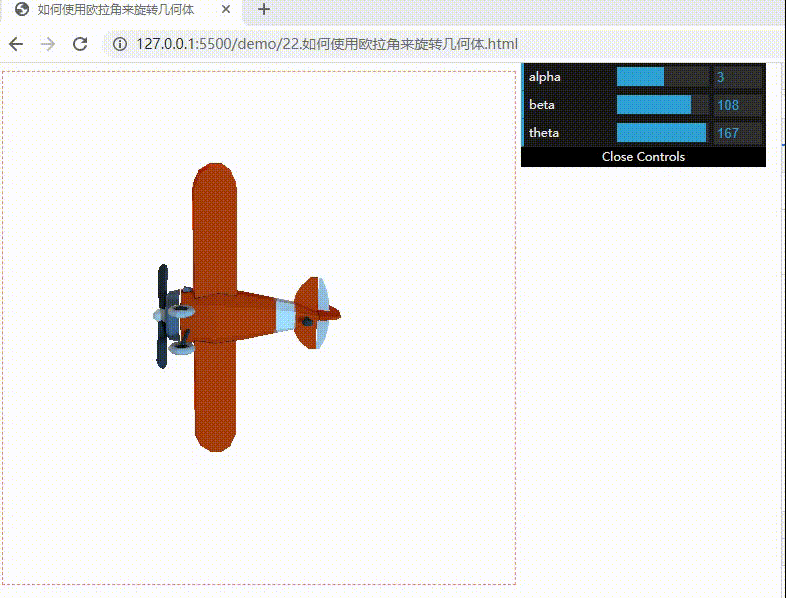
下面实现可以随意调整欧拉角的飞机模型效果:偏航(改变 alpha)、翻滚(改变 beta)和俯仰(改变 theta)
需要用到的资源
- 飞机模型json跟图片
- dat-gui:JavaScript Controller Library
<!DOCTYPE html>
<html lang="en">
<head>
<meta charset="UTF-8" />
<meta http-equiv="X-UA-Compatible" content="IE=edge" />
<meta name="viewport" content="width=device-width, initial-scale=1.0" />
<title>如何使用欧拉角来旋转几何体</title>
<style>
canvas {
border: 1px dashed rgb(250, 128, 114);
}
</style>
</head>
<body>
<canvas width="512" height="512"></canvas>
<script type="module">
import { Renderer, Camera, Transform, Geometry, Texture, Program, Mesh} from './common/lib/ogl/index.mjs';
// JavaScript Controller Library
import * as dat from './common/lib/dat.gui.js';
console.log(dat)
const canvas = document.querySelector('canvas');
const renderer = new Renderer({
canvas,
width: 512,
height: 512,
});
const gl = renderer.gl;
gl.clearColor(1, 1, 1, 1);
const camera = new Camera(gl, {fov: 35});
camera.position.set(0, 0, 10);
camera.lookAt([0, 0, 0]);
const scene = new Transform();
const vertex = `
precision highp float;
attribute vec3 position;
attribute vec3 normal;
attribute vec2 uv;
uniform mat4 modelViewMatrix;
uniform mat4 projectionMatrix;
varying vec2 vUv;
void main() {
vUv = uv;
gl_Position = projectionMatrix * modelViewMatrix * vec4(position, 1.0);
}
`;
const fragment = `
precision highp float;
uniform sampler2D tMap;
varying vec2 vUv;
void main() {
gl_FragColor = texture2D(tMap, vUv);
}
`;
// 加载模型
async function loadModel(src) {
const data = await (await fetch(src)).json();
// 创建 Geometry 对象,并返回这个对象
const geometry = new Geometry(gl, {
position: {size: 3, data: new Float32Array(data.position)},
uv: {size: 2, data: new Float32Array(data.uv)},
normal: {size: 3, data: new Float32Array(data.normal)},
});
return geometry;
}
// 加载纹理
function loadTexture(src) {
const texture = new Texture(gl);
return new Promise((resolve) => {
const img = new Image();
img.onload = () => {
texture.image = img;
resolve(texture);
};
img.src = src;
});
}
(async function () {
// 加载飞机几何体模型
const geometry = await loadModel('./assets/model/airplane.json');
// 加载飞机的纹理图片
const texture = await loadTexture('./assets/model/airplane.jpg');
// 渲染部分
const program = new Program(gl, {
vertex,
fragment,
uniforms: {
tMap: {value: texture},
},
});
const mesh = new Mesh(gl, {geometry, program});
mesh.setParent(scene);
renderer.render({scene, camera});
// 添加控制
const gui = new dat.GUI();
const palette = {
alpha: 0,
beta: 0,
theta: 0,
};
gui.add(palette, 'alpha', -180, 180).onChange((val) => {
mesh.rotation.y = val / 180 * Math.PI;
renderer.render({scene, camera});
});
gui.add(palette, 'beta', -180, 180).onChange((val) => {
mesh.rotation.x = val / 180 * Math.PI;
renderer.render({scene, camera});
});
gui.add(palette, 'theta', -180, 180).onChange((val) => {
mesh.rotation.z = val / 180 * Math.PI;
renderer.render({scene, camera});
});
}());
</script>
</body>
</html>
效果如下:
如何理解万向节锁?
使用欧拉角来操作几何体的方向有个缺陷叫做万向节锁 (Gimbal Lock)。
什么是 Gimbal ?
平衡环架(英语:Gimbal),是一具有枢纽的装置,作用是使得一物体能以单一轴旋转。由彼此垂直的枢纽轴所组成的一组三只平衡环架,则可使架在最内的环架的物体维持旋转轴不变,而应用在船上的陀螺仪、罗盘、饮料杯架等用途上,而不受船体因波浪上下震动、船身转向的影响。
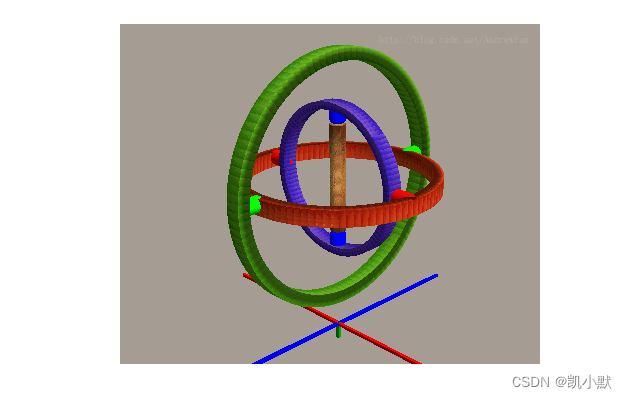
什么是万向节锁 (Gimbal Lock) ?
在特定的欧拉角情况下,姿态调整的自由度丢失就是万向节锁 (Gimbal Lock) 。
我们调整 beta 的角度改成 90,不管改变 alpha 还是改变 theta,飞机都绕着 y 轴旋转,始终处于一个平面上。本来飞机姿态有 x、y、z 三个自由度,现在 y 轴被固定了,只剩下两个自由度了,这就是万向节锁。
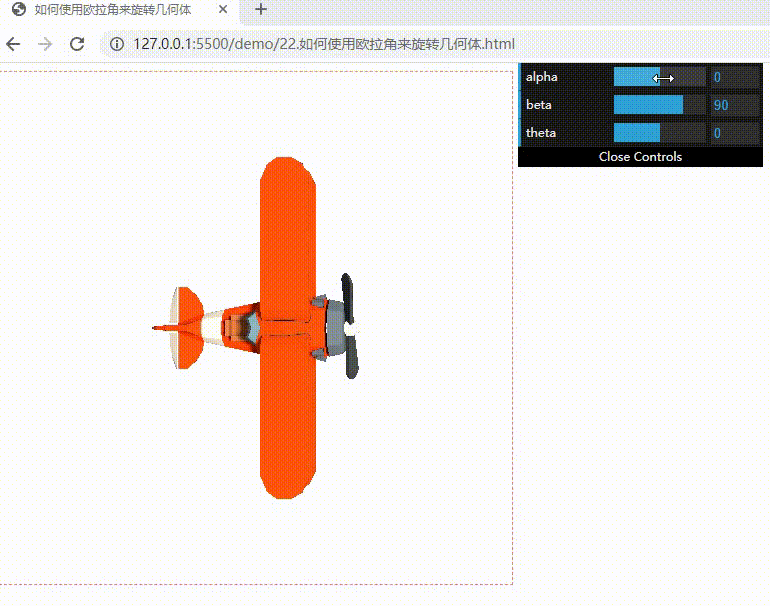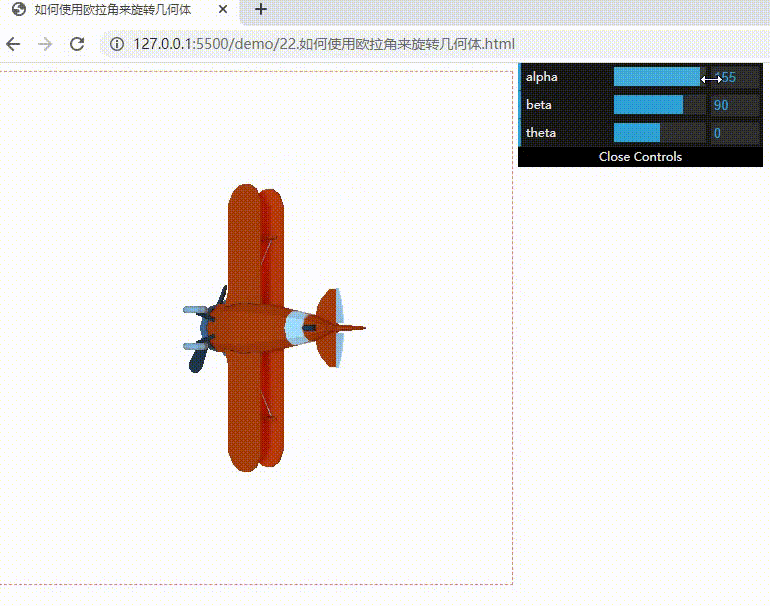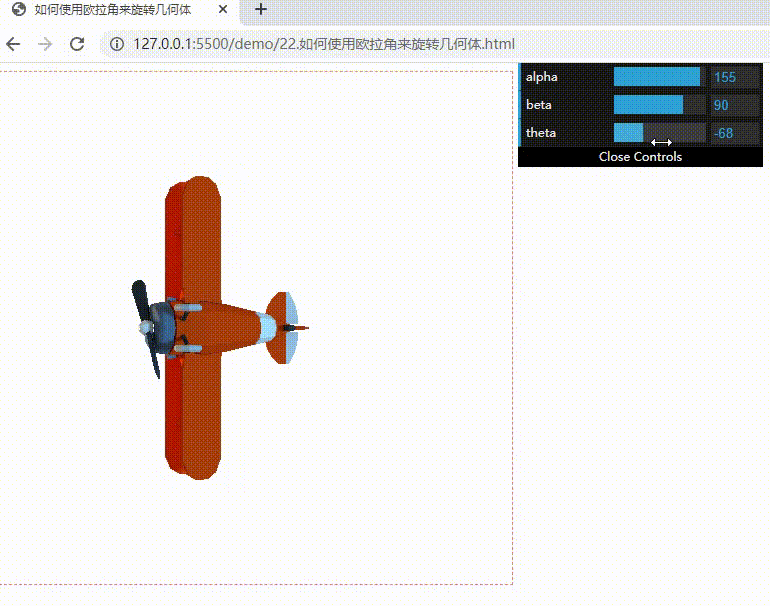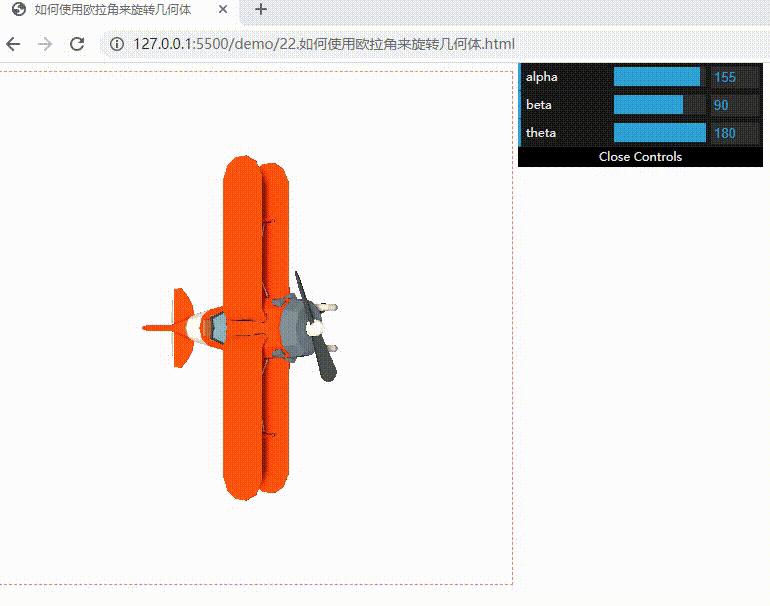
要避免万向节锁的产生,可以使用比较好的一种数学模型:四元数(Quaternion)。
使用四元数来旋转几何体
四元数是一种高阶复数,一个四元数可以表示为:q = w + xi + yj + zk。
- i、j、k 是三个虚数单位,w 是标量
- 满足 i 2 i^2 i2 = j 2 j^2 j2 = k 2 k^2 k2 = ijk = −1
所谓单位四元数,就是其中的参数满足 x 2 x^2 x2+ y 2 y^2 y2+ z 2 z^2 z2+ w 2 w^2 w2=1。单位四元数对应的旋转矩阵如下:
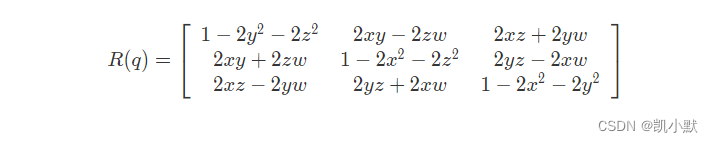
四元数与轴角
所谓轴角,就是在三维空间中,给定一个由单位向量表示的轴,以及一个旋转角度 ⍺,以此来表示几何体绕该轴旋转 ⍺ 角。
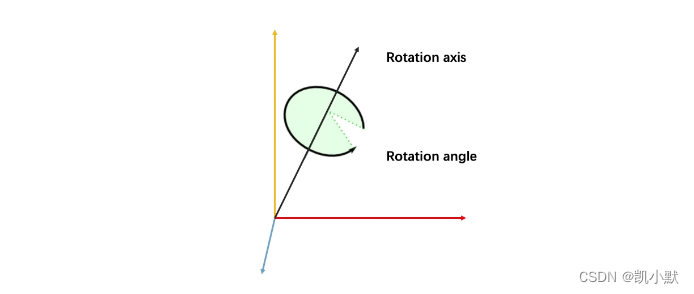
绕单位向量 u 旋转 ⍺ 角,对应的四元数可以表示为:q = (usin(⍺/2), cos(⍺/2))。
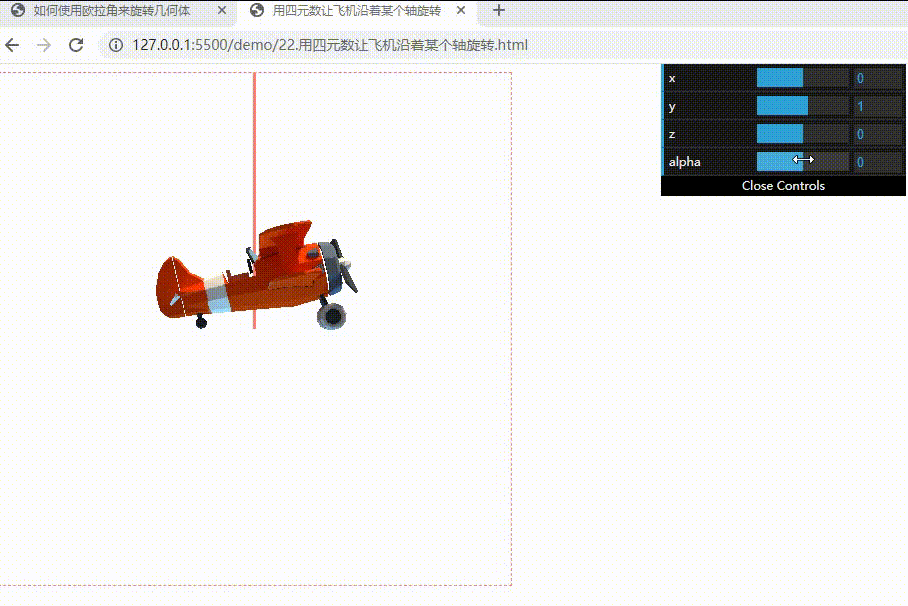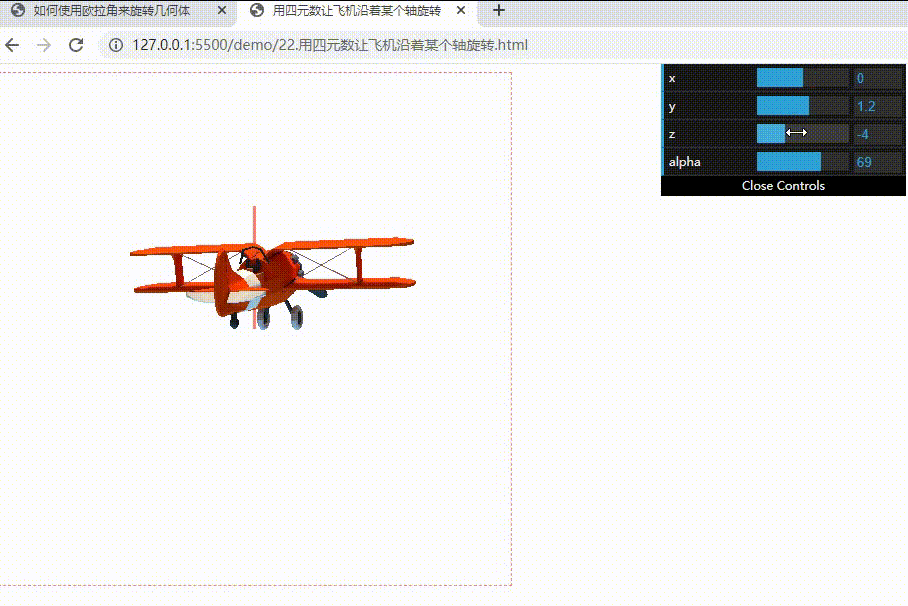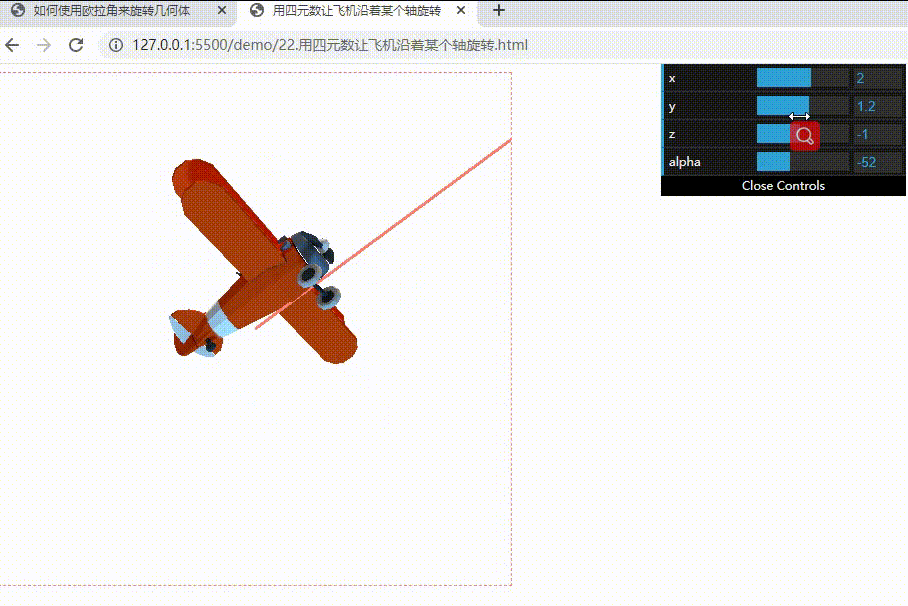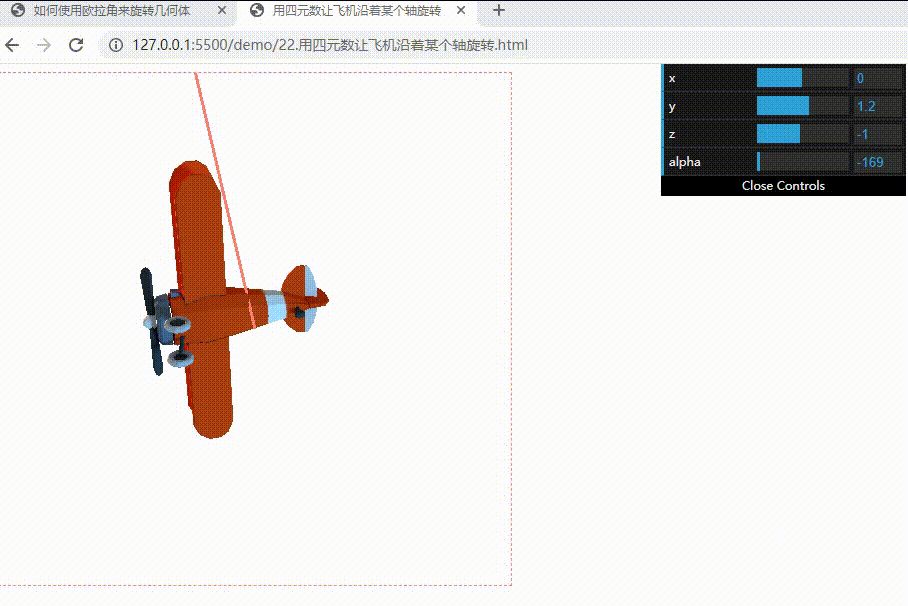
下面实现一下用四元数让飞机沿着某个轴旋转:
<!DOCTYPE html>
<html lang="en">
<head>
<meta charset="UTF-8" />
<meta http-equiv="X-UA-Compatible" content="IE=edge" />
<meta name="viewport" content="width=device-width, initial-scale=1.0" />
<title>用四元数让飞机沿着某个轴旋转</title>
<style>
canvas {
border: 1px dashed #fa8072;
}
</style>
</head>
<body>
<canvas width="512" height="512"></canvas>
<script type="module">
import { Renderer, Camera, Transform, Geometry, Texture, Orbit, Program, Mesh, Polyline } from './common/lib/ogl/index.mjs';
import { Vec3 } from "./common/lib/math/vec3.js";
import { Quat } from "./common/lib/math/Quat.js";
import { Color } from "./common/lib/math/Color.js";
// JavaScript Controller Library
import * as dat from './common/lib/dat.gui.js';
console.log(dat)
const canvas = document.querySelector('canvas');
const renderer = new Renderer({
canvas,
width: 512,
height: 512,
});
const gl = renderer.gl;
gl.clearColor(1, 1, 1, 1);
const camera = new Camera(gl, {fov: 35});
camera.position.set(0, 0, 10);
camera.lookAt([0, 0, 0]);
const scene = new Transform();
const vertex = `
precision highp float;
attribute vec3 position;
attribute vec3 normal;
attribute vec2 uv;
uniform mat4 modelViewMatrix;
uniform mat4 projectionMatrix;
varying vec2 vUv;
void main() {
vUv = uv;
gl_Position = projectionMatrix * modelViewMatrix * vec4(position, 1.0);
}
`;
const fragment = `
precision highp float;
uniform sampler2D tMap;
varying vec2 vUv;
void main() {
gl_FragColor = texture2D(tMap, vUv);
}
`;
// 加载模型
async function loadModel(src) {
const data = await (await fetch(src)).json();
// 创建 Geometry 对象,并返回这个对象
const geometry = new Geometry(gl, {
position: {size: 3, data: new Float32Array(data.position)},
uv: {size: 2, data: new Float32Array(data.uv)},
normal: {size: 3, data: new Float32Array(data.normal)},
});
return geometry;
}
// 加载纹理
function loadTexture(src) {
const texture = new Texture(gl);
return new Promise((resolve) => {
const img = new Image();
img.onload = () => {
texture.image = img;
resolve(texture);
};
img.src = src;
});
}
const controls = new Orbit(camera);
(async function () {
// 加载飞机几何体模型
const geometry = await loadModel('./assets/model/airplane.json');
// 加载飞机的纹理图片
const texture = await loadTexture('./assets/model/airplane.jpg');
// 渲染部分
const program = new Program(gl, {
vertex,
fragment,
uniforms: {
tMap: {value: texture},
},
});
const mesh = new Mesh(gl, {geometry, program});
mesh.setParent(scene);
// 定义轴,通过 Polyline 对象来绘制轴。
const points = [
new Vec3(0, 0, 0),
new Vec3(0, 10, 0),
];
const axis = new Polyline(gl, {
points,
uniforms: {
uColor: {value: new Color("#fa8072")},
uThickness: {value: 3},
},
});
axis.mesh.setParent(scene);
renderer.render({scene, camera});
// 添加控制
const gui = new dat.GUI();
const palette = {
alpha: 0,
x: 0,
y: 1,
z: 0
};
// 更新轴
function updateAxis() {
const {x, y, z} = palette;
const v = new Vec3(x, y, z).normalize().scale(10);
points[1].copy(v);
axis.updateGeometry();
renderer.render({scene, camera});
}
// 更新四元数
function updateQuaternion(val) {
const theta = 0.5 * val / 180 * Math.PI;
const c = Math.cos(theta);
const s = Math.sin(theta);
const p = new Vec3().copy(points[1]).normalize();
const q = new Quat(p.x * s, p.y * s, p.z * s, c);
mesh.quaternion = q;
renderer.render({scene, camera});
}
gui.add(palette, 'x', -10, 10).onChange(updateAxis);
gui.add(palette, 'y', -10, 10).onChange(updateAxis);
gui.add(palette, 'z', -10, 10).onChange(updateAxis);
gui.add(palette, 'alpha', -180, 180).onChange(updateQuaternion);
}());
</script>
</body>
</html>
拓展阅读
- 四元数与三维旋转
- 三维旋转:欧拉角、四元数、旋转矩阵、轴角之间的转换

![[附源码]JAVA毕业设计高校智能排课系统(系统+LW)](https://img-blog.csdnimg.cn/880302af841b47af92df7b388dd2ff77.png)





![[附源码]Python计算机毕业设计Django二次元信息分享平台的设计及实现](https://img-blog.csdnimg.cn/ceff51a9d2b549e690789410cb254629.png)