目录
一、直接插入排序
二、折半插入排序
三、希尔排序
四、冒泡排序
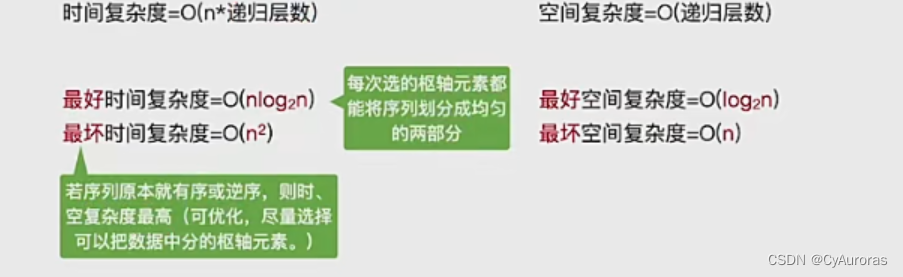
五、快速排序
*效率分析
一、直接插入排序
思想:每次将一个待排序的记录按其关键字大小插入到前面已经排好序中,直到全部记录插入完毕
保证稳定性
空间复杂度:O(1)
时间复杂度:![]()

void InsertSort(int A[],int n){
int i,j,temp;
for(i=1;i<=n;i++)
if(A[i]<A[i-1]){
temp=A[i];
for(j=i-1;j>=0 && A[j]>temp;--j)
A[j+1]=A[j];
A[j+1]=temp;
}
}二、折半插入排序
思想:先用折半查找找到应该插入的位置,再移动元素
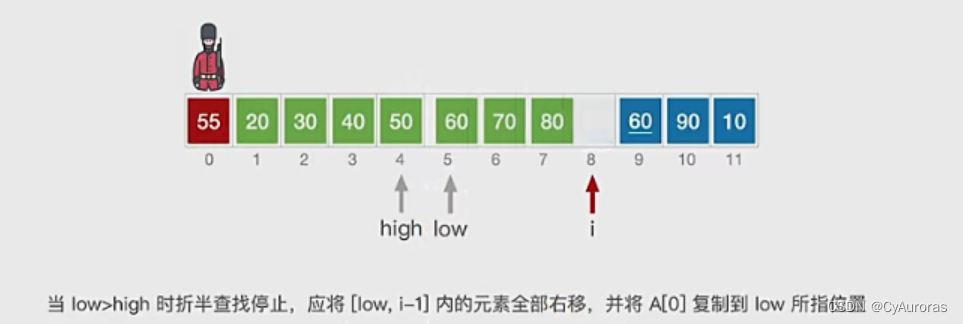
保证稳定性
空间复杂度:O(1)
时间复杂度:![]()
void InsertSort(int A[],int n){
int i,j,low,high,mid;
for(i=2;i<=n;i++){
A[0]=A[i];
low=1;high=i-1;
while(low<high){
mid=(low+high)/2;
if(A[mid]>A[0])
high=mid-1;
else
low=mid+1;
}
for(j=i-1;j>=high+1;--j)
A[j+1]=A[j];
A[high+1]=A[0];
}
}三、希尔排序

第一趟:d1=n/2=5
第二趟:d2=d1/2=3 向上取整

不稳定性
空间复杂度:O(1)
时间复杂度:
void ShellSort(int A[],int n){
int d,i;
for(d=n/2;d>1=1;d=d/2){
for(i=d+1;i<=n;++i){
if(A[i]<A[i-d]){
A[0]=A[i];
for(j=i-d;j>0 && A[0]<A[j];j-=d){
A[j+d]=A[i];
}
A[j+d]=A[0];
}
}
}
}四、冒泡排序
思想:从后往前(或从前往后)两两比较相邻元素值,A[i-1]>A[i]就交换它们,直到序列比较完,称一趟排序
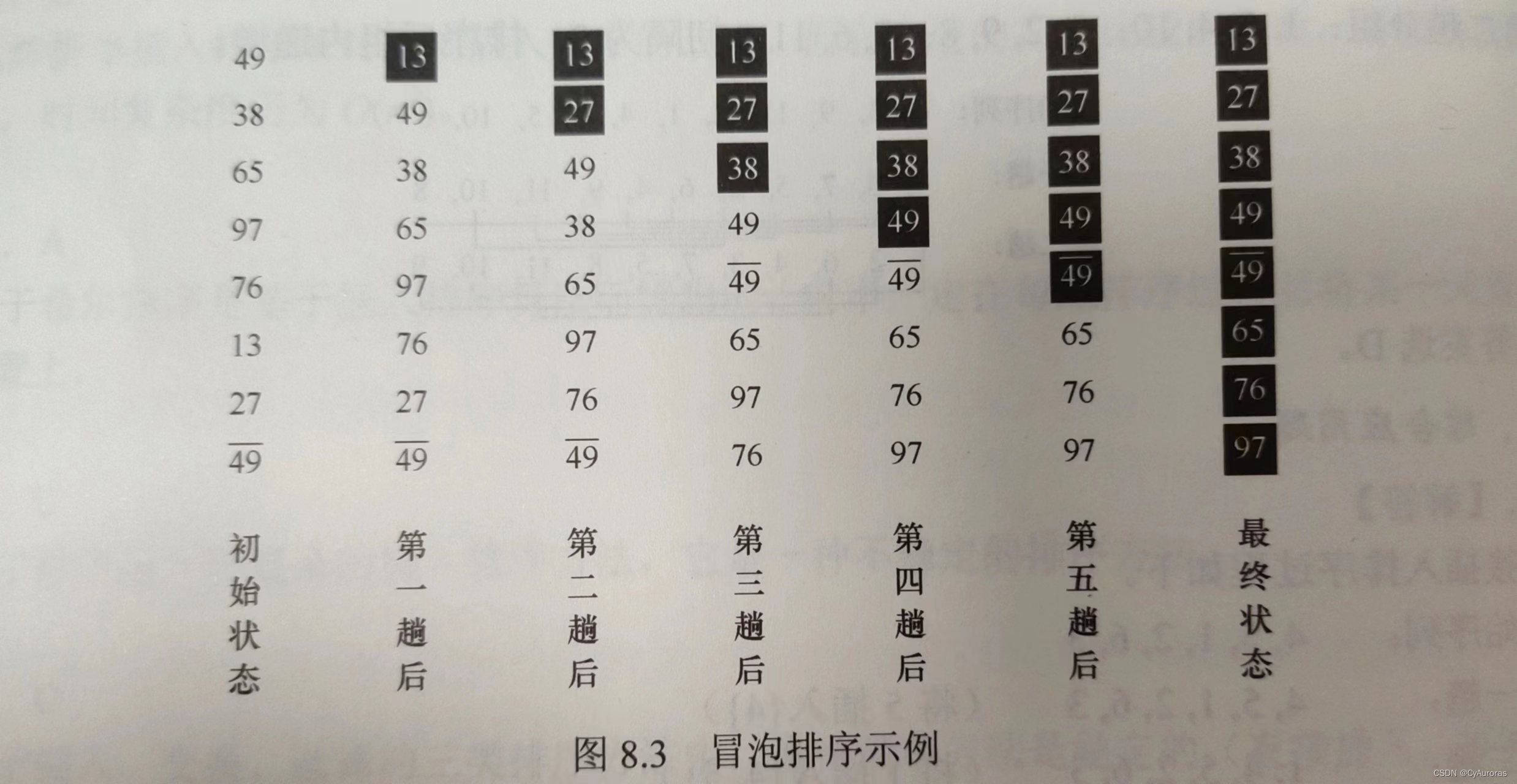
保证稳定性
空间复杂度:O(1)
时间复杂度:![]()
void swap(int &a,int &b){
int temp=a;
a=b;
b=temp;
}
void BubbleSort(int A[],int n){
for(int i=0;i<n-1;i++){
bool flag=false;
for(int j=n-1;j<i;j--)
if(A[j-1]>A[j]){
swap(A[j-1],A[j]);
flag=true;
}
if(flag=true)
return;
}
}五、快速排序

基准
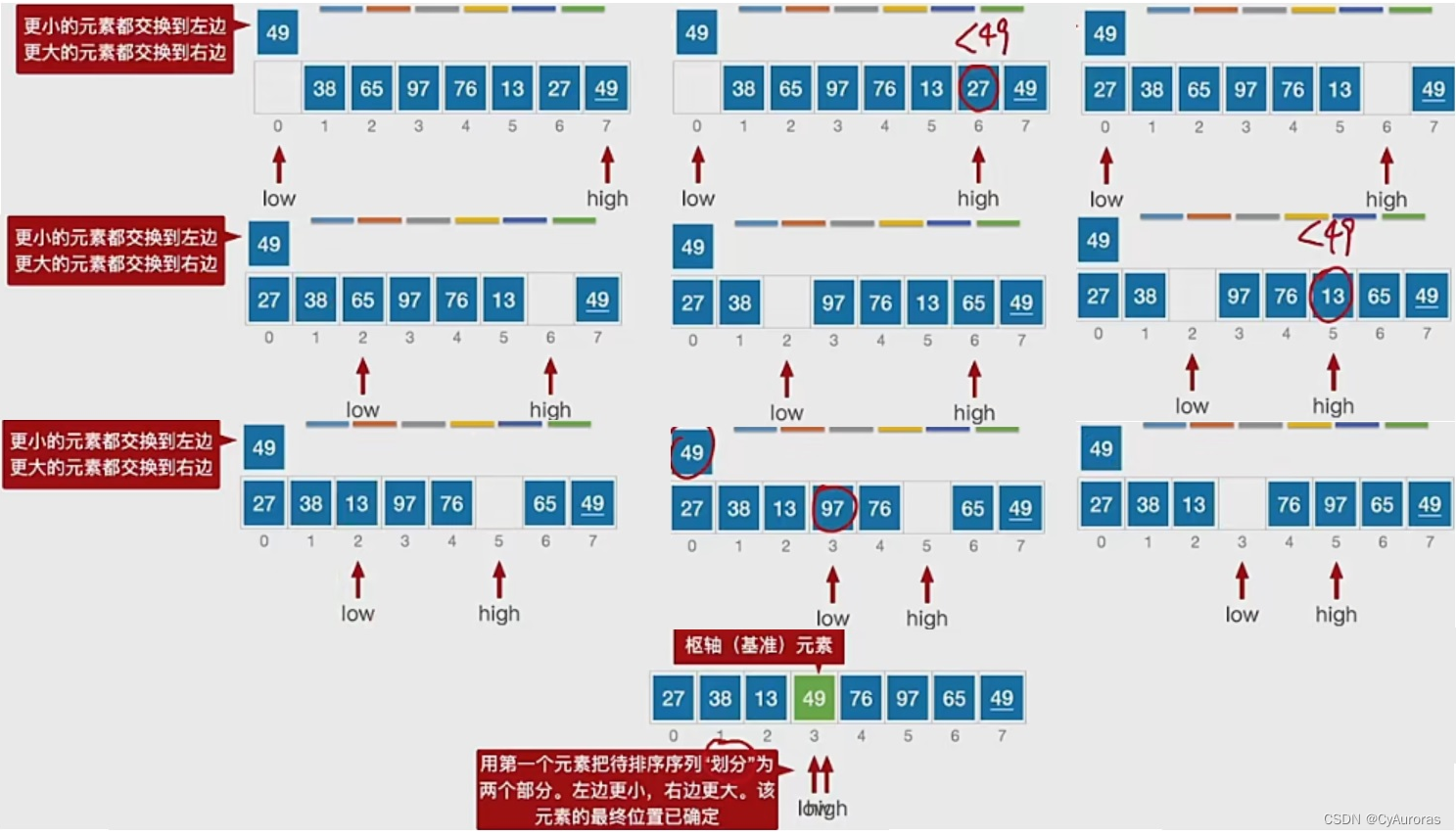
不稳定性
//用第一个元素将待排序序列划分成左右两个部分
int Partition(int A[],int low,int high){
int pivot=A[low]; //第一个元素为基准元素
while(low<high){ //用low和high搜索基准的最终位置
while(low<high&&A[high]>=pivot) --high;
A[low]=A[high]; //比基准元素小的移动到左边
while(low<gigh&&A[low])<=pivot) ++low;
A[high]=A[low]; //比基准元素大的移动到右边
}
A[low]=pivot; //基准元素存放到最终位置
return low; //返回存放的最终位置
}
//快速排序
void QuickSOrt(int A[],int n){
if(low<high){ //递归跳出的条件
int pivotpos=Partition(A,low,high); //划分
QuickSOrt(A,low,pivotpos-1); //划分左子树
QuickSOrt(A,pivotpos+1,high); //划分右子树
}
}*效率分析
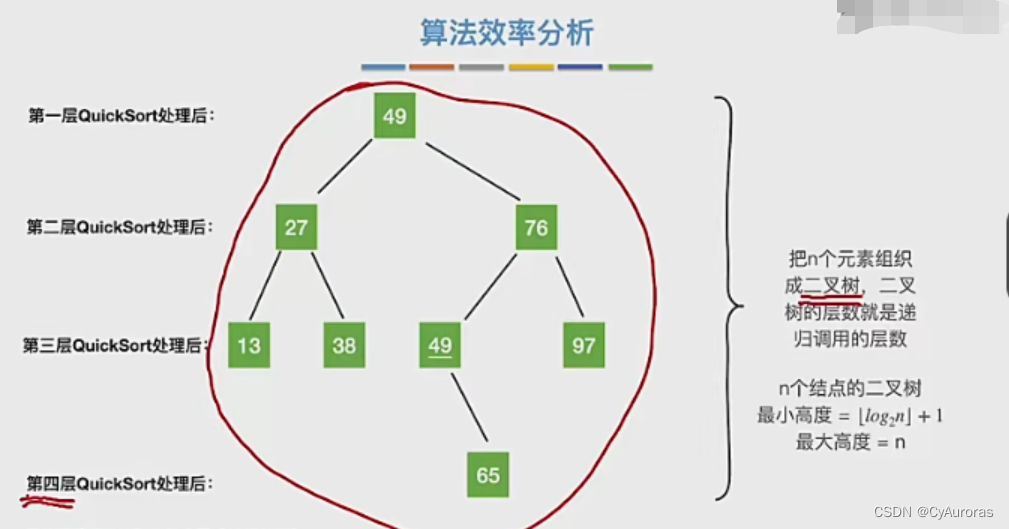







![PMP项目管理-[第十一章]风险管理](https://img-blog.csdnimg.cn/a4b3f502a3554c43a0c8d9e75547dd19.png)



![[数据集][目标检测]篮球数据集VOC格式7398张](https://i2.hdslb.com/bfs/archive/fc56600314ed0869f21da32f4d9837fef9eb17d6.jpg@100w_100h_1c.png@57w_57h_1c.png)

