Problem - D - Codeforces

 

威廉来到了一个专门讨论加密货币的会议。要想了解加密货币世界的最新消息，建立联系、认识新朋友、利用朋友的关系是必不可少的。

会议有N个参与者，他们最初都不熟悉对方。威廉可以把之前不熟悉的任何两个人a和b介绍给对方。

威廉有d个条件，其中第i个条件要求人xi与人yi有联系。从形式上看，如果有这样一条链p1=x,p2,p3,...,pk=y，对于1到k-1的所有i来说，编号为pi和pi+1的两个人确实认识对方，则两个人有联系。

对于每一个i（1≤i≤d），威廉希望你能计算出一个人能够拥有的最大的熟人数量，假设威廉满足了从1到i（包括i）的所有条件，并且正好进行了i次介绍。这些条件是在威廉进行了i次介绍之后被检查出来的。每个i的答案必须独立计算。这意味着，当你计算i的答案时，你应该假设还没有两个人被介绍给对方。

输入
第一行包含两个整数n和d（2≤n≤103,1≤d≤n-1），分别是人的数量和条件的数量。

接下来的d行各包含两个整数xi和yi (1≤xi,yi≤n,xi≠yi)，根据条件i必须有联系的人数。

输出
如果William进行了i次介绍并满足了前i个条件，则第i个数字必须等于拥有最大可能的熟人的人数。

例子
输入复制
7 6
1 2
3 4
2 4
7 6
6 5
1 7
输出拷贝
1
1
3
3
3
6
输入复制
10 8
1 2
2 3
3 4
1 4
6 7
8 9
8 10
1 4
输出拷贝
1
2
3
4
5
5
6
8
备注
对第一个测试案例的解释。

在这个解释中，圆圈和其中的数字表示具有相应数字的人。这条线表示威廉介绍了两个有联系的人。标记为红色的人有最多的熟人。这些并不是介绍人的唯一正确方法。

题解:
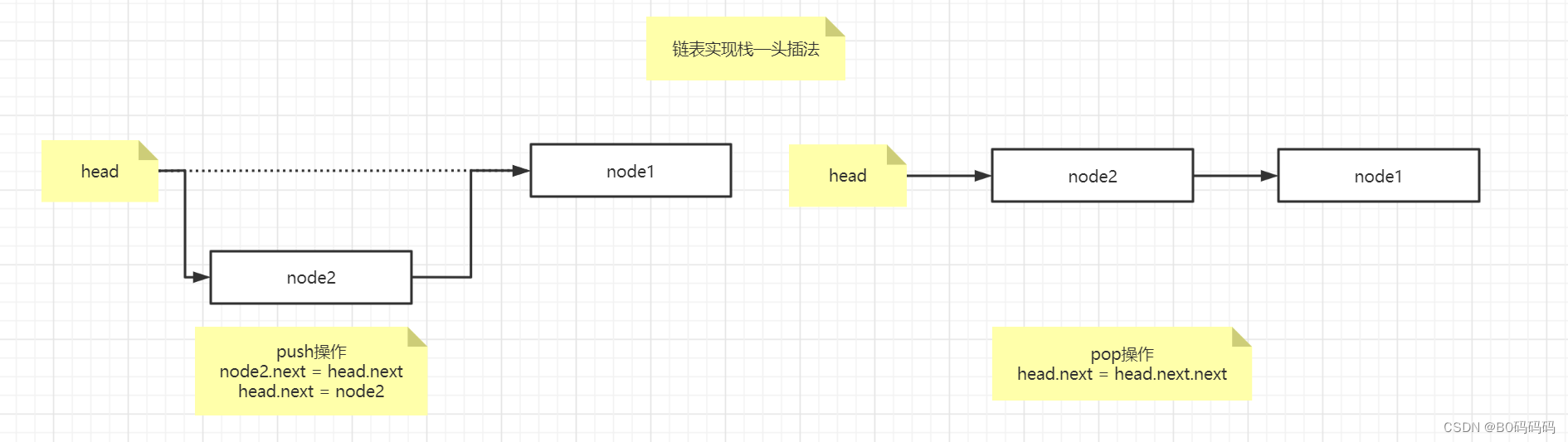
我们每次并查集找x,y是否连接

如果未连接,我们就应该让他们连接上,清空其中一个块的数目,加到另一个块上,并且连接他们

如果已经连接.那我们就有额外一次连接机会k++(初始为1),排序找到前k个最大的相加ans

答案为ans - 1

#include<iostream>
#include<vector>
#include<queue>
#include<cstring>
#include<algorithm>
#include<string>
#include<map>
using namespace std;
#define int long long
int f[1030];
int siz[1030];
int w[1030];
int find(int x)
{
	if(f[x] == x)
	return x;
	return f[x] = find(f[x]);
}
void solve()
{
	ios::sync_with_stdio(false);
	cin.tie(0);
	cout.tie(0);
	int n,m;
	cin >> n >>m;
	for(int i = 1;i <= n;i++)
	{
		f[i] = i;
		siz[i] = 1;
	}
	int cnt = 1;
	while(m--)
	{
		int x,y;
		cin >> x >> y;
		if(find(x) == find(y))
		{
			cnt++;
		}
		else
		{
			siz[find(x)] += siz[find(y)];
			siz[find(y)] = 0;
			f[find(y)] = find(x);
		}
		for(int i = 1;i <= n;i++)
		{
			w[i] = siz[i];
		}
		sort(w+1,w+1+n,greater<int>());
		int ans = 0;
		for(int i = 1;i <= cnt;i++)
		{
			ans += w[i];
		}
		cout<<ans-1<<"\n";
	}
}
signed main()
{
	int t = 1;
//	cin >> t;
	while(t--)
	{
		solve();
	}
}