申明： 未经许可，禁止以任何形式转载，若要引用，请标注链接地址。 全文共计7685字，阅读大概需要3分钟
更多学习内容， 欢迎关注我的个人公众号：不懂开发的程序猿

学习目标

1 Decision Tree Based Intrusion Detection System for NSL-KDD Dataset

2 一种用于入侵检测的自适应集成机器学习模型

3 一种由GA和SVM组成的混合方法，用于入侵检测系统

学习内容

一．Decision Tree Based Intrusion Detection System for NSL-KDD Dataset

从 NSL-KDD 数据集的数据集存储库中选择数据集。之后，对所选数据应用预处理，以将非数值属性转换为数值。在下一步中，特征选择方法应用于降维。应用随机抽样来摆脱偏倚训练。接下来的三个步骤定义了CART(Classification and Regression Tree)算法，它包括树诱导，树修剪和使用新的测试数据集测试生成的树。CART 是递归分区算法，它通过在每个节点上拆分来构建二叉决策树。决策树的根节点包含完整的训练样本。在最后一步中，使用各种性能参数（如分类准确性、检测率和误报率）评估性能。

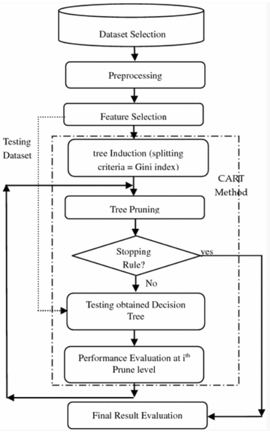
决策树⽤于对具有共同属性的数据进行分类。⽤于量化信息的概念称为熵，⽤于衡量数据集的随机性数量。当⼀个集合中的所有数据都属于⼀个类时，没有不确定性，那么熵为零。决策树分类的⽬标是将给定的数据集迭代地划分为⼦集，其中每个最终⼦集中的所有元素都属于同⼀类。熵计算如公式 1 所⽰。给定数据集中不同类别的概率p1, p2,…,ps
$$Entropy:H(p_1,p_2,...,p_s)=\sum _{i=1}^s(p_{i}log(\frac{1}{p_i}))$$
给定⼀个数据集 D, H(D)在数据集的基于类的⼦集中找到熵的数量。

当使⽤某个属性将该⼦集拆分为 s 个新⼦集S = {D1, D2,…,Ds}时，我们可以再次查看这些⼦集的熵。数据集的⼦集是完全有序的，如果其中的所有⽰例都属于同⼀类，则不需要进⼀步拆分。 ID3 算法使⽤等式 2 计算拆分的信息增益，并选择提供最⼤信息增益的拆分。
$$Gain(D,S)=H(D)-\sum _{i=1}^{s}p(D_i)H(D_i)$$

过程：

1. 初始化D 中的所有权重， Wi=1/n，其中n是总数
2. 计算每个类Cj的先验概率P(Cj)
3. 计算P(A )的条件概率P(Aij | Cj ) D中的每个属性值
4. 计算每个例⼦的后验概率
5. ⽤后验概率P(Cj|ei)的最⼤似然 (ML) 更新D中⽰例的权重；
6. 使⽤更新后的权重Wi在D中找到具有最⾼信息增益的分裂属性。
7. T = 创建根节点和带有分割的标签属性。
8. 对于T 的每个分⽀， D = 对 D 应⽤分裂谓词创建的数据库，并继续步骤1 到 7，直到每个最终⼦集属于创建的同⼀类或叶节点。
9. 当决策树构建完成时，算法终⽌

二、一种用于入侵检测的自适应集成机器学习模型

自适应集成学习模型主要包括以下过程：

1. 输入 NSL-KDD 训练数据集。

2. 预处理模块将标签、服务等字符型特征转化为数字，对数据进行标准化，删除不必要的特征。

3. 使用预处理数据对候选算法进行集成训练。

4. 对所有算法使用训练数据进行交叉验证训练，选出检测精度和运算性能较好的算法进行投票，并对各个算法进行boost，进一步提高检测精度。boosting方法包括特征选择、不平衡采样、类权重、多层检测等。本文对决策树算法进行了优化，提出了MultiTree算法。

5. 根据各算法的训练精度，设置各算法的分类权重，生成自适应投票算法模型。

6. 输入整个 NSL-KDD 测试集的数据并在步骤 2 中对其进行预处理。

7. 选择的每个算法用于检测测试集，输出初步预测分类，然后使用自适应投票算法计算最终投票结果。

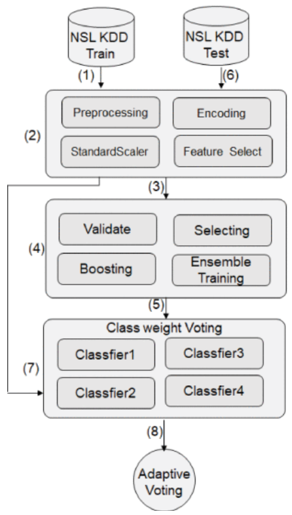
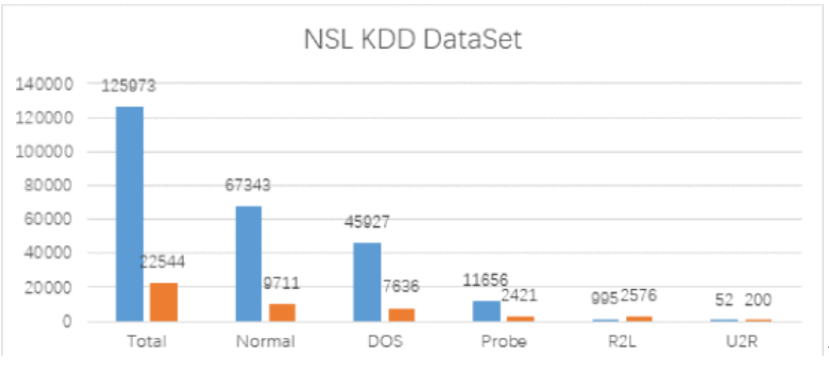
数据集：NSL-KDD

Normal 占总数据的比例最高，约占总数据的 53%，而 U2R 类型的样本数据很少，可能会导致训练不足和欠拟合。事实上，Probe、R2L 和 U2R 经常被黑客用作高级威胁攻击，因此我们应该尽最大努力提高这些类型数据的分类准确性。

数据预处理：

原始数据集中有42个字段，其中label、protocol和flag字段是字符类型。这些字段不能直接作为机器学习算法的输入，因此需要进行预处理操作。首先，将原始数据中的标签标签列转换为五种类型，Normal：0，DOS：1，Probe：2，R2L：3，U2R：4。 使用 one-Hot-Encoding 处理其文本值，将所有分类特征转换为二进制特征，在原始数据中，很多特征字段的取值范围变化很大，对训练结果影响很大。因此，Standard Scaler 方法用于对数据进行标准化。通过减去均值再除以方差（或标准差）来转换标准化数据。归一化后的数据符合标准正态分布，

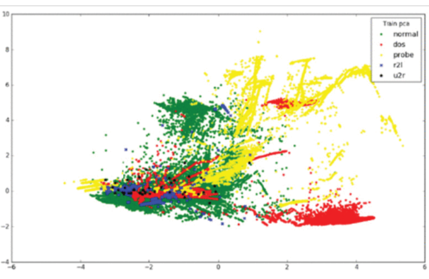
为了直观地理解数据的分布，我们将 NSL-KDD 的维度从 42 降到 2，希望 2 维数据集尽可能地代表原始数据集。主成分分析 (PCA) 用于找出数据中最重要的方面。我们可以在二维图上直观地看到数据集的分布。

由于数据集中各类数据的比例严重失衡，Normal和DOS类型占数据的比例较高，导致这些类型的准确率较高，而U2R类型的准确率较低。本文设计了一种集成算法，通过调整不同类型样本的比例来训练多个CART分类器，以解决样本比例的不平衡问题。

D. Multi-Tree算法

选择CART（分类回归树）对样本数据进行分类

如果有K个类，样本点属于的概率ķ 类是pķ ，则概率分布的基尼指数定义如下
$$Gini(p)=1-{\Sigma }_1^k{p}_k^2$$
对于给定的样本集D，其基尼指数为:
G i n i ( D ) = 1 − Σ k = 1 K { ∣ C k ∣ ∣ D ∣ } 2 Gini(D)=1-\Sigma^K_{k=1}\{ \frac {\vert C_k \vert} {\vert D \vert}\}^2 Gini(D)=1−Σk=1K​{∣D∣∣Ck​∣​}2
Cķ 是D中K类的样本子集，K是类的个数。基尼指数是类概率平方和之差。基尼指数越大，样本集的不确定性越高。分类学习过程的本质是样本不确定性的减少（即熵减少的过程），因此应该选择最小基尼指数的特征分裂

过程：

# step 1 训练第一棵决策树

rus=RandomUnderSampler(比率= {1/16*r0,r1,r2,r3,r4})

# 将Normal类型的比例降低到1/16，解决样本不平衡的问题。

Train_rus = rus.fit_sample(Train_D)

Dtree1.fit(Train_rus)

pred_y1 = Dtree1.predict(Test_D)

# step 2 训练正常和异常决策树

ConvertBinary(Train_D, Test_D)
 
# 将训练集和测试集分为两类。

rus = RandomUnderSampler（比率 = {1/8*r0,r1}）

#调整正常/异常采样率。

Train_rus2 = rus.fit_sample(Train_D)

DTree2.fit(Train_rus2)

y_normal = DTree2.predict(Test_D)

error_index = list(pred_y1 == 0).isin（list（y_normal == 1））

# 统计分类不一致的记录。记录在第一步中标识为 0，在第二步中标识为 1。

# step 3：将Step 1识别为Normal和Step 2异常的数据进一步分类为(1,2,3,4)类。

rus=RandomUnderSampler(比率 = {r1,r2,r3,r4})

#只训练攻击类型决策树
Train_rus3 = rus.fit_sample(Train_D)

DTree3.fit(Train_rus3)

error_y_ = clf_evil.predict(Test_D[error_index])

pred_y1[error_index] = error_y
#重新分配评估结果

返回 pred_y1

E. 深度神经网络(Deep Neural Networks)算法/多层感知机（Multi-Layer perceptron,MLP）

还以DNN作为基分类器算法，提高了其检测效果，模型只能用于二元分类，ReLU（Rectified Linear Unit）作为激活函数。DNN的网络结构和参数，略。

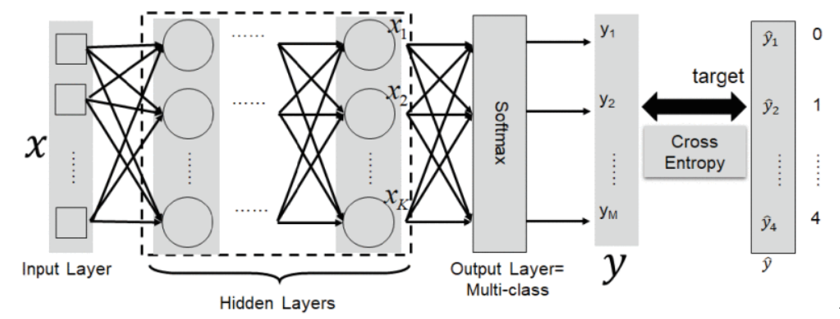
F. 自适应投票

为了综合每种算法的优点，我们提出了一种自适应投票算法。图 7 所示的算法为同一个训练集训练不同的分类器（弱分类器），然后将这些弱分类器组装成一个更强的最终分类器。该算法的核心思想是确定分类器算法对某一类数据的权重 w ij ，

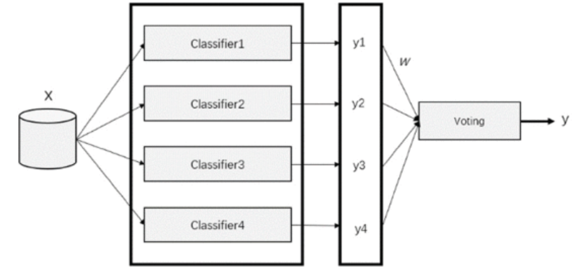
自适应投票算法如下：

1. 优化 F 中的机器学习算法（分类器），然后使用训练集和验证集对其进行训练和评估。
2. 计算每种算法针对不同攻击类型的训练准确度作为权重基数 w ij。
3. 对于每条测试记录，根据[0-4]类型计算每个分类器的预测结果。
4. 选择投票结果最大的类作为记录的最终预测结果。
5. 输出完整的五类测试结果。

1. 测试评估
   使用几种选定的机器学习算法来交叉验证和评估每种算法的指标。原始训练集按照50:50的比例分为训练集和验证集。
   交叉验证结果，Adaboost 算法的训练效果最好。然后使用测试数据集验证算法并评估表中的泛化效果。

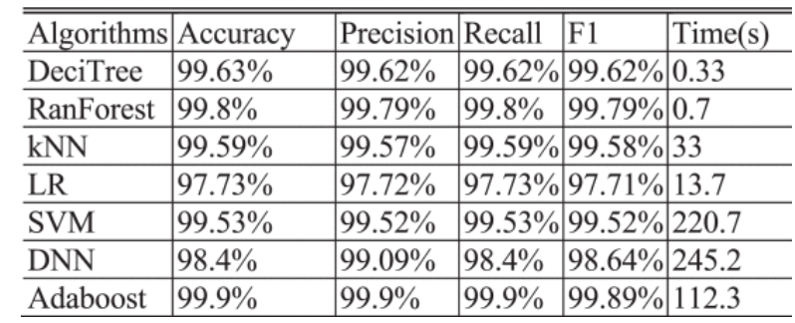
DNN整体准确率更高和决策树的运行时间更短，属于性价比最好的学习算法。

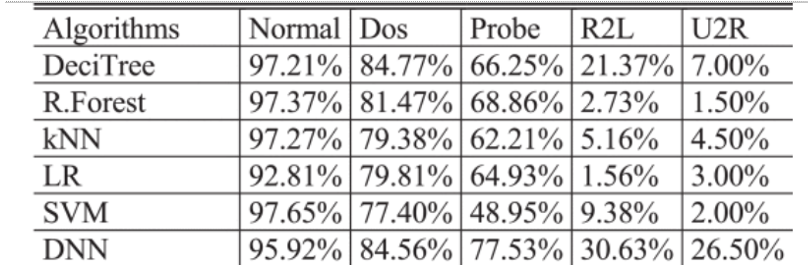
评估每种算法对不同类型数据的检测效果。

R2L和U2R数据的检测效果较差，这与之前分析的样本比例不平衡密切相关。R2L和U2R数据的检测效果较差，这与之前分析的样本比例不平衡密切相关。如果要提高整体检测效果，就必须想办法克服这些问题。虽然 DNN 的整体检测效果较好，但在 Normal 类型检测中比其他类型差。从表 7中可以看出，其他一些算法在 Normal 类型上表现良好，但在其他算法上表现不佳。因此，各种分类算法并不是对所有类型的数据都有优势，但各有优势。未来，我们将优化算法组合，利用各种算法的优势，提升整体检测效果。

使用不同数量特征的决策树的准确性

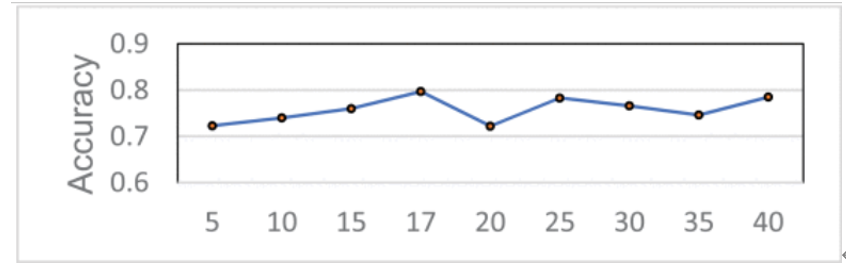
选择 Gini 最大值的特征作为划分特征。我们使用 CART (Classification and Regression Tree) 算法来测试不同数量特征的准确率。实验表明，特征的数量和选择哪些特征对检测结果的影响较大。在后续算法中，我们还将选取 17 个主要特征进行决策树的训练

3) 自适应投票结果

经过上面的测试和评估，SVM算法耗时长，精度没有优势，而Adaboost算法不理想，逻辑回归算法精度不高，放弃这三种算法。考虑到检测精度和运算性能，选择决策树、随机森林、kNN、DNN和MultiTree作为集成学习算法

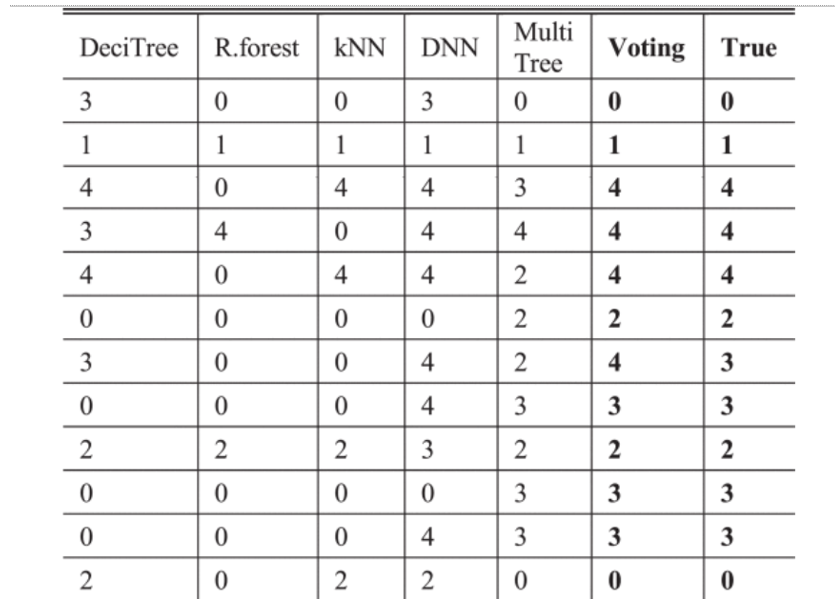
投票结果

总结：

对于不平衡的分类场景，调整样本比例、设置不同的类权重、选择合适的特征可以提高机器学习算法的准确率。在后续入侵检测领域的实际应用中，主要目标是尽可能提高训练数据的质量，优化特征提取和预处理方法，使数据更加可分离。此外，对于U2R等少数类型的攻击，应考虑单独的优化方法，以提高对此类高级威胁攻击的检测能力。

三、一种由GA和SVM组成的混合方法，用于入侵检测系统

旨在提出一种基于GA和SVM功能的异常检测技术，旨在提高入侵检测措施的有效性。

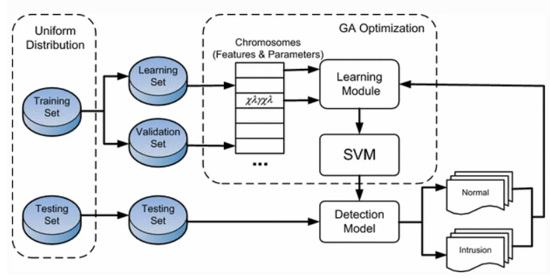
首先，GA 算法负责生成原始特征集中的特征子集。其次，使用竞争机制将具有良好分类性能的部分特征子集继承到下一代。更重要的是，通过应用交叉和变化，将生成新的特征子集，并将添加到下一代中。因此，在条件结束之前，应重复此过程并找到最佳特征子集。

GA 通常有四个组成部分。⼀个个体群体，其中每个个体都代表⼀个可能的解决⽅案。适应度函数是⼀个评估函数，我们可以通过它判断⼀个⼈是否是⼀个好的解决⽅案。⼀个选择函数，它决定如何从当前种群中挑选出优秀的个体来创造下⼀代。遗传算⼦，例如交叉和变异，它们探索搜索空间的新区域，同时保留⼀些当前信息。

提出具有非线性缩放的 SVM 模型

作为一种线性缩放方案，MinMax 归一化常用于机器学习中以预处理数据特征。然而，MinMax 归一化由于依赖于样本数据的最大值和最小值而存在局限性[6]。因此，这种缩放方式更适合数值比较集中的情况。特别是，由于 UNSW-NB15 数据集的值有很多差异，我们提出了一种独立于数据值的非线性缩放方法。根据数据分布情况，选择log函数进行预处理，描述如下
x ‾ = log ⁡ 10 { x } \overline x = \log_{10}\{x\} x=log10​{x}

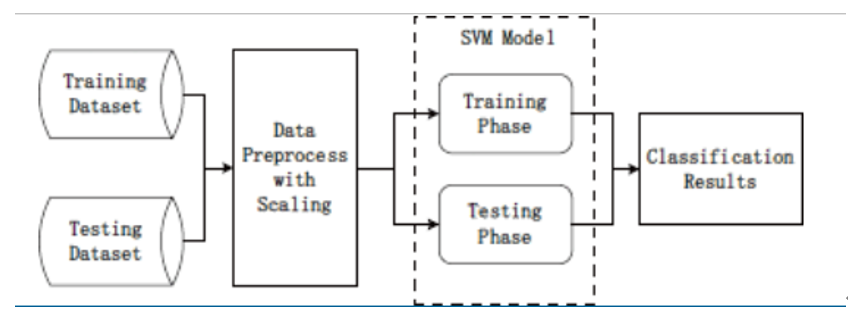
核函数用于在 SVM 模型中将低维空间映射到高维空间。常用的核函数如下：线性、多项式、径向基（RBF）、高斯、拉普拉斯、sigmoid等[7]。由于数据集很大，因此会影响训练和测试时间。综合考虑时间和精度，RBF核具有优异的综合性能，其表达式为：
$$K(x_i,x_j)=exp(\gamma |x_i-x_j{|}^2)$$

参考论文：

[1] M. Kumar, M. Hanumanthappa and T. V. S. Kumar, “Intrusion Detection System using decision tree algorithm,” 2012 IEEE 14th International Conference on Communication Technology, 2012, pp. 629-634, doi: 10.1109/ICCT.2012.6511281.

[2] Ingre, B., Yadav, A., Soni, A.K. (2018). Decision Tree Based Intrusion Detection System for NSL-KDD Dataset. In: Satapathy, S., Joshi, A. (eds) Information and Communication Technology for Intelligent Systems (ICTIS 2017) - Volume 2. ICTIS 2017. Smart Innovation, Systems and Technologies, vol 84. Springer, Cham. https://doi.org/10.1007/978-3-319-63645-0_23

[3] M. A. Jabbar and S. Samreen, “Intelligent network intrusion detection using alternating decision trees,” 2016 International Conference on Circuits, Controls, Communications and Computing (I4C), 2016, pp. 1-6, doi: 10.1109/CIMCA.2016.8053265.

[4] X. Gao, C. Shan, C. Hu, Z. Niu and Z. Liu, “An Adaptive Ensemble Machine Le arning Model for Intrusion Detection,” in IEEE Access, vol. 7, pp. 82512-82521, 2019, doi: 10.1109/ACCESS.2019.2923640.

[5] Kevric J, Jukic S, Subasi A. An effective combining classifier approach using tree algorithms for network intrusion detection[J]. Neural Computing and Applications, 2017, 28(1): 1051-1058.

[6] Mokhtar Mohammadi, Tarik A. Rashid, Sarkhel H.Taher Karim, Adil Hussain Mohammed Aldalwie, Quan Thanh Tho, Moazam Bidaki, Amir Masoud Rahmani, Mehdi Hosseinzadeh,

A comprehensive survey and taxonomy of the SVM-based intrusion detection systems,Journal of Network and Computer Applications,Volume 178,2021,102983,ISSN 1084-8045,https://doi.org/10.1016/j.jnca.2021.102983.(https://www.sciencedirect.com/science/article/pii/S1084804521000102)

[7] S. Teng, N. Wu, H. Zhu, L. Teng and W. Zhang, “SVM-DT-based adaptive and collaborative intrusion detection,” in IEEE/CAA Journal of Automatica Sinica, vol. 5, no. 1, pp. 108-118, Jan. 2018, doi: 10.1109/JAS.2017.7510730.

–end–