题目
首先先来看题目描述:
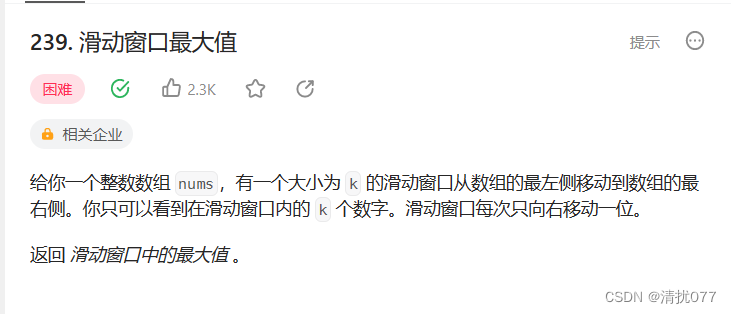
这是一道栈与队列相关的题,给定我们一个整型数组,有一个长度为k的滑动窗口,让我们计算每次窗口的最大值。
我们的想法可以是得到一队列数据结构,让进入这个队列的第一个数据一定是最大的,而进入这个队列之后的数据在内部进行操作,每次移动数据一进一出,但是不影响我们的前提,就是第一个数据为队列的最大值,也就是滑动窗口的最大值。
思路分析
所以我们考虑实现下边的队列:
class myQueue
{
public:
//确保为单调队列,所以小于插入的数时,都进行删除,之后再插入
void push(int x)
{}
//确保第一个数一定为最大值
void pop(int x)
{}
int max()
{}
private:
};
在知道这个队列的大体结构之后,我们来实现这个队列的细节。
首先我要选择什么容器来实现这个队列呢?
vector可以吗?list可以吗?都可以,但是有观察过stl源码的同学都知道,stl的queue底层都是通过双端队列deque来实现的,他是一种特殊的数据结构,是一种双开口的"连续"空间的数据结构,双开口的含义是:可以在头尾两端进行插入和删除操作,且时间复杂度为O(1),与vector比较,头插效率高,不需要搬移元素;与list比较,空间利用率比较高。
在确定好什么容器来实现之后,我们来考虑pop,push应该如何实现。
pop很简单,我们要移除前边的数据时,我们来判断单调队列的队头与该数据是否相等,相等就说明该数据是上个滑动窗口的最大值,如果不相等,那么说明这个数据并没有在单调队列中,那么就不进行处理。
push呢?其实就是将一个数据从队尾开始比较,如果比队尾的数据大,那么就将队尾数据出队,当队列数据都比这个数大时,再进行入队,还是要确保这个队列是一个单调队列,并且队列第一个数据为最大值。
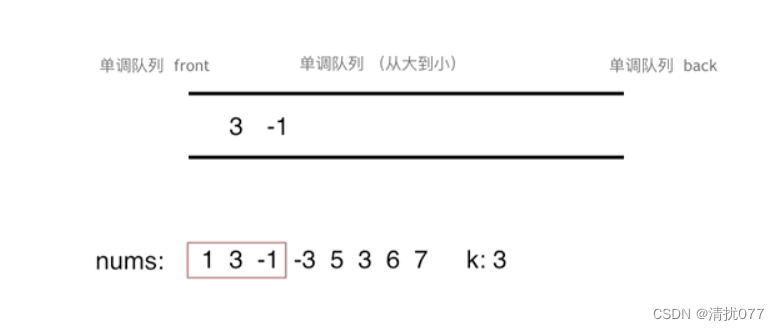
所以单调队列的代码可以这样实现:
class myQueue
{
public:
//确保为单调队列,所以小于插入的数时,都进行删除,之后再插入
void push(int x)
{
while(!dq.empty() && x > dq.back())
{
dq.pop_back();
}
dq.push_back(x);
}
//确保第一个数一定为最大值
void pop(int x)
{
if(!dq.empty() && x==dq.front())
{
dq.pop_front();
}
}
int max()
{
return dq.front();
}
private:
deque<int> dq;
};
代码实现
当实现好单调队列的代码之后,我们在主函数中只需要控制每次窗口滑动,一进一出就好了。
并且使用一个vector容器来保存每次队列的max最大值。
class myQueue
{
public:
//确保为单调队列,所以小于插入的数时,都进行删除,之后再插入
void push(int x)
{
while(!dq.empty() && x > dq.back())
{
dq.pop_back();
}
dq.push_back(x);
}
//确保第一个数一定为最大值
void pop(int x)
{
if(!dq.empty() && x==dq.front())
{
dq.pop_front();
}
}
int max()
{
return dq.front();
}
private:
deque<int> dq;
};
class Solution {
public:
vector<int> maxSlidingWindow(vector<int>& nums, int k) {
vector<int> ret;
myQueue mq;
for(int i=0;i<k;i++)
{
mq.push(nums[i]);
}
ret.push_back(mq.max());
for(int i = k;i<nums.size();i++)
{
mq.pop(nums[i-k]);
mq.push(nums[i]);
ret.push_back(mq.max());
}
return ret;
}
};