目录
💥1 概述
📚2 运行结果
🎉3 参考文献
👨💻4 Matlab代码
💥1 概述
本文提出了一种用于反狙击应用的源定位过程:使用广义互相关(GCC)方法确定到达时间差(TDOA)值。时差值由混合球面插值/最大似然(SI/ML)估计方法用于确定射手位置。
📚2 运行结果
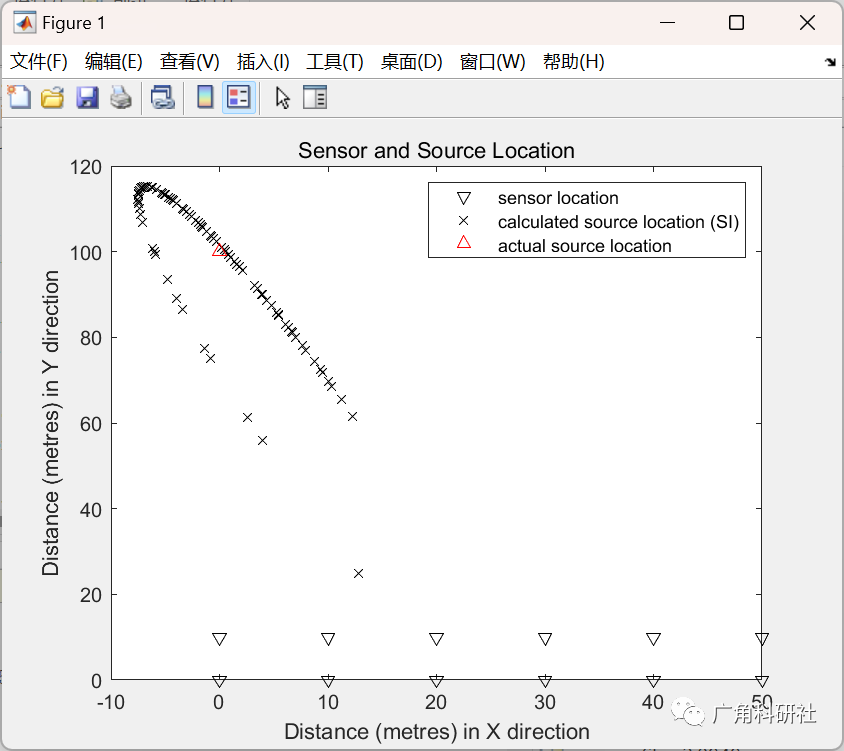
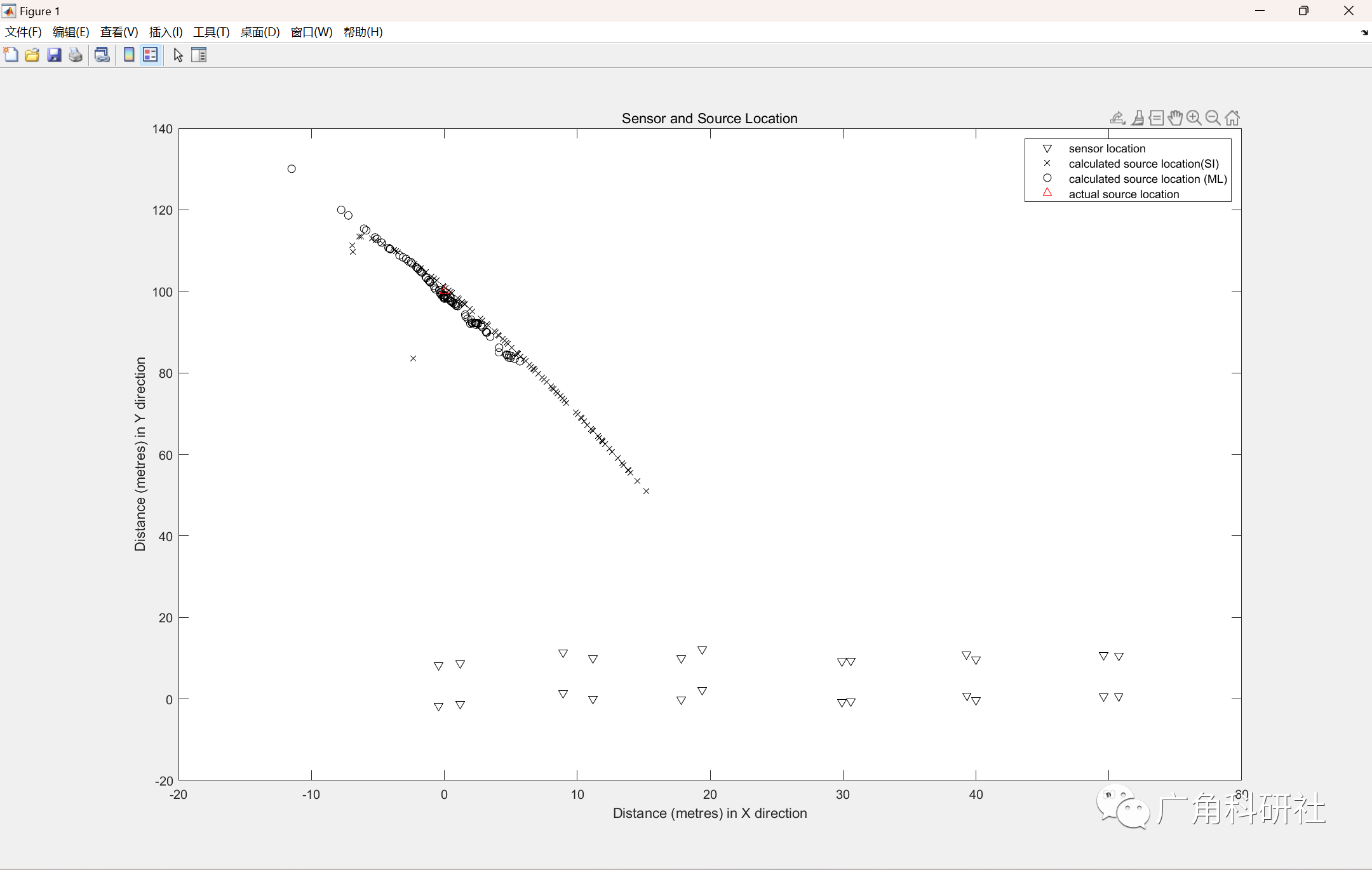
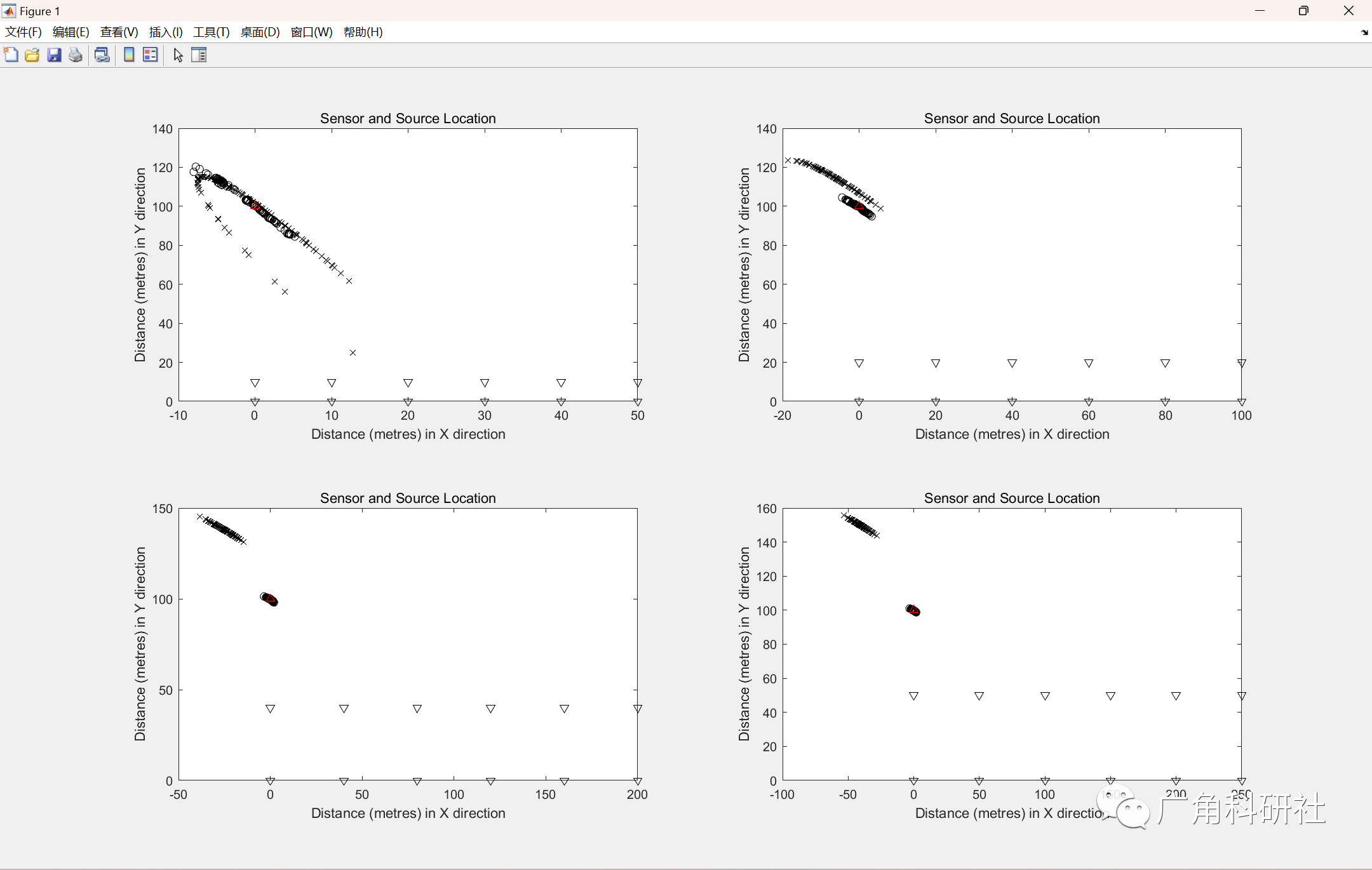
主函数部分代码:
clc;
close all;
clear all;% N sensors, 1 source. Using sensor 1 as reference i.e (x1=0, y1=0, z1=0)
% -----------------------------------------------------
% Definition
% -----------------------------------------------------
nRun=100; % number of Monte Carlo runs
% uncomment one of them
bML=0; % turn off ML calculation
%bML=1; % turn on ML calculation
% uncomment one of them
perturb=0; % turn off location perturbation
% perturb=1; % turn on location perturbation
% ----------------------------------------------------------------
% Actual source location (m) in Cartesian coordinates x, y and z
% Note: For simplicity, we only varies y for our simulation
% ----------------------------------------------------------------
xs_src_actual=[0];
% Varies the Y position (Choose 1)
%------------------------------------
ys_src_actual=[100]; %100 m
zs_src_actual=[0];
Rs_actual=sqrt(xs_src_actual.^2 + ys_src_actual.^2 + zs_src_actual.^2);
% calculate corresponding range Rs
bearing_actual=[xs_src_actual; ys_src_actual; zs_src_actual]/Rs_actual;
% calculate corresponding bearing
% ----------------------------------------------------------------
% Actual sensor location (m) in Cartesian coordinates x, y and z
% Note: For simplicity, we only use integers and then multiply with
% a scaling factor to produce the actual coordinates.
% e.g. [5 10 15] = [1 2 3] * 5 ;
% ----------------------------------------------------------------
% Scale wrt to 1m (Choose 1)
%------------------------------
scale_dist = 10; % 10 m
% (Choose 1 of the following sensor configuration for study)
%-------------------------------------------------------------
% 12x2 sensors arranged 2 rows
xi=[0 0 1 1 2 2 3 3 4 4 5 5 0 0 1 1 2 2 3 3 4 4 5 5 ].*scale_dist;
yi=[0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1].*scale_dist;
zi=[0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1].*1.0;
%20x2 sensors arranged 2 rows
% xi=[0 0 1 1 2 2 3 3 4 4 5 5 6 6 7 7 8 8 9 9 0 0 1 1 2 2 3 3 4 4 5 5 6 6 7 7 8 8 9 9].*scale_dist;
% yi=[0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1].*scale_dist;
% zi=[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1].*1.0;
% % Soldier configuration (each with 2 sensors). z= 1m apart vertically
temp=size(xi);
nSen=temp(1,2); % number of sensor (>4)
noisestd=1;
if (perturb==1)
randn('state',0);
tmp1=randn(3, nSen);
for i=1:2:nSen
xi(i)= xi(i) + noisestd*tmp1(1,i);
xi(i+1)= xi(i+1)+(noisestd+0.01)*tmp1(1,i); % less variance on the body
yi(i)= yi(i) + noisestd*tmp1(2,i);
yi(i+1)= yi(i+1)+(noisestd+0.01)*tmp1(2,i); % less variance on the body
end
zi=zi+0.01*tmp1(3,:); % less variance on the body
end
% RD noise (Choose 1)
% -----------------------------------------------------
Noise_Factor=0.02;
% noise std = Std_Norm * (source distance). %we expect bigger noise variance for larger distance.
Noise_Var=(Noise_Factor*Rs_actual)^2;
% -----------------------------------------------------
% Functions
% -----------------------------------------------------
% Random Process
% AWGN
randn('state',0);
noise = sqrt(Noise_Var)*randn(nRun, 1);
%noise_mean = mean(noise, 2); % average along row
for k=1:nRun % Monte Carlo Simulation
Xi=[xi' yi' zi'];
Di= sqrt ((xi-xs_src_actual).^2 + (yi-ys_src_actual).^2 + (zi-zs_src_actual).^2);%distance between source ans sensor i
Ri= sqrt ((xi).^2 + (yi).^2 + (zi).^2);%distance between origin and sensor i
locSen=[xi' yi' zi'];
% using N sensors
for i=1:nSen-1
%d21=Di(2)-Di(1);
%d31=Di(3)-Di(1);..
%dn1=Di(n)-Di(1);
%d=[d21;d31;...;dn1];
d(i,1)=Di(i+1)-Di(1)+noise(k); %add noise to RD estimates%distance between sensor i,1
% delta2=Ri(2)^2-d(1)^2;
% delta3=Ri(3)^2-d(1)^2;...
% deltan=Ri(n)^2-d(1)^2;
% delta=[delta2;delta3;...deltan];
delta(i,1)=Ri(i+1)^2-d(1)^2;%delta
% s2= [xi(2) yi(2) zi(2)];
% s3= [xi(3) yi(3) zi(3)];...
% sn= [xi(n) yi(n) zi(n)];
% s=[s2;s3;...sn];
s(i,:)=[xi(i+1) yi(i+1) zi(i+1)];
end
🎉3 参考文献
[1]高强. 基于传感器网络的室内人员定位算法研究[D].东北大学,2011.
部分理论引用网络文献,若有侵权联系博主删除。