一些口诀

长杠变短杠，开口换方向

其实意思是底下这个

$$\overline{C\cap D}=\overline{C}\cup \overline{D}$$

---

可导必可微，可微必可导

二者互为充要条件

---

可导必定连续，连续未必可导。连续必定可积,可微未必可积

题外话，连续必有极限。

再题外话，摘抄网上的42条口诀，鉴于网上互相抄且不注明出处，此处也无法考究其真正出处：

1. 函数概念五要素，定义关系最核心。
2. 分段函数分段点，左右运算要先行。
3. 变限积分是函数，遇到之后先求导。
4. 奇偶函数常遇到，对称性质不可忘。
5. 单调增加与减少，先算导数正与负。
6. 正反函数连续用，最后只留原变量。
7. 一步不行接力棒，最终处理见分晓。
8. 极限为零无穷小，乘有限仍无穷小。
9. 幂指函数最复杂，指数对数一起上。
10. 待定极限七类型，分层处理洛必达。
11. 数列极限洛必达，必须转化连续型。
12. 数列极限逢绝境，转化积分见光明。
13. 无穷大比无穷大，最高阶项除上下。
14. n项相加先合并，不行估计上下界。
15. 变量替换第一宝，由繁化简常找它。
16. 递推数列求极限，单调有界要先证，两边极限一起上，方程之中把值找。
17. 函数为零要论证，介值定理定乾坤。
18. 切线斜率是导数，法线斜率负倒数。
19. 可导可微互等价，它们都比连续强。
20. 有理函数要运算，最简分式要先行。
21. 高次三角要运算，降次处理先开路。
22. 导数为零欲论证，罗尔定理负重任。
23. 函数之差化导数，拉氏定理显神通。
24. 导数函数合(组合)为零，辅助函数用罗尔。
25. 寻找ξ η无约束，柯西拉氏先后上。
26. 寻找ξ η有约束，两个区间用拉氏。
27. 端点、驻点、非导点，函数值中定最值。
28. 凸凹切线在上下，凸凹转化在拐点。
29. 数字不等式难证，函数不等式先行。
30. 第一换元经常用，微分公式要背透。
31. 第二换元去根号，规范模式可依靠。
32. 分部积分难变易，弄清u、v是关键。
33. 变限积分双变量，先求偏导后求导。
34. 定积分化重积分，广阔天地有作为。
35. 微分方程要规范，变换，求导，函数反。
36. 多元复合求偏导，锁链公式不可忘。
37. 多元隐函求偏导，交叉偏导加负号。
38. 多重积分的计算，累次积分是关键。
39. 交换积分的顺序，先要化为重积分。
40. 无穷级数不神秘，部分和后求极限。
41. 正项级数判别法，比较、比值和根值。
42. 幂级数求和有招，公式、等比、列方程。

---

函数求导

求导法则

有点像高中知识，看来我是都忘了

$$(f(x)\pm g(x){)}^{\prime }=f^{\prime }(x)\pm g^{\prime }(x)$$
$$(f(x)\cdot g(x){)}^{\prime }=f^{\prime }(x)\cdot g(x)+f(x)\cdot g^{\prime }(x)$$
$$(\frac{f(x)}{g(x)}{)}^{\prime }=\frac{f^{\prime }(x)\cdot g(x)-f(x)\cdot g^{\prime }(x)}{g^2(x)}$$
$$(\frac{1}{f(x)}{)}^{\prime }=\frac{-f^{\prime }(x)}{f^2(x)}$$

驻点

驻点是函数一阶导数为0的点

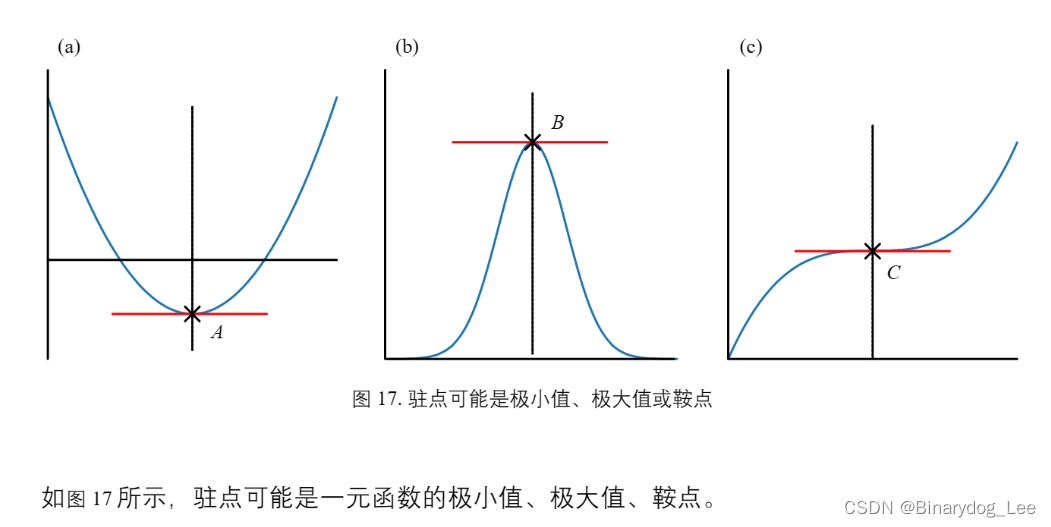
（图引自《数学要素》 | 鸢尾花书）

求极限

求极限可能用到的方法（可能综合使用）

1. 从基础定义入手（按照${\lim }_{\Delta x\to ?}\frac{f(x+\Delta x)-f(x)}{\Delta x}$化简）
2. 从几何关系分析（基础的$x^2$那种的推导）
3. 洛必达（特定情况适用）
4. 夹逼定理（一般还是要放缩出两边才能夹住）
5. 放缩（利用不等式）

$dx$是$\Delta x$趋向于0的精确值（$\Delta$是近似值，$d$是精确值）

可导必连续，连续未必可导

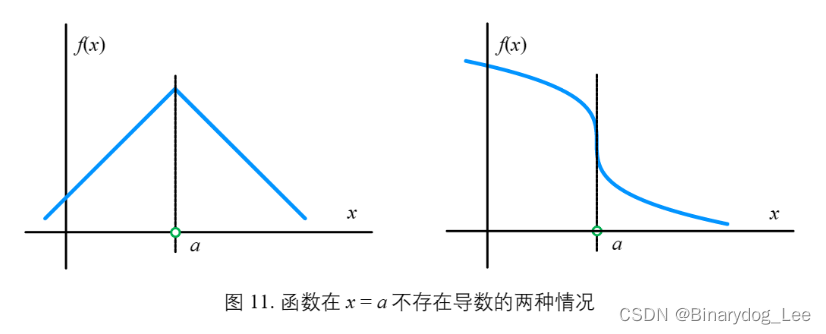
（图引自《数学要素》 | 鸢尾花书）

函数图形

极值

一阶可导点是极值的必要条件（费马定理）

判断极值的第二充分条件$f(x)$驻点处看$f^{\prime \prime }(x)$，若$f^{\prime \prime }(x)>0$是极小值，若$f^{\prime \prime }(x)<0$是极大值

---

意思是若依照驻点找极值点，应当看二阶导判断驻点是哪种极值点

隐函数求极值

先按隐函数求导求出一阶导数，一阶导数中代入$y^{\prime }=0$，得到一个$y=f(x)$的关系式，该关系式代回原隐函数可以得到一个点，是驻点，接着使用一阶导数求二阶导数，根据二阶导数的正负判断是哪种极值（极大值/极小值）

凸凹性

弧在弦下为凹，弧在弦上为凸。凸凹性的判断看二阶导的正负，正凹负凸

拐点

二阶可导点是拐点的必要条件（二阶导某点左右异号即为拐点）

拐点是凹弧与凸弧的分界，该点是否可导与是不是拐点无必然联系。找的点可以是未定义的点（如分母不能为零），也可以是二阶导为0的点。因为判断的根本条件是两侧是否异号，找到之后也要验证一下（有时候未必异号）。

作函数图像

若有渐近线应当画出来。

曲率

分为两种情况，即常规方程和参数方程。

$$K=\frac{|y^{\prime \prime }|}{(1+y^{\prime 2}{)}^{\frac{3}{2}}}$$

$$K=\frac{|x_t^{\prime }{y}_t^{\prime \prime }-x_t^{\prime \prime }{y}_t^{\prime }|}{(x_t^{\prime 2}+y_t^{\prime 2}{)}^{\frac{3}{2}}}$$

幂指函数

幂指函数是初等函数，主要记住公式：

$$u^v=e^{v\ln u}$$
$$u(x{)}^{v(x)}=e^{v(x)\ln u(x)}$$
$$x^x=e^{x\ln x}$$

---

例题：画出$x>0$时函数$x^x$的大致图像

①看定义域左右极限：根据$x\in (,+\infty )$：

$$\underset{x\to 0^{+}}{\lim }{x}^x=e^{{\lim }_{x\to 0^{+}}x\ln x}=e^0=1$$

$$\underset{x\to +\infty }{\lim }{x}^x=+\infty$$

②求导看单调性：

$$(x^x{)}^{\prime }=(e^{x\ln x}{)}^{\prime }=(e^{x\ln x})(x\ln x{)}^{\prime }=x^x(\ln x+1)$$

发现$x=\frac{1}{e}$是导数0点，易发现$(0,\frac{1}{e})$导数小于0，单调递减，右侧$(\frac{1}{e},+\infty )$导数大于0，单调递增。

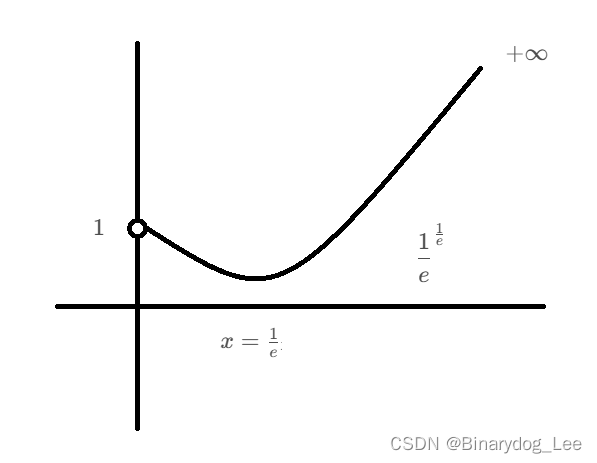
附：$$\underset{x\to 0^{+}}{\lim }x\ln x=\underset{x\to 0^{+}}{\lim }\frac{\ln x}{1/x}$$

按洛必达法则可求出极限为0