标准CSO

Cheng R, Jin Y. A competitive swarm optimizer for large scale optimization[J]. IEEE transactions on cybernetics, 2014, 45(2): 191-204.

1.1 背景介绍

CSO（competitive swarm optimizer）算法是在PSO（particle swarm optimization）算法的基础上改进而来的。PSO算法是一种功能强大、应用广泛的群体智能算法，主要用来解决优化问题。PSO算法包含一个粒子群，粒子群里面的每个粒子均有1个 $n$ 维位置变量和1个 $n$ 维速度变量。在算法的每次迭代过程中，每个粒子的位置变量 $X_{i}$ 和速度变量 $V_{i}$ 通过以下公式进行更新：

$\begin{aligned} V_{i}(t+1)=\omega V_{i}(t) & +c_{1}R_{1}(t)(pbest_{i}(t)-X_{i}(t)) +c_{2} R_{2}(t)(gbest(t)-X_{i}(t)) \end{aligned}$

$X_{i}(t+1)=X_{i}(t)+V_{i}(t+1)$

其中 $t$ 是当前迭代数， $\omega$ 是惯性权重， $c_{1}$ 和 $c_{2}$ 是加速度系数， $R_{1}(t)$ 和 $R_{2}(t)$ 是两个向量，向量中每个元素取值范围为 $0,1]^{n}$ ， $pbest_{i}(t)$ 是第 $i$ 个粒子的历史最优解， $g b es t (t)$ 是所有粒子的历史最优解。 $c_{1}R_{1}(t)(pbest_{i}(t)-X_{i}(t))$ 为认知部分， $c_{2} R_{2}(t)(gbest(t)-X_{i}(t))$ 为社会部分。

当优化问题存在大量局部最优值和具有高维特点时，传统PSO算法在处理此类问题时会过早收敛，从而导致其优化效果不佳。首先来看 $g b es t$ 对算法收敛过程的影响，将上述公式进行变换，可得：

$V_{i}(t+1)=\omega V_{i}(t)+\theta_{1}(p_{1}-X_{i}(t))$

其中，

$\theta_{1}=c_{1}R_{1}(t)+c_{2} R_{2}(t)$

$p_{1} =\frac{c_{1} R_{1}(t)}{c_{1} R_{1}(t)+c_{2} R_{2}(t)} pbest_{i}(t) +\frac{c_{2} R_{2}(t)}{c_{1} R_{1}(t)+c_{2} R_{2}(t)}gbest(t)$

$p_{1}$ 和 $X_{i}$ 的差决定了粒子群的种群多样性，而 $pbest_{i}$ 和 $g b es t$ 的取值多样性决定了 $p_{1}$ 取值的多样性。由于 $g b es t$ 的影响，随着迭代过程的继续，粒子逐渐向 $g b es t$ 靠拢，这导致 $pbest_{i}$ 逐渐接近 $g b es t$ ，进而导致粒子群的种群多样性大幅降低。 $p_{1}$ 在很大程度上决定着传统PSO算法在搜索过程中的勘探能力和开采能力。

为了解决传统PSO算法的过早收敛问题，本文提出了CSO算法。该算法去掉了 $pbest_{i}$ 和 $g b es t$ 两个变量，引入了粒子间的成对竞争机制。在该机制中，竞争失败的粒子将向竞争胜利的粒子学习，而不是向 $pbest_{i}$ 和 $g b es t$ 学习，这将较好地解决传统PSO算法的过早收敛问题。

1.2 算法流程

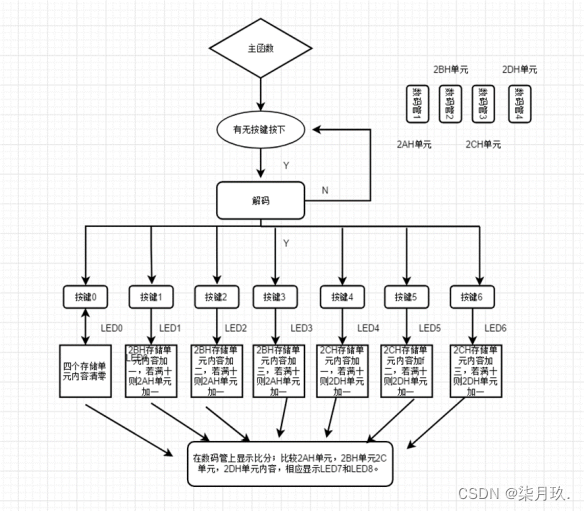
CSO算法的总体思想如图所示。在每一次迭代过程中，随机从粒子群 $P (t)$ 中选择一对粒子进行竞争。竞争成功的粒子直接进入下一次迭代，竞争失败的粒子将向竞争成功的粒子学习并更新自己的位置变量和速度变量。该操作完成后，将这一对粒子从粒子群 $P (t)$ 中剔除，将竞争成功的粒子和更新后的失败粒子加入到粒子群 $P (t + 1)$ 中。当所有粒子从粒子群 $P (t)$ 中移到粒子群 $P (t + 1)$ 中后，算法进入下一次迭代。根据上图可知，每一次迭代将会使粒子群 $P$ 中一半的粒子得到更新。

竞争失败的粒子的速度变量和位置变量更新如以下公式所示：

$\begin{aligned} V_{l, k}(t+1) & =R_{1}(k, t) V_{l, k}(t) +R_{2}(k, t)(X_{w, k}(t)-X_{l, k}(t)) +\varphi R_{3}(k, t)(\bar{X}_{k}(t)-X_{l, k}(t)) \end{aligned}$

$X_{l, k}(t+1) = X_{l, k}(t)+V_{l, k}(t+1)$

其中， $X_{w, k}(t)$ 表示第 $t$ 代的第 $k$ 轮竞争中竞争成功粒子的位置， $X_{l, k}(t)$ 表示第 $t$ 代的第 $k$ 轮竞争中竞争失败粒子的位置， $V_{l, k}(t)$ 表示第 $t$ 代的第 $k$ 轮竞争中竞争失败粒子的速度， $R_{1}(k, t)$ 、 $R_{2}(k, t)$ 、 $R_{3}(k, t) \in \left [ 0,1 \right ]$ 分别表示算法第 $t$ 次迭代的第 $k$ 轮竞争中随机生成的向量。

$\bar{X}_{k}(t)$ 表示第 $t$ 代的第 $k$ 轮竞争中相关粒子的位置平均值，它分为全局版本和局部版本。

$\bar{X}_{k}^{g}(t)$ 表示 $P (t)$ 中所有粒子的位置平均值，是全局版本。
$\bar{X}_{l,k}^{l}(t)$ 表示在竞争失败粒子的预定义邻域内所有粒子的位置平均值，是局部版本。领域控制可以增加粒子群的种群多样性，这可能会提高CSO算法的搜索能力。

function [best_x, best_y, best_y_history] = Optimizer_CSO(obj_fun, num_vari, lower_bound, upper_bound, pop_size, max_gen, varphi)
generation = 1;
best_y_history = [];
pop_size = pop_size - rem(pop_size, 2);  % rem：除后的余数。保证种群数是偶数。
pop_position = lhsdesign(pop_size, num_vari) * (upper_bound - lower_bound) + lower_bound;    % 初始化种群
pop_fitness = feval(obj_fun, pop_position);  % 计算种群的适应度函数值
pop_velocity = zeros(pop_size, num_vari);
while generation < max_gen - 1  % 迭代求解，保证总的评估次数为0.5*pop_size*max_gen
    randrows = randperm(pop_size);  % 模拟随机选择两个粒子的过程
    mean_pop_position = mean(pop_position);     % 这一行代码也可以放在for循环中
    for i = 1 : pop_size / 2
        first_particle = randrows(2 * (i - 1) + 1);
        second_particle = randrows(2 * i);
        if pop_fitness(first_particle) <=  pop_fitness(second_particle)   % 这里以求目标函数最小值为例
            win = first_particle;
            loss = second_particle;
        else
            win = second_particle;
            loss = first_particle;
        end
        pop_velocity(loss, :) = rand(1, num_vari) .* pop_velocity(loss, :) + ...    % 更新失败的粒子
            rand(1, num_vari) .* (pop_position(win, :) - pop_position(loss, :)) + ...
            varphi * rand(1, num_vari) .* (mean_pop_position - pop_position(loss, :));
        position = pop_position(loss, :) + pop_velocity(loss, :);
        position(position > upper_bound) = upper_bound;
        position(position < lower_bound) = lower_bound;     % 越界检查
        pop_position(loss, :) = position;
        pop_fitness(loss) = feval(obj_fun,pop_position(loss, :));
    end
    [best_y, ind] = min(pop_fitness);
    best_x = pop_position(ind, :);
    best_y_history = [best_y_history; best_y];
    %fprintf("CSO generation: %d fmin: %.4f\n", generation, best_y);
    generation = generation + 1;
end
end

$R_{1}(k, t) V_{l, k}(t)$ 类似传统PSO算法中的惯性项，用来保证CSO算法搜索的稳定性； $R_{2}(k, t)(X_{w, k}(t)-X_{l, k}(t))$ 是CSO算法的认知部分； $\varphi R_{3}(k, t)(\bar{X}_{k}(t)-X_{l, k}(t))$ 是CSO算法的社会部分。

CSO算法流程如1.1所示。算法的时间复杂度为 $\times m \times n)$ 。 $t < ma x T - 1$ 的目的是保证样本总的评估次数维持在 $0.5\times maxT \times m$ 次；随机排序的目的是模拟每次随机取两个粒子。

1.3 勘探能力与开采能力分析

首先分析一下CSO算法的勘探能力，我们将上述公式转换：

$V_{i}(t+1)=R_{1}(k, t)V_{i}(t)+\theta_{2}(p_{2}-X_{i}(t))$

$\begin{aligned} \theta_{2} &=R_{2}(k, t)+ \varphi R_{3}(k, t)\\ p_{2} &=\frac{R_{2}(k, t)}{R_{2}(k, t)+\varphi R_{3}(k, t)} X_{w}(t)+\frac{\varphi R_{3}(k, t)}{R_{2}(t)+\varphi R_{3}(k, t)} \bar{X}(t) \end{aligned}$

CSO算法的种群多样性是高于传统PSO算法的，因为 $X_{w}(t)$ 和 $\bar{X}(t)$ 的取值更加地多样。下面展示CSO算法的勘探能力是如何高于传统PSO算法的。

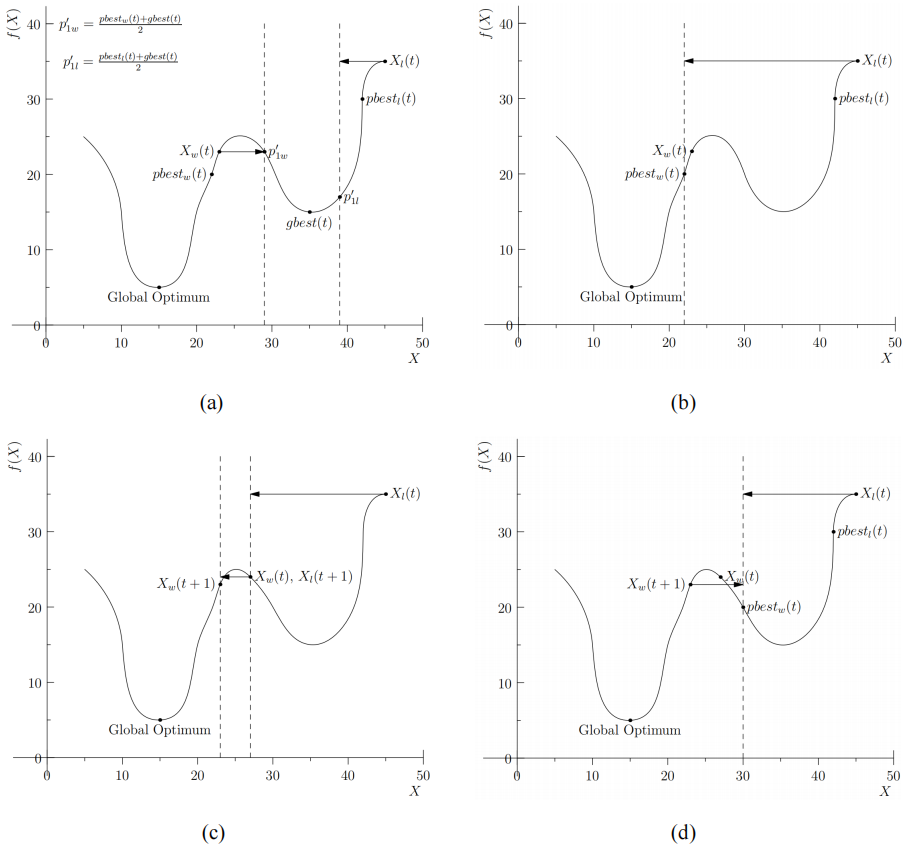
首先看图a， $g b es t (t)$ 陷入了局部最优，在传统PSO算法中，两个被选择的粒子均会向 $g b es t (t)$ 靠近，这最终使得算法陷入局部最优的陷阱，导致算法优化结果的不佳。现在去掉向 $g b es t (t)$ 更新的方式，所有粒子均只向各自的 $p b es t (t)$ 更新，如图b。从图可以看出，被选择的粒子会跳出局部最优的陷阱，使得算法的勘探能力得到了提升。但是如果 $p b es t (t)$ 也陷入了局部最优，如图c，算法也会陷入局部最优的陷阱，导致算法的勘探能力下降。因此，去掉向 $g p b es t (t)$ 更新的方式，粒子的更新采用成对粒子竞争更新机制，传统PSO算法也就演变为CSO算法。如图d，由于所有粒子分布在样本空间的不同位置，粒子的更新就变得更加多样化，非常有助于算法脱离局部最优的陷阱，从而使得算法的勘探能力大幅提升。

然后分析一下CSO算法的开采能力。CSO算法的开采阶段是在勘探阶段之后，是在勘探阶段基础上继续小规模地提高算法的优化结果。在传统的PSO算法中，有以下关系：

$\left\{\begin{array}{l} f(gbest(t)) \leq f\left(pbest_{w}(t)\right) \leq f\left(X_{w}(t)\right) \\ f(gbest(t)) \leq f\left(best_{l}(t)\right) \leq f\left(X_{l}(t)\right) \end{array}\right.$

随着迭代过程的继续， $t$ 越来越大，有：

$\left\{\begin{array}{l} pbest_{w}(t) \approx gbest(t) \\ pbest_{l}(t) \approx gbest(t) \end{array}\right.$

然后令：

$\begin{aligned} \Delta F_{1}(t) & =\mid f\left(X_{l}(t)\right)-f(gbest) \mid \\ & =\left|f\left(X_{l}(t)\right)-f\left(\frac{gbest(t)+gbest(t)}{2}\right)\right| \\ & \approx\left|f\left(X_{l}(t)\right)-f\left(\frac{gbest(t)+pest_{l}(t)}{2}\right)\right| \\ & =\left|f\left(X_{l}(t)\right)-f\left(p_{1}^{\prime}\right)\right| \\ \Delta F_{2}(t) & =\left|f\left(X_{l}(t)\right)-f\left(X_{w}(t)\right)\right| \\ & =\left|f\left(X_{l}(t)\right)-f\left(p_{2}^{\prime}\right)\right| \end{aligned}$

其中 $p_{1}^{\prime}$ 是 $p_{1}$ 的数学期望， $p_{2}^{\prime}$ 是 $p_{2}$ 在 $\varphi = 0$ 的数学期望。可以得到：

$\Delta F_{2}(t)\leq \Delta F_{1}(t)$

与传统PSO算法相比，CSO算法有更好的能力开发与最优粒子相接近的粒子，也就是其开发能力更好，即局部搜索能力更强。此证明过程主要与其勘探过程结合来看。

1.4 算法收敛证明

首先重写之前的公式：

$\begin{aligned} V_{i}(t+1) & =\frac{1}{2} V_{i}(t) +\frac{1}{2}(X_{w}(t)-X_{i}(t)) +\varphi \frac{1}{2}(\bar{X}_{i}(t)-X_{i}(t)) \\ X_{i}(t+1) &= X_{i}(t)+V_{i}(t+1) \end{aligned}$

定理一：给定任何 $\varphi \ge 0$ ，上述公式可以收敛。

下面来证明这个定理。首先将上述公式进行转换：

$\begin{aligned} V_{i}(t+1)&=\frac{1}{2} V_{i}(t)+\theta\left(p-X_{i}(t)\right) \\ X_{i}(t+1)&=X_{i}(t)+V_{i}(t+1)\\ \theta&=\frac{1+\varphi}{2} \\ p&=\frac{1}{1+\varphi} X_{w}(t)+\frac{\varphi}{1+\varphi} \bar{X}(t) \end{aligned}$

将上面两个公式转换为矩阵形式，可得：

$y (t + 1) = A y (t) + Bp$

其中，

$y(t)=\left[\begin{array}{l} V_{i}(t) \\ X(t) \end{array}\right], A=\left[\begin{array}{cc} \frac{1}{2} & -\theta \\ \frac{1}{2} & 1-\theta \end{array}\right], B=\left[\begin{array}{l} \theta \\ \theta \end{array}\right]$

其中，在动力系统理论中， $A$ 称作状态矩阵， $p$ 称作外部输入， $B$ 称作输入矩阵。如果根据动力系统理论，上述公式能否收敛取决于状态矩阵 $A$ 的特征值。首先来求解状态矩阵 $A$ 的特征值：

$\lambda^{2}-\left(\frac{3}{2}-\theta\right) \lambda+\frac{1}{2}=0$

其特征值为：

$\left\{\begin{array}{l} \lambda_{1}=\frac{3}{4}-\frac{\theta}{2}+\frac{\sqrt{\left(\frac{3}{2}-\theta\right)^{2}-2}}{2} \\ \lambda_{2}=\frac{3}{4}-\frac{\theta}{2}-\frac{\sqrt{\left(\frac{3}{2}-\theta\right)^{2}-2}}{2} \end{array}\right.$

上述公式收敛的充分必要条件为 $\left | \lambda _{1} \right | < 1$ 和 $\left | \lambda _{2} \right | < 1$ 。因此，可以得到：

$\theta > 0$

将 $\theta$ 转换为 $\varphi$ ：

$\varphi > -1$

所以，给定任何 $\varphi \ge 0$ ，CSO算法可以收敛。

1.5 实验研究

首先来看一下不同种群大小下CSO算法的优化结果，优化结果见表1.1。算法实验的测试函数集为CEC2008，测试函数的维度统一设置为200， $\varphi$ 设置为0，实验的测试函数为 $f_{1}$ 、 $f_{2}$ 、 $f_{3}$ 和 $f_{6}$ ，实验的种群数分别为20、40、80、100、 200、400和800，实验总的评估次数为5000 $\times$ n，算法运行10次，取10次结果的平均值作为算法最终的优化结果。根据表1.1可以看出，种群数量过大或者过小对CSO算法的优化都有不利的影响。当种群数量过大时，种群收敛速度比较慢，而且算法的迭代次数会减少，导致其优化结果不佳；当种群数量过少时，虽然算法的迭代次数会增加，但种群其收敛速度过快，从而导致算法过早收敛，这也会造成其优化结果不佳。