电脑提示msvcr120.dll丢失是一个常见的问题，这个问题通常会在你尝试打开某些程序或游戏时出现。这个问题的原因是因为你的电脑缺少了一个名为msvcr120.dll的文件，这个文件是微软Visual C++ Redistrle for Visualv 2013的一部分。如果你遇到了这个问题，不要担心，下面是三种解决方法：

解决方法一

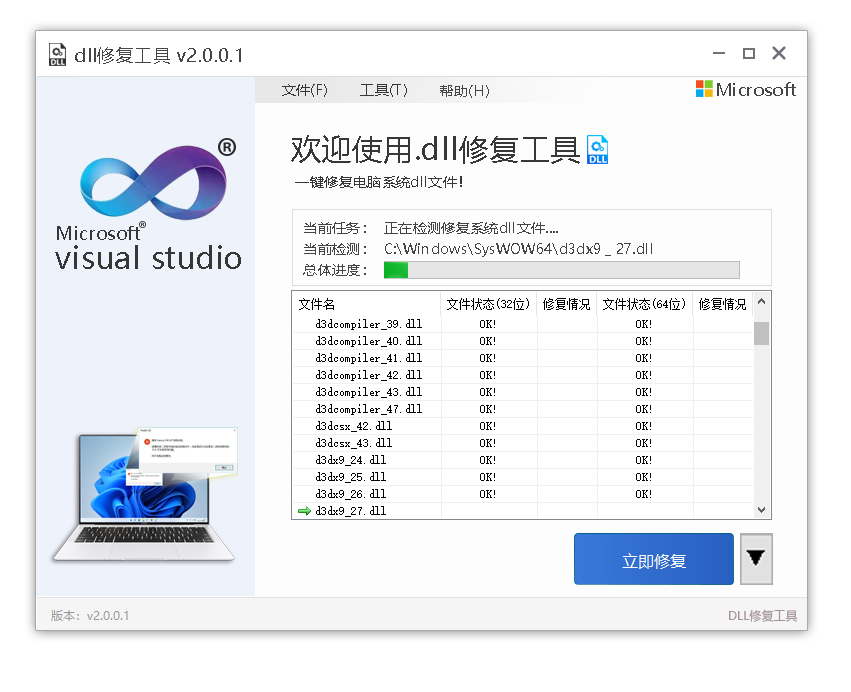
1、直接使用dll修复程序进行修复，可以一键自动检测你系统到底缺失了哪些dll文件，然后再帮你安装修复完成。

2、dll修复程序-一键自动修复电脑msvcr120.dll丢失的问题

3、可以到电脑浏览器顶部网页栏目搜索【dll修复程序.site  】进入修复程序站点点击修复

 4、下载安装之后点击开始修复dll文件缺失，等待自动修复完成即可解决

解决方法二

如果你有其他电脑上有msvcr120.dll文件，你可以将它复制到你的电脑上。你需要将这个文件复制到以下目录：C:\Windows（但是你要确定你电脑的系统是多少位系统才可以）。

执行系统还原，将计算机还原到某个较早的日期，前提是你必须在发生错误之前创建了系统还原点。

 

解决方法三

重启一下电脑计算机，有时候重启一下电脑也可以解决这个问题

从Microsoft官方网站上下载msvcr120.dll系统文件，并按照提示进行安装。请注意安装程序必须知道自己计算机系统的架构匹配（32位系统安装x86版本，64位系统安装x64版本）。

 以上是解决电脑提示msvcr120.dll丢失的几种方法，如果你遇到了这个问题，可以使用以上方法解决。