（一）杭电原题

Tian Ji -- The Horse Racing

Problem Description

Here is a famous story in Chinese history.

"That was about 2300 years ago. General Tian Ji was a high official in the country Qi. He likes to play horse racing with the king and others."

"Both of Tian and the king have three horses in different classes, namely, regular, plus, and super. The rule is to have three rounds in a match; each of the horses must be used in one round. The winner of a single round takes two hundred silver dollars from the loser."

"Being the most powerful man in the country, the king has so nice horses that in each class his horse is better than Tian's. As a result, each time the king takes six hundred silver dollars from Tian."

"Tian Ji was not happy about that, until he met Sun Bin, one of the most famous generals in Chinese history. Using a little trick due to Sun, Tian Ji brought home two hundred silver dollars and such a grace in the next match."

"It was a rather simple trick. Using his regular class horse race against the super class from the king, they will certainly lose that round. But then his plus beat the king's regular, and his super beat the king's plus. What a simple trick. And how do you think of Tian Ji, the high ranked official in China?"

Were Tian Ji lives in nowadays, he will certainly laugh at himself. Even more, were he sitting in the ACM contest right now, he may discover that the horse racing problem can be simply viewed as finding the maximum matching in a bipartite graph. Draw Tian's horses on one side, and the king's horses on the other. Whenever one of Tian's horses can beat one from the king, we draw an edge between them, meaning we wish to establish this pair. Then, the problem of winning as many rounds as possible is just to find the maximum matching in this graph. If there are ties, the problem becomes more complicated, he needs to assign weights 0, 1, or -1 to all the possible edges, and find a maximum weighted perfect matching...

However, the horse racing problem is a very special case of bipartite matching. The graph is decided by the speed of the horses --- a vertex of higher speed always beat a vertex of lower speed. In this case, the weighted bipartite matching algorithm is a too advanced tool to deal with the problem.

In this problem, you are asked to write a program to solve this special case of matching problem.

Input

The input consists of up to 50 test cases. Each case starts with a positive integer n (n <= 1000) on the first line, which is the number of horses on each side. The next n integers on the second line are the speeds of Tian’s horses. Then the next n integers on the third line are the speeds of the king’s horses. The input ends with a line that has a single 0 after the last test case.

Output

For each input case, output a line containing a single number, which is the maximum money Tian Ji will get, in silver dollars.

Sample Input

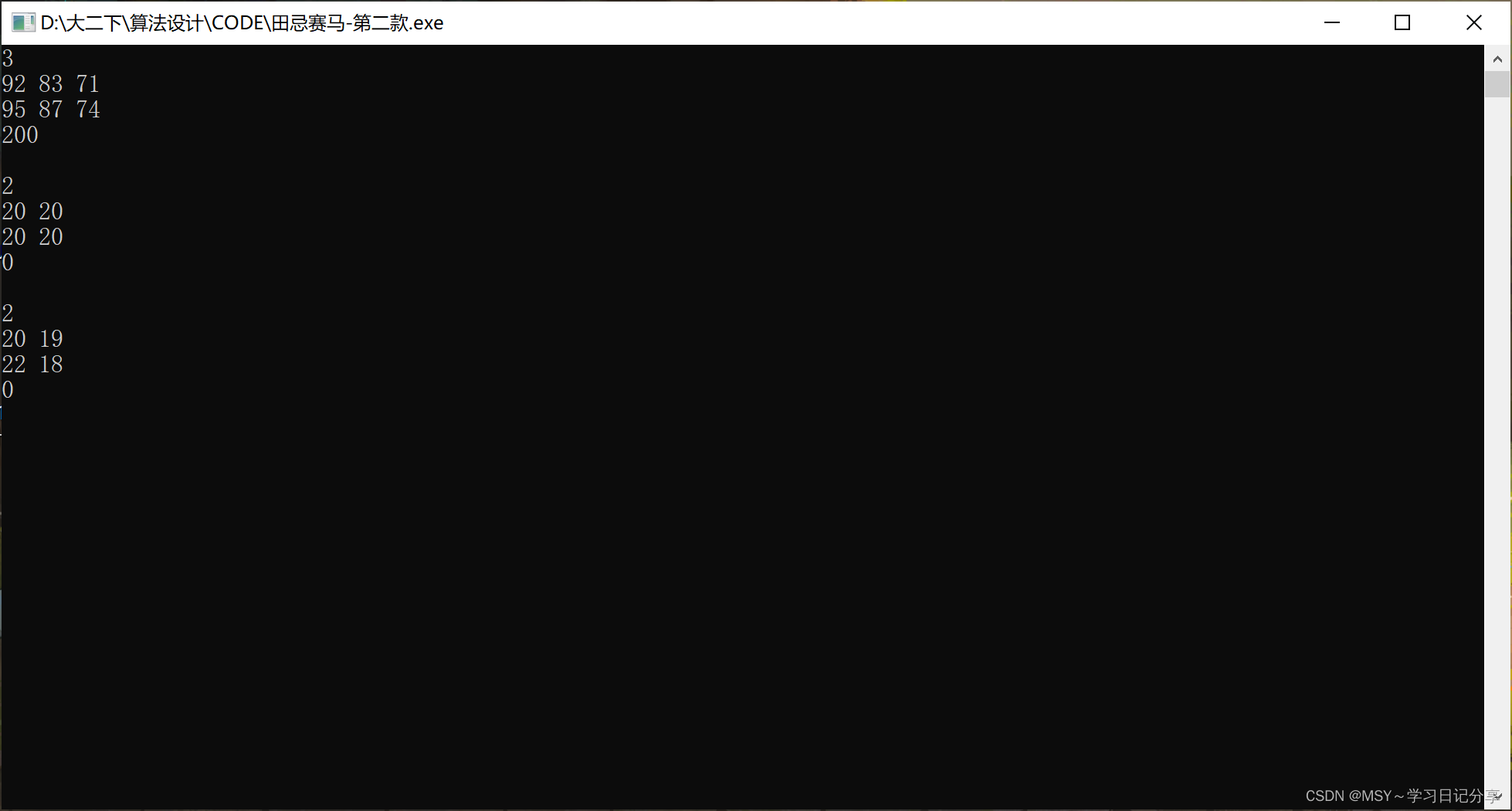
3

92 83 71

95 87 74

2

20 20

20 20

2

20 19

22 18

0

Sample Output

200

0

0

Source

2004 Asia Regional Shanghai

（二）Please speak Chinese:

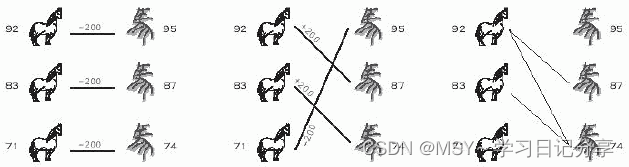
田忌赛马问题：

田忌和齐王赛马,两人各出 n 匹马,赢一场比赛得 200 两银子,输了赔 200 银子,平局不赔不赚. 已知两人每匹马的速度,问田忌最多能赢多少银子. 多组测试数据, 每组数据的第一行是一个整数 n。 (1<=n<=1000) 第二行包括 n 个整数既田忌每匹马的速度. 第三行包括 n 个整数既齐王每匹马的速度. 每匹马的速度不超过 1000. 对于每组数据输出一行有一个整数代表田忌最多能赢多少银子？

（三）手写草稿+理解思路+核心算法

第一款代码：

#include<bits/stdc++.h>

using namespace std;
int cmp(int a,int b){
    return a>b;
}//sort排序
int a[10000],b[10000];
int main(){
    int n,fa,fb,la,lb,cnt;
    while(cin>>n&&n!=0){
        for(int i=1;i<=n;i++){
            cin>>a[i];
        }//读入田忌的马
        for(int i=1;i<=n;i++){
            cin>>b[i];
        }//读入齐王的马
        sort(a+1,a+n+1,cmp);
        sort(b+1,b+n+1,cmp);
        fa=1;
        la=n;
        fb=1;
        lb=n;//赋值最快最慢的马
        cnt=0;
    for(int i=1;i<=n;i++){
    if(a[fa]>b[fb]){
        cnt++;
        fa++;
        fb++;//(在数组里通过移动此变量的位置来实现当前最快最慢的马的赋值)
    }else if(a[la]>b[lb]){
        cnt++;
        la--;
        lb--;
    }else{
        if(a[la]<b[fb]){
            cnt--;
            la--;
            fb++;
        }
    }
}
cout<<cnt*200<<endl;
}
    return 0;
}

第二款代码：

这个代码写出来后，发现有一个小bug，输出结果第三种是错误的，应该为平局，实际却是200，感兴趣的伙伴可以找一下问题所在。

#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#define MAX_N 1000
int tian[MAX_N]; // 田忌的马的速度
int qi[MAX_N]; // 齐王的马的速度
int cmp(const void *a, const void *b) {
    return *(int *)a - *(int *)b;
}
int main() {
    int n;
    while (scanf("%d", &n) != EOF) {
        int i;
        for (i = 0; i < n; i++) {
            scanf("%d", &tian[i]);
        }
        for (i = 0; i < n; i++) {
            scanf("%d", &qi[i]);
        }
        qsort(tian, n, sizeof(int), cmp);
        qsort(qi, n, sizeof(int), cmp);
        int tian_head = 0, tian_tail = n - 1, qi_head = 0, qi_tail = n - 1;
        int ans = 0;
        while (tian_head <= tian_tail) {
            if (tian[tian_head] > qi[qi_head]) {
                ans += 200;
                tian_head++;
                qi_head++;
            } else if (tian[tian_tail] > qi[qi_tail]) {
                ans += 200;
                tian_tail--;
                qi_tail--;
            } else {
                if (tian[tian_tail] > qi[qi_head]) {
                    ans += 200;
                }
                tian_tail--;
                qi_head++;
            }
        }
        printf("%d\n", ans);
    }
    return 0;
}