在训练模型的时候，我们需要将损失函数一直训练到0吗？显然不用。一般来说，我们是用训练集来训练模型，但希望的是验证机的损失越小越好，而正常来说训练集的损失降到一定值后，验证集的损失就会开始上升，因此没必要把训练集的损失降低到0

既然如此，在已经达到了某个阈值之后，我们可不可以做点别的事情来提升模型性能呢？ICML2020的论文《Do We Need Zero Training Loss After Achieving Zero Training Error?》回答了这个问题，不过实际上它并没有很好的描述"为什么"，而只是提出了"怎么做"

思路描述

论文提供的解决方案非常简单，假设原来的损失函数是$\mathcal{L}(\theta )$，现在改为$\tilde{\mathcal{L}}(\theta )$：
$$\tilde{\mathcal{L}}(\theta )=|\mathcal{L}(\theta )-b|+b\text{\hspace{1em}(1)}$$
其中$b$是预先设定的阈值。当$\mathcal{L}(\theta )>b$时$\tilde{\mathcal{L}}(\theta )=\mathcal{L}(\theta )$，这时就是执行普通的梯度下降；而$\mathcal{L}(\theta )<b$时$\tilde{\mathcal{L}}(\theta )=2b-\mathcal{L}(\theta )$，注意到损失函数变号了，所以这时候是梯度上升。因此，总的来说就是以$b$为阈值，低于阈值时反而希望损失函数变大。论文把这个改动称为**“Flooding”**

这样做有什么效果呢？论文显示，在某些任务中，训练集的损失函数经过这样处理后，验证集的损失能出现"二次下降（Double Descent）"，如下图

左图：不加Flooding的训练示意图；右图：加了Flooding的训练示意图

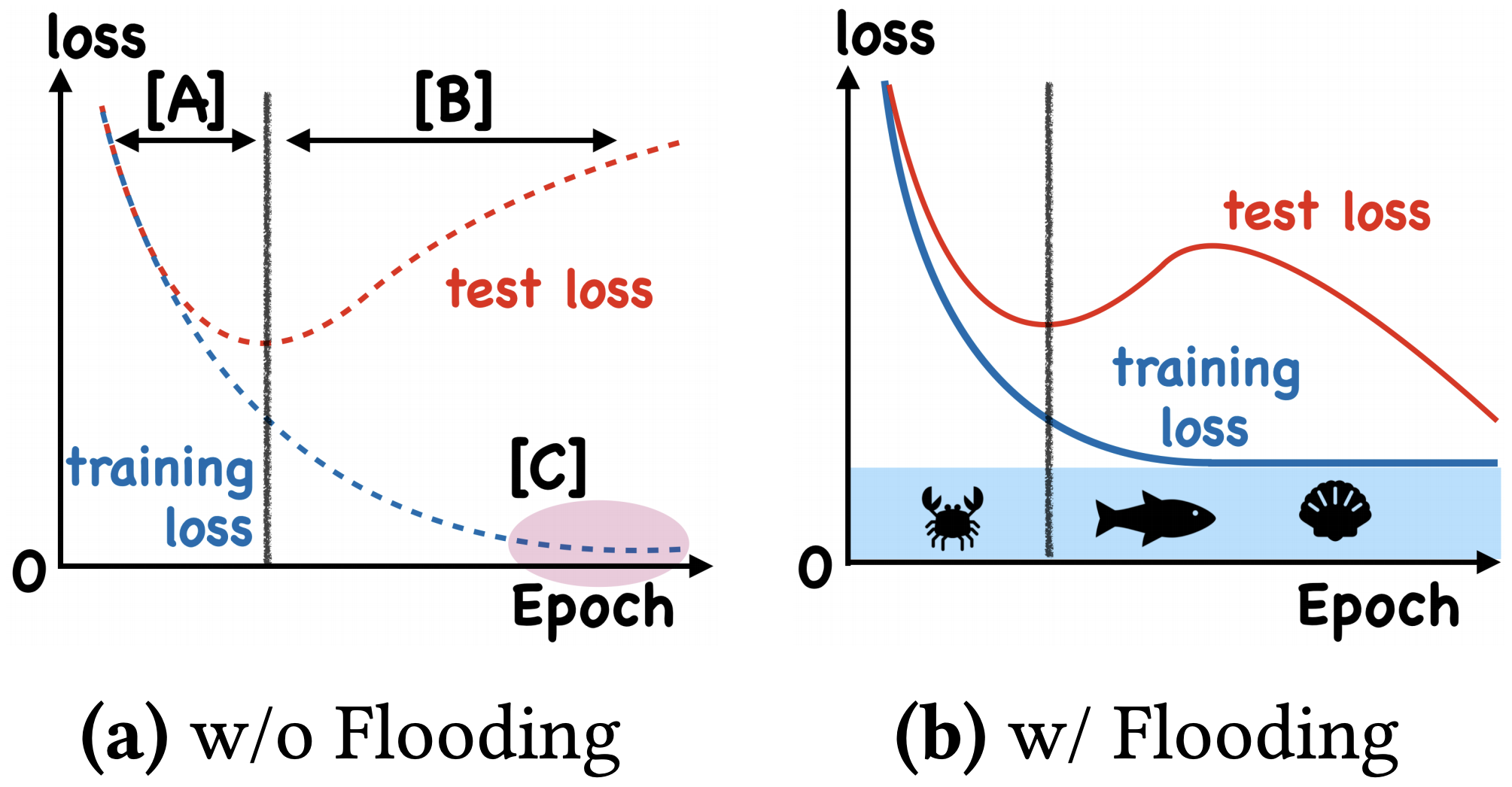
简单来说，就是最终的验证集效果可能更好一些，原论文的实验结果如下：

Flooding的实验结果：第一行W表示是否使用weight decay，第二行E表示是否使用early stop，第三行的F表示是否使用Flooding

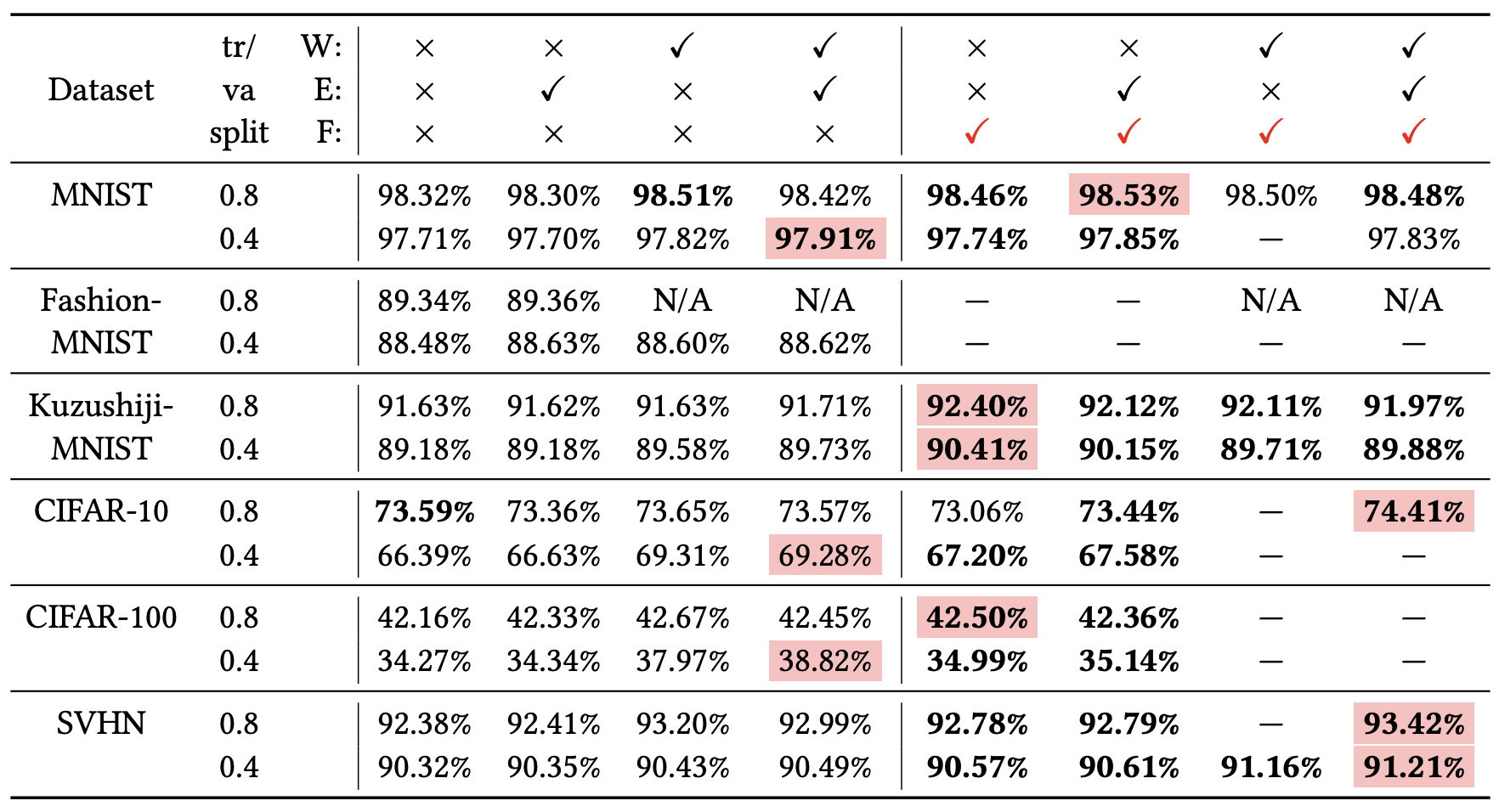
个人分析

如何解释这个方法呢？可以想像，当损失函数达到$b$之后，训练流程大概就是在交替执行梯度下降和梯度上升。直观想的话，感觉一步上升一步下降，似乎刚好抵消了。事实真的如此吗？我们来算一下看看。假设先下降一步后上升一步，学习率为$\epsilon$，那么：
$$\begin{array}{rl}& {\theta }_n={\theta }_{n-1}-\epsilon g({\theta }_{n-1})\\ & {\theta }_{n+1}={\theta }_n+\epsilon g({\theta }_n)\end{array}\text{\hspace{1em}(2)}$$
其中$g(\theta )={\nabla }_{\theta }\mathcal{L}(\theta )$，现在我们有
$$\begin{array}{rl}{\theta }_{n+1}=& {\theta }_{n-1}-\epsilon g({\theta }_{n-1})+\epsilon g({\theta }_{n-1}-\epsilon g({\theta }_{n-1}))\\ \approx & {\theta }_{n-1}-\epsilon g({\theta }_{n-1})+\epsilon (g({\theta }_{n-1})-\epsilon {\nabla }_{\theta }g({\theta }_{n-1})g({\theta }_{n-1}))\\ =& {\theta }_{n-1}-\frac{{\epsilon }^2}{2}{\nabla }_{\theta }\Vert g({\theta }_{n-1}){\Vert }^2\end{array}\text{\hspace{1em}(3)}$$

近似那一步实际上是使用了泰勒展开，我们将${\theta }_{n-1}$看作$x$，$\epsilon g({\theta }_{n-1})$看作$\Delta x$，由于
$$\frac{g(x-\Delta x)-g(x)}{-\Delta x}={\nabla }_{x}g(x)$$
所以
$$g(x-\Delta x)=g(x)-\Delta x{\nabla }_{x}g(x)$$

最终的结果就是相当于学习率为$\frac{{\epsilon }^2}{2}$、损失函数为梯度惩罚$\Vert g(\theta ){\Vert }^2=\Vert {\nabla }_{\theta }\mathcal{L}(\theta ){\Vert }^2$的梯度下降。更妙的是，改为"先上升再下降"，其表达式依然是一样的（这不禁让我想起"先涨价10%再降价10%“和"先降价10%再涨价10%的故事”）。因此，平均而言，Flooding对损失函数的改动，相当于在保证了损失函数足够小之后去最小化$\Vert {\nabla }_x\mathcal{L}(\theta ){\Vert }^2$，也就是推动参数往更平稳的区域走，这通常能提高泛化性（更好地抵抗扰动），因此一定程度上就能解释Flooding有作用的原因了

本质上来讲，这跟往参数里边加入随机扰动、对抗训练等也没什么差别，只不过这里是保证了损失足够小后再加扰动

继续脑洞

想要使用Flooding非常简单，只需要在原有代码基础上增加一行即可

logits = model(x)
loss = criterion(logits, y)
loss = (loss - b).abs() + b # This is it!
optimizer.zero_grad()
loss.backward()
optimizer.step()

有心是用这个方法的读者可能会纠结于$b$的选择，原论文说$b$的选择是一个暴力迭代的过程，需要多次尝试

The flood level is chosen from b ∈ { 0 , 0.01 , 0.02 , . . . , 0.50 } b\in \{0, 0.01,0.02,...,0.50\} b∈{0,0.01,0.02,...,0.50}

不过笔者倒是有另外一个脑洞：$b$无非就是决定什么时候开始交替训练罢了，那如果我们从一开始就用不同的学习率进行交替训练呢？也就是自始自终都执行
$$\begin{array}{rl}& {\theta }_n={\theta }_{n-1}-{\epsilon }_{1}g({\theta }_{n-1})\\ & {\theta }_{n+1}={\theta }_n+{\epsilon }_{2}g({\theta }_n)\end{array}\text{\hspace{1em}(4)}$$
其中${\epsilon }_1>{\epsilon }_2$，这样我们就把$b$去掉了（引入了${\epsilon }_1,{\epsilon }_2$的选择，天下没有免费的午餐）。重复上述近似展开，我们就得到
$$\begin{array}{rl}{\theta }_{n+1}=& {\theta }_{n-1}-{\epsilon }_{1}g({\theta }_{n-1})+{\epsilon }_{2}g({\theta }_{n-1}-{\epsilon }_{1}g({\theta }_{n-1}))\\ \approx & {\theta }_{n-1}-{\epsilon }_{1}g({\theta }_{n-1})+{\epsilon }_2(g({\theta }_{n-1})-{\epsilon }_1{\nabla }_{\theta }g({\theta }_{n-1})g({\theta }_{n-1}))\\ =& {\theta }_{n-1}-({\epsilon }_1-{\epsilon }_2)g({\theta }_{n-1})-\frac{{\epsilon }_1{\epsilon }_2}{2}{\nabla }_{\theta }\Vert g({\theta }_{n-1}){\Vert }^2\\ =& {\theta }_{n-1}-({\epsilon }_1-{\epsilon }_2){\nabla }_{\theta }\left[\mathcal{L}({\theta }_{n-1})+\frac{{\epsilon }_1{\epsilon }_2}{2({\epsilon }_1-{\epsilon }_2)}\Vert {\nabla }_{\theta }\mathcal{L}({\theta }_{n-1}){\Vert }^2\right]\end{array}\text{\hspace{1em}(5)}$$
这就相当于自始自终都在用学习率${\epsilon }_1-{\epsilon }_2$来优化损失函数$\mathcal{L}(\theta )+\frac{{\epsilon }_1{\epsilon }_2}{2({\epsilon }_1-{\epsilon }_2)}\Vert {\nabla }_{\theta }\mathcal{L}(\theta ){\Vert }^2$了，也就是说一开始就把梯度惩罚给加了进去，这样能提升模型的泛化性能吗？《Backstitch: Counteracting Finite-sample Bias via Negative Steps》里边指出这种做法在语音识别上是有效的，请读者自行测试甄别

效果检验

我随便在网上找了个竞赛，然后利用别人提供的以BERT为baseline的代码，对Flooding的效果进行了测试，下图分别是没有做Flooding和参数$b=0.7$的Flooding损失值变化图，值得一提的是，没有做Flooding的验证集最低损失值为0.814198，而做了Flooding的验证集最低损失值为0.809810

根据知乎文章一行代码发一篇ICML？底下用户Curry评论所言：“通常来说$b$值需要设置成比’Validation Error开始上升’的值更小，1/2处甚至更小，结果更优”，所以我仔细观察了下没有加Flooding模型损失值变化图，大概在loss为0.75到1.0左右的时候开始出现过拟合现象，因此我又分别设置了$b=0.4$和$b=0.5$，做了两次Flooding实验，结果如下图

值得一提的是，$b=0.4$和$b=0.5$时，验证集上的损失值最低仅为0.809958和0.796819，而且很明显验证集损失的整体上升趋势更加缓慢。接下来我做了一个实验，主要是验证"继续脑洞"部分以不同的学习率一开始就交替着做梯度下降和梯度上升的效果，其中，梯度下降的学习率我设为$1e-5$，梯度上升的学习率为$1e-6$，结果如下图，验证集的损失最低仅有0.783370

References

• 我们真的需要把训练集的损失降低到零吗？
• 一行代码发一篇ICML？