实现：

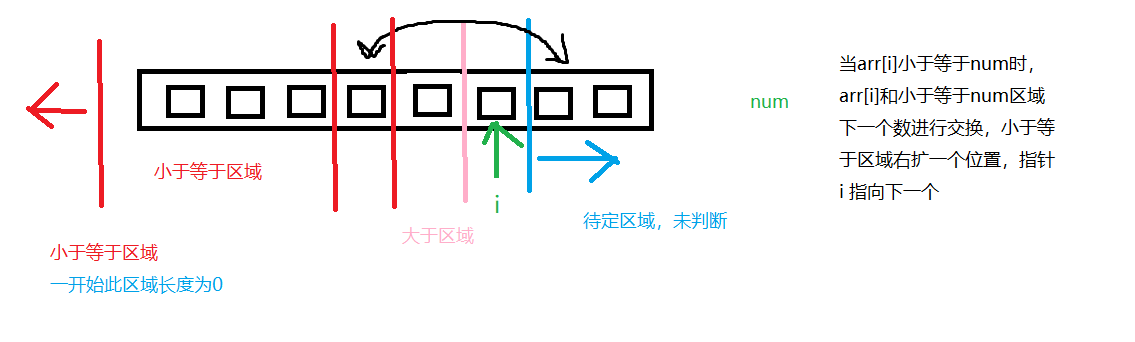
当arr[i]小于等于num时，arr[i]和小于等于num区域下一个数进行交换，小于等于区域右扩一个位置，指针 i 指向下一个

当arr[i]大于num时，指针 i 指向下一个

指针 i 越界时完成

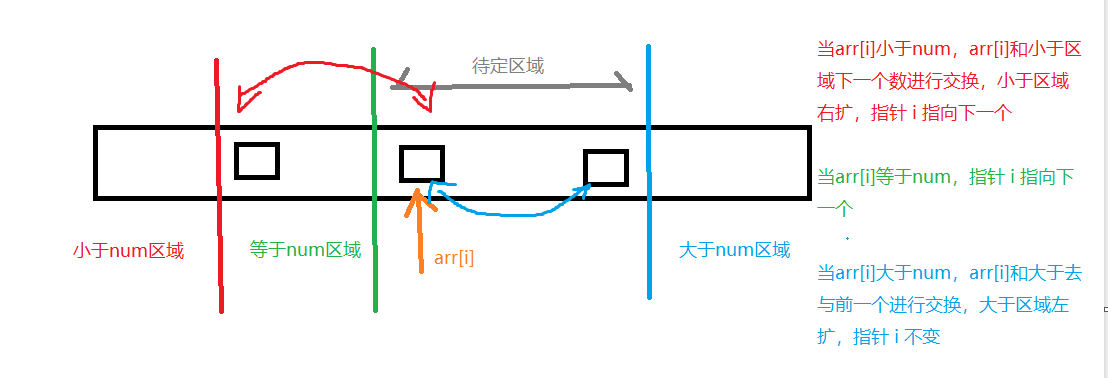
升级版本：将小于、等于、大于三个区域分开

实现：

当arr[i]小于num，arr[i]和小于区域下一个数进行交换，小于区域右扩，指针 i 指向下一个

当arr[i]等于num，指针 i 指向下一个

当arr[i]大于num，arr[i]和大于去与前一个进行交换，大于区域左扩，指针 i 不变

等于区域与大于区域相遇时完成

 

快速排序1.0

在数组中，将最后一位数作num，除却最后一位数的数组实现小于等于num区域和大于num区域划分，将num与小于等于num区域的后一位数交换，此时num这个数排序完成

以num这个数为分界点，左侧和右侧的数组重复进行此操作

快速排序2.0   

一次搞定一批数

在数组中，将最后一位数作num，除却最后一位数的数组实现小于num区域，等于num区域和大于num区域划分，将num与等于num区域的后一位数交换，此时num这个数排序完成

以等于num区域为分界点，左侧和右侧的数组重复进行此操作

快速排序的不稳定性

快排的时间复杂度取决于取到的num的值在数组中的大小；

如果num取的数极大或极小时，排序的时间复杂度趋向于O(N^2)

如果num取的数较为中间，排序的时间复杂度趋向于O(NlogN)

快速排序3.0

随机选一个数，与最后一个数进行交换，取这个数作为num

此时取到的num的值为概率事件，排序的时间复杂度也为概率事件

最终代码

package algorithm;

import org.junit.Test;

public class QuickSort {
    @Test
    public void test() {
        int[] arr = new int[]{2, 1};
        quickSort(arr);
        for (int i:arr) {
            System.out.println(i);
        }
    }

    public static void quickSort(int[] arr) {
        if (arr == null || arr.length == 0) {
            return;
        }
        quickSort(arr, 0, arr.length - 1);
    }

    //arr[L]到arr[R]区域排序
    public static void quickSort(int[] arr, int L, int R) {
        if (L < R) {
            swap(arr, (int) (L + Math.random() * (R - L + 1)), R);//随机一个数和最后一个数进行交换, 作为num
            int[] p = partiion(arr, L, R);//获取等于num区域
            quickSort(arr, L, p[0] - 1);//小于区域
            quickSort(arr, p[1] + 1, R);//大于区域
        }
    }

    //num = arr[R]
    public static int[] partiion(int[] arr, int L, int R) {
        int less = L - 1;//小于区域右边界
        int more = R;//大于区域左边界
        while (L < more) { //L表示当前位置, 为什么是L呢，因为i也是从数组开头走的
            if (arr[L] < arr[R]) {//当前的数小于num
                swap(arr, ++less, L++);//less后一个数和arr[L]交换，指针L右移一位
            } else if (arr[L] > arr[R]) {
                swap(arr, --more, L);//more前一个数和arr[L]交换，指针L不变
            } else {
                L++;
            }
        }
        swap(arr, more, R);//num和大于区域左边界，等于区域的后一位数交换
        return new int[]{less + 1, more};//输出等于num区域
    }

    public static void swap(int[] arr, int a, int b) {
        int temp = arr[a];
        arr[a] = arr[b];
        arr[b] = temp;
    }
}