一.选择题:
1.A 派生出子类 B , B 派生出子类 C ,并且在 java 源代码有如下声明:
1. A a0=new A();
2. A a1=new B();
3. A a2=new C();
问以下哪个说法是正确的()A 只有第一行能通过编译
B 第1、2行能通过编译,但第3行编译出错
C 第1、2、3行能通过编译,但第2、3行运行时出错
D 第1行,第2行和第3行的声明都是正确的
答案:D
分析:我们知道,以上三种声明都内含了三者的默认构造方法,因此当然可以编译通过。但看问题要看重点,此题我们引出另一个问题:
java的编译是什么?
这个问题其实对于 java 语言而言是可以不计较的,因为 java 作为跨平台性极好的语言,其底层逻辑大都由JVM虚拟机实现了,但此处理解编译的过程更有助于我们理解原理;
java 的编译过程分为两部分:前端编译和后端编译;
- 前端编译:就是把java 源码转化为 .class 的字节码文件,但这样的文件机器还不能读懂;
- 后端编译:再把字节码文件通过JVM虚拟机加载后翻译层机器码,这样机器就能根据指令去执行了
通常所说的能否编译成功到底是什么意思?
这里主要针对本题类型的类,经常有题型问会不会编译失败?我们可以仔细思考一下到底什么叫“编译失败”?——失败可能是因为“类初始化”,也可能因为“类加载过程”;
类初始化过程:
- 初始化父类中的静态成员变量和静态代码块;
- 初始化子类中的静态成员变量和静态代码块;
- 初始化父类的普通成员变量和代码块,再执行父类的构造方法;
- 初始化子类的普通成员变量和代码块,再执行子类的构造方法;
既然是针对类的,那么不得不提“JVM 类加载过程”了(了解即可);
其实对于一个类,它的生命周期可以用这样的五步描述:
[加载] →[连接]:(验证)→ (准备)→ (解析) → [初始化] → [使用] →[卸载]
2.
下面代码将输出什么内容:()public class SystemUtil{
public static boolean isAdmin(String userId){
return userId.toLowerCase()=="admin";
}
public static void main(String[] args){
System.out.println(isAdmin("Admin"));
}
}A true
B false
C 1
D 编译错误
答案:B
分析:看这道题之前可以先看一下这道题的扩展,猜猜看以下代码的结果?

结果如下:

解释:其实直接原因在 toLowerCase() 方法,但根本原因在存储位置;
先来看 toLowerCase() 方法的问题:进入其内部源码,可以看到,如果原本的字符串是小写,就返回当前字符串的 this 对象,如果是大写,就经过一系列转换后变成小写,再new一个新的 String 对象接收后返回:
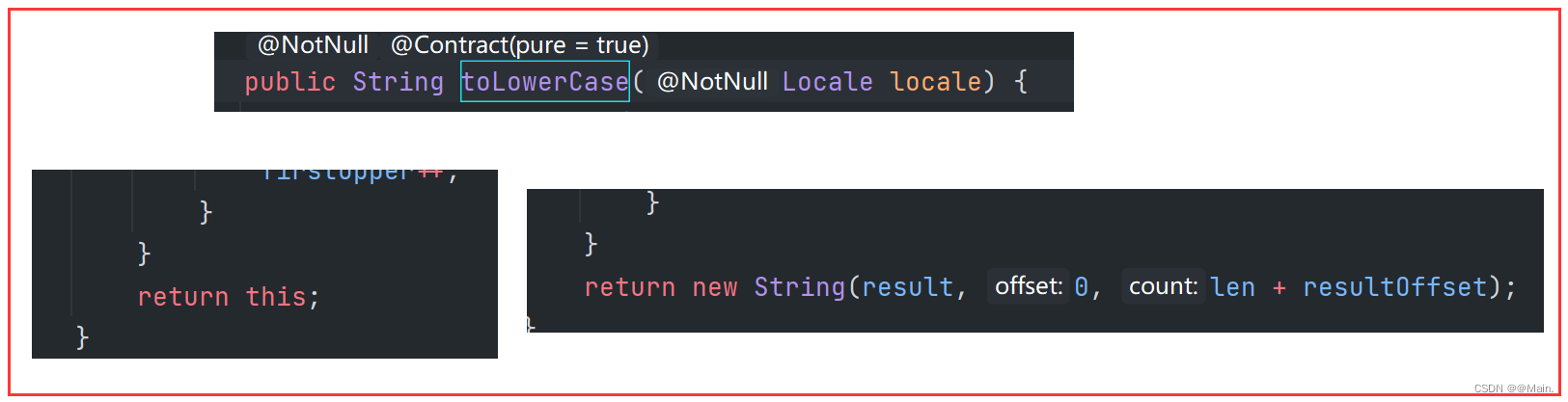
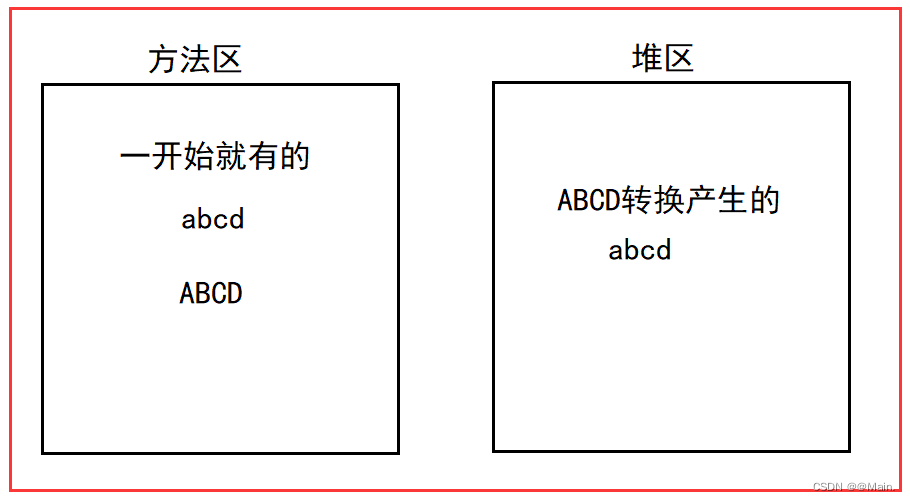
接着看根本原因:存储位置不同;
java源码被编译为class文件后还要加载到内存中的运行时数据区,交给命令解析器解析成机器码,在上面这段代码中,一开始就有的“abcd”、“ABCD”都是字面值保存在“字符串常量池”中,其跟随类在加载时就存入到class文件中,之后随着运行期进入方法区;我们又知道,凡是 new 出来对象的都放在堆区,那么它们什么时候一样什么时候不一样就显而易见了;
6.
如下代码的输出结果是什么?
public class Test {
public int aMethod(){
static int i = 0;
i++;
return i;
}
public static void main(String args[]){
Test test = new Test();
test.aMethod();
int j = test.aMethod();
System.out.println(j);
}
}A 0
B 1
C 2
D 编译失败
答案:D
分析:static 修饰的成员是属于类的,因此修饰普通成员变量时只能放在类里面,不能放在普通方法里面,否则就是属于方法的了。
9.
选项中哪一行代码可以替换 //add code here 而不产生编译错误
public abstract class MyClass {
public int constInt = 5;
//add code here
public void method() {
}
}A public abstract void method(int a);
B consInt=constInt+5;
C public int method();
D public abstract void anotherMethod(){}
答案:A
分析:A 是声明了一个抽象方法,当然没问题,刚好和下面的 method() 方法构成重载;
B 这种要注意:所有对成员变量做赋值、计算的操作都要放在方法内部;
C 这个方法既然不是抽象方法就不能这样去声明,必须有{}来进行body的实现;
D 这样的抽象方法只能声明不能自行具体实现;
二.编程题:
链接:排序子序列_牛客笔试题_牛客网
来源:牛客网牛牛定义排序子序列为一个数组中一段连续的子序列,并且这段子序列是非递增或者非递减排序的。牛牛有一个长度为n的整数数组A,他现在有一个任务是把数组A分为若干段排序子序列,牛牛想知道他最少可以把这个数组分为几段排序子序列.
如样例所示,牛牛可以把数组A划分为[1,2,3]和[2,2,1]两个排序子序列,至少需要划分为2个排序子序列,所以输出2输入描述:
输入的第一行为一个正整数n(1 ≤ n ≤ 10^5) 第二行包括n个整数A_i(1 ≤ A_i ≤ 10^9),表示数组A的每个数字。输出描述:
输出一个整数表示牛牛可以将A最少划分为多少段排序子序列示例1
输入
6 1 2 3 2 2 1输出
2
分析:遍历整个序列,每次序列改变就会组数加1,当遇到当前数和下一个数的大小关系不符合之前的关系时,就会导致序列改变;
分为三种情况:①num[i] < num[i+1]、②num[i] > num[i+1]、③num[i] == num[i+1];
相等属于序列不变,不相等时,让索引 i 向后走一步,进入下一组,同时组数加1即可;
注意点:数组越界问题
如果遇到最后一个数时序列改变了,那么就要考虑越界问题,所以就可以在开辟数组时多开一个大小,存放一个0,解决了越界还不影响分组;

public class Test100448 {
public static void main(String[] args) {
Scanner scan = new Scanner(System.in);
int n = scan.nextInt();
int[] num = new int[n + 1];
for (int i = 0; i < n; i++) {
num[i] = scan.nextInt();
}
System.out.println(subGroups(num));
}
private static int subGroups(int[] num) {
int groups = 0;
int i = 0;
while (i < num.length - 1) {
if (num[i] < num[i+1]) {
// 当前为递增序列
while (i < num.length - 1 && num[i] < num[i+1]) {
i++;
}
groups++;
i++;
} else if (num[i] == num[i+1]) {
// 前后相等
i++;
} else {
// 当前为递减序列
while (i < num.length - 1 && num[i] > num[i+1]) {
i++;
}
groups++;
i++;
}
}
return groups;
}
}链接:倒置字符串_牛客题霸_牛客网
描述
将一句话的单词进行倒置,标点不倒置。比如 I like beijing. 经过函数后变为:beijing. like I
输入描述:
每个测试输入包含1个测试用例: I like beijing. 输入用例长度不超过100
输出描述:
依次输出倒置之后的字符串,以空格分割
示例1
输入:
I like beijing.复制输出:
beijing. like I
分析:此题比较简单,可以先把整个字符串逆置,再把内部的每个单词逆置就可以了。
逆置内部单词时,以空格为分界,但要注意,万一整个字符串里没有空格呢?这种情况要防止数组越界;
除了这种方法,还可以想到:先用队列把每个单词存起来,再使用栈把每个队列存起来,最后依次弹出栈顶的队列,再依次出队列,就能得到想要的顺序了。
public class Test69389 {
public static void main(String[] args) {
Scanner scan = new Scanner(System.in);
String s = scan.nextLine();
char[] src = s.toCharArray();
String ret = new String(stringVerse(src));
System.out.println(ret);
}
private static char[] stringVerse(char[] src) {
// 先将整个字符串全部逆置
subVerse(src,0,src.length - 1);
// 再将每个单词逆置
int i = 0;
while (i < src.length){
int cur = i;
while (cur < src.length && src[cur] != ' ') {
cur++;
}
// 判断中间是否有空格
if (cur < src.length) {
subVerse(src,i,cur-1);
i = cur + 1;
} else {
subVerse(src,i,cur-1);
i = cur;
}
}
return src;
}
private static void subVerse(char[] src, int start, int end) {
while (start <= end) {
char temp = src[end];
src[end] = src[start];
src[start] = temp;
++start;
--end;
}
}
}